数学Ⅰの最後に学習するのが『データの分析』ですね。
今回解決する悩み
「データの単元が苦手」
「データの分析を総復習したい」
今回はデータの分析に関するこんな悩みを解決します。
 高校生
高校生
データの分析の重要公式が総復習できる完全攻略記事を書きました。
※本ページは学習アプリのプロモーションが含まれています。



ぜひ最後までご覧ください。
度数分布表
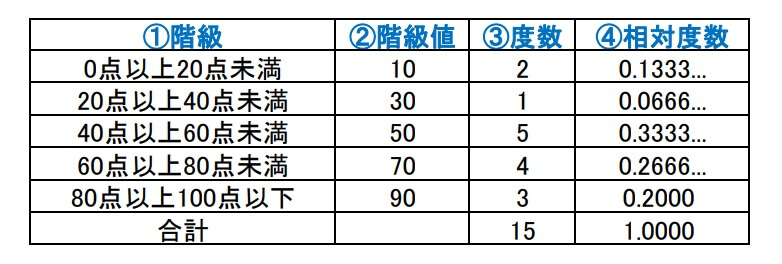

度数分布表とは「データを階級ごとに分けて分布を表した表」です。
用語の解説
②階級値:各階級の真ん中の値を階級値といいます。たとえば「20点以上40点未満」の階級の階級値は30です。
③度数:その階級に含まれるデータの個数を表します。
④相対度数:全体の度数に対して、その階級に属する度数の割合
⑤階級の幅:階級の広さを指します。この度数分布表では20点ごとに区切っているので階級の幅は20です。
データを度数分布表にすることでデータ全体の分布が掴みやすくなります。
例えば以下のようなデータがあるとき、点数の分布はいまいち分かりません。
テスト結果
82 63 91 46 53 7 37 97 15 44 66 74 59 53 62 (点)
そこでテストの点数を一定の幅で分けて、以下のようにしたものが度数分布表です。
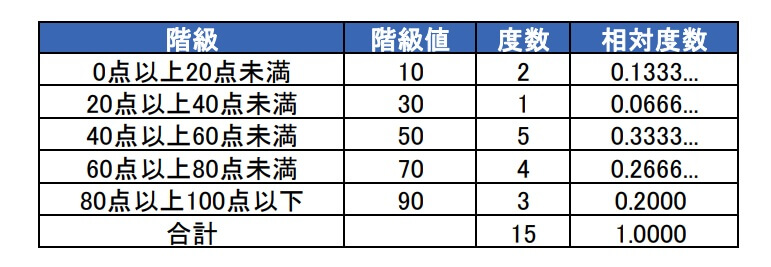

度数分布表の各値の求め方は「度数分布表とは?平均値・最頻値の求め方を解説!」で解説しています。


ヒストグラム
ヒストグラムとは「データを階級ごとに表した棒グラフ」です。
度数分布表を元にしてヒストグラムを作ったのが下の図です。
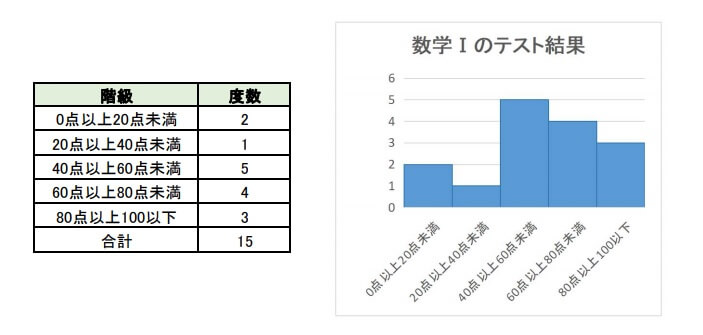

左の度数分布表をもとにして、右のヒストグラムを作成しました。
ヒストグラムの書き方
ヒストグラムの書き方について解説します。
ここに英語のテスト結果があります。
テスト結果
82 63 91 46 53 7 37 35 26 44 66 74 59 53 38 (点)
このままではデータの分布が分かりづらいので階級ごとに分け、度数分布表にまとめます。
度数分布表で表したものが下の表です。
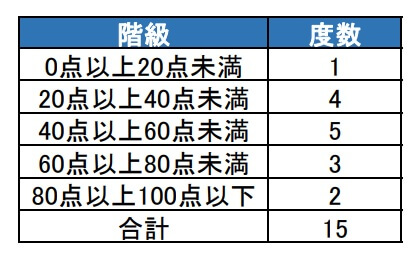

これでデータを整理できたのでヒストグラムにしていきます。
横軸には階級を書き入れましょう。

そして縦軸を度数(人数)にして、棒グラフで表します。
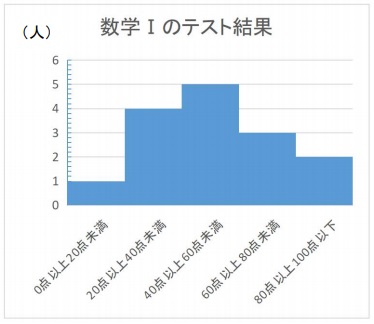

これでヒストグラムの完成です。
ヒストグラムについては「 ヒストグラムの書き方と平均値・中央値の求め方を解説!」で詳しく解説しています。


データの代表値
データ全体の特徴を一つの値を表すものをデータの代表値といいます。
今回は代表値のなかでも、「平均値」,「最頻値」,「中央値」の3つを解説します。
覚えておきたい代表値
- 平均値
- 最頻値
- 中央値
平均値
代表値の中で1番身近なのが『平均値』だと思います。

全てのデータ値を足して、データの個数で割ると平均値が求められます。
つまり変数\(x\)の\(n\)個の値を\(x_1 ,x_2 ,\cdots,x_n\)とするとき、平均値\(\bar{x}\)は
\[\displaystyle \bar{x}=\frac{x_1 +x_2 +x_3 +…+x_n}{n}=\frac{1}{n}\sum_{k=0}^n x_k\]
で求めることができます。
式にすると少し難しいですが、やっていることは
- 全てのデータの値を足す
- 1で求めた値をデータの個数で割る
これで平均値を求めることができます。


中央値
データを大きさ順に並べ替えたときに中央にある値を『中央値』と呼びます。


データが偶数個なのか奇数個なのかによって、中央値の求め方が変わるので注意です。
中央値の求め方
データの個数が奇数個のときは簡単です。
なぜなら下図のように中央の値が1つに定まるため、ちょうど中央にある値が中央値となります。

しかし、データの個数が偶数の場合の中央値はどうでしょう。


中央を探すと2つの数字のあいだになってしまいました。
このようにデータが偶数個の場合は、中央に隣接する2つのデータの和を2で割った値が中央値となります。


中央値の求め方
データが奇数個のとき:大きさ順に並び替えて中央にくる値
データが偶数個のとき:大きさ順に並び替えて中央に隣接するデータの平均
中央値のメリット&デメリットについては「中央値(メジアン)とは?中央値の求め方とメリットを解説!」で解説しています。
とは?中央値の求め方とメリットを解説!-300x158.png)
とは?中央値の求め方とメリットを解説!-300x158.png)
最頻値
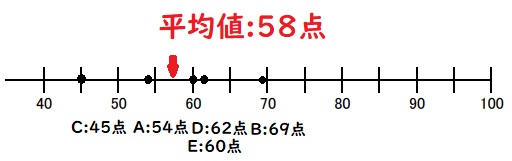
最頻値とは「もっとも登場回数が多い値」を指します。


上図の場合、”69″が最も多く登場しているため最頻値は69となります。
度数分布表の最頻値


度数分布表の最頻値は、「度数が最も高い階級の階級値」です。
参考
各階級の真ん中の値を「階級値」といいます。
例えば「20点以上40点未満」の階級の階級値は30です。
上の度数分布表で1番度数が大きいのは「40点以上60点未満」の階級です。
「40点以上60点未満」の階級値は50点なので、最頻値は50となります。
最頻値についてもっと詳しく知りたい方


データの四分位数
データの散らばりの様子を分布といいます。
データの分布が異なっていても、平均値や最頻値などが同じになることもあります。
データの範囲
データの範囲は「最大値と最小値の差」で求められます。
以下のデータにおいてデータの範囲は「25」です


データの最大値から最小値の差を求めたものが範囲です。


四分位数
データを大きさ順に並べたときに、4等分する位置の値を四分位数といいます。
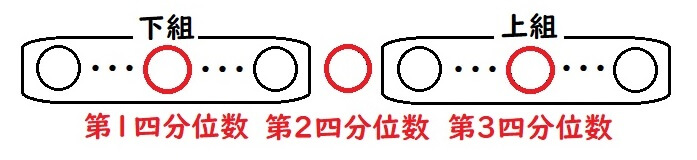

四分位数の求め方
四分位数の求め方を確認しましょう。
今回はデータが偶数個の場合を例に解説します。
四分位数の求め方
- データを大きさ順に並べる
- 中央値を求める
- 中央値を境に2等分する
- 下組の中央値,上組の中央値を求める
データが偶数個の場合は中央の2数の和を2で割ります。
.jpg)
.jpg)
四分位数はデータの個数の偶奇によって、求め方が少し変わります。
あまり自信がない方は「四分位数の求め方を解説」を参考にしてみてください。


四分位範囲・四分位偏差
四分位数における「第2四分位数と第3四分位数の差」が四分位範囲です。
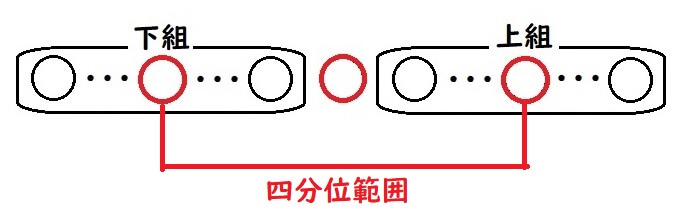

また、四分位範囲の半分を四分位偏差と呼びます。
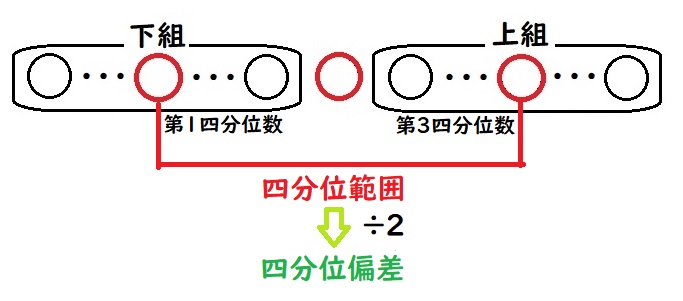

四分位範囲について詳しくはこちら
⇒四分位範囲と四分位偏差の意味と求め方


箱ひげ図
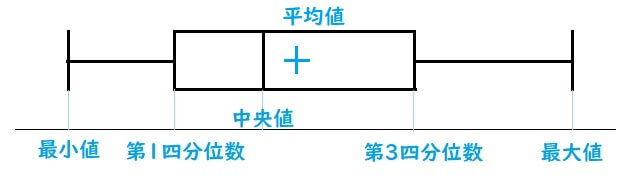

データの分析で意外と理解されていないのが箱ひげ図です。
箱ひげ図は「最小値」「最大値」「四分位数」「平均値」が分かる優れものです。
箱ひげ図の各線の見方を覚えておきましょう。
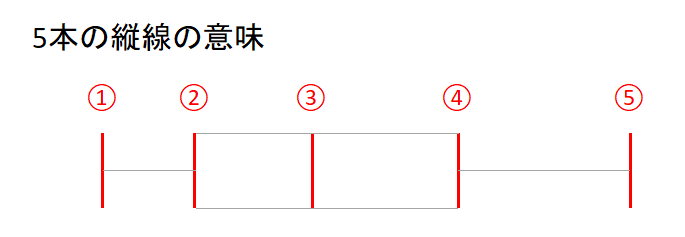

①の線\(\cdots\)最小値
②の線\(\cdots\)第1四分位数
③の線\(\cdots\)中央値
④の線\(\cdots\)第3四分位数
⑤の線\(\cdots\)最大値
箱ひげ図の書き方
箱ひげ図の書き方は以下の手順です
箱ひげ図の書き方
- データを大きさ順に並び替える
- 四分位数を求める
- 最大値・最小値・四分位数を書き込む
- 四分位数の箱を作る
- 最大値・最小値と箱をひげで結ぶ
箱ひげ図については別の記事でまとめました。


データの分散
四分位数からデータの分散の様子を読み取ることができました。
次はデータの値を用いて散らばりの度合いを表す分散について解説をします。
分散
分散は、データの散らばりの大きさを表す指標です。
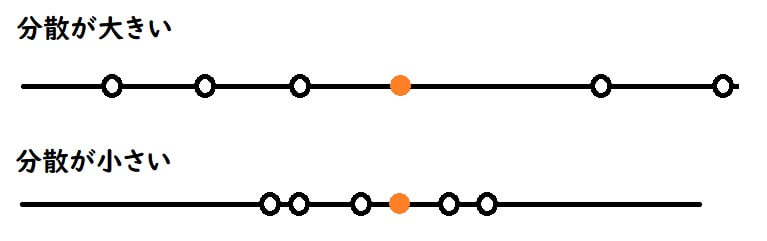

分散の大小によってデータ全体の分布をイメージすることができます。
分散の大小
分散が大きい⇒平均値から離れている値が多い
分散が小さい⇒平均値に近い値が多い
分散の求め方
分散は以下の公式で求めることができます。
分散の公式
変数\(x\)の値が\(x_1,x_2,…,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\begin{eqnarray}
s^{2}&=&\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+…+(x_{n}-\bar{x})^{2}\}[[
&=&\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}
\end{eqnarray}
もしくは
\[\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\]
分散が求められると標準偏差や相関係数を求めることができます。
標準偏差や相関係数もテストで出題されるので確認しておきましょう。
分散については別の記事で詳しく解説しました
分散とは?分散の公式と求め方を解説!標準偏差や共分散との違いは?


標準偏差


難しいと思われている標準偏差\(s\)ですが、分散\(s^{2}\)が分かれば簡単です。
まずはデータの値から分散を求めます。
分散の公式
変数\(x\)の値が\(x_1,x_2,…,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\begin{eqnarray}
s^{2}&=&\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+…+(x_{n}-\bar{x})^{2}\}[[
&=&\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}
\end{eqnarray}
もしくは
\[\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\]
そうして求めた分散の正の平方根が標準偏差です。
\[s=\sqrt{s^{2}}\]








データの相関係数
データには2つの数に相関関係がある場合があります。
相関関係があるとは、
一方が増加するときもう一方も増加傾向がある。
もしくは、一方が増加すとき他方は減少傾向にある。
このように2つのデータが連動して動く傾向があることを相関関係があるといいます。
共分散
共分散とは、「2組の対応するデータ間の関係を表す数値」です。
xとyの共分散\(s_{xy}\)は次の公式で求めます。
🔵共分散の公式①
共分散の公式①
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n (x_i -\overline{x})(y_i -\overline{y})\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
🔵共分散の公式②
共分散の公式②
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n x_i y_i – \overline{x} \overline{y}\]
すなわち
\[\displaystyle s_{xy}=\overline{xy}- \overline{x} \overline{y}\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
公式は少し難しいですが、共分散を求めるには大きく3つのステップです。
共分散の求め方①
- \(x, y\)の平均値を求める
- それぞれの偏差を求める
- 偏差の積の平均値を求める
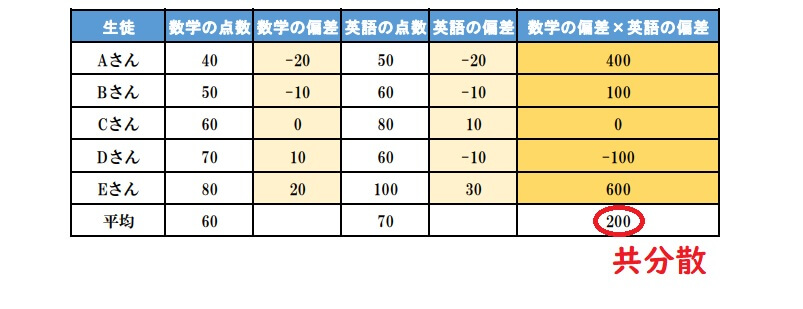

詳しい手順ともう1つに簡単な求め方について「共分散の求め方」で解説しています。


分散は1つのデータの散らばり度合いを示す数値でした。
それに対して、共分散は「2組の対応するデータ間の関係を表す数値」です。
相関係数
相関係数とは、「2つのデータ間にある関係の強さを表す指標」です。
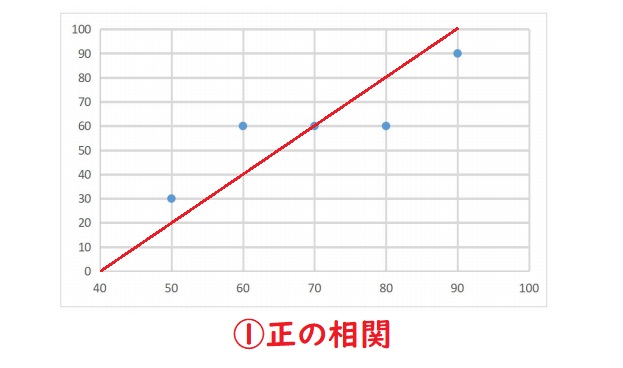

①のグラフようにx軸の値が大きくなるにつれて、y軸の値も大きくなっていく関係を正の相関があるといいます。
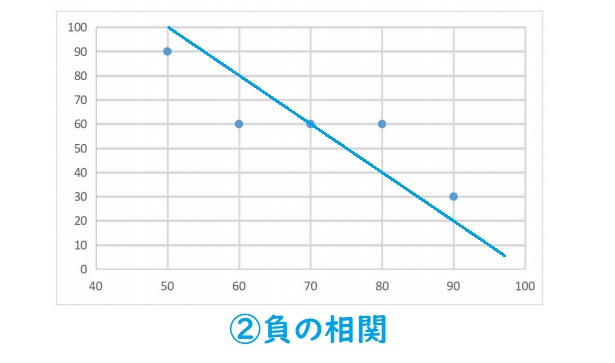

逆に②のグラフには右に行くにつれ下がっているので、負の相関があるといいます。
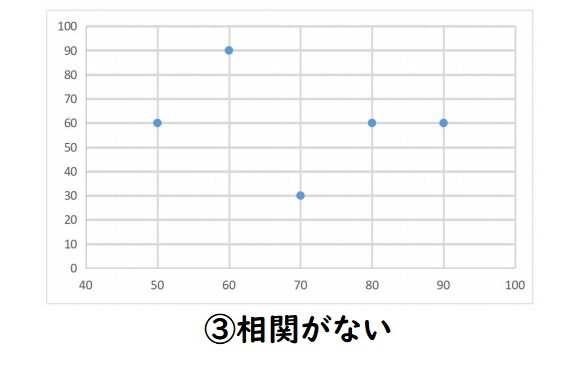

③のグラフのように2つのデータ間に関係がないと思われるものを相関がないまたは相関関係がないといいます。
相関係数の求め方
相関係数の求め方を解説していきます。
相関係数の公式
\(x,y\)それぞれの標準偏差を\(s_{x},s_{y}\)として、共分散を\(s_{xy}\)とする。
\[\displaystyle r=\frac{s_{xy}}{s_{x} s_{y}}\]
共分散の求め方①
- 平均値を求める
- 偏差を求める
- 共分散を求める
- 分散を求める
- 標準偏差を求める
- 相関係数を計算する
相関係数を求めるには、途中で「共分散」「分散」「標準偏差」を求める必要があります。
それらがまだ理解できていない方は、さきにそちらを解決させましょう。
例として相関係数を求める手順を1つ示します。
相関係数の例題
5人が数学と英語のテストを受けたとします。
x:数学の点数 y:英語の点数
それぞれの点数が、
(x,y)=(40,50)(50,60)(60,80)(70,60)(80,100)
このとき、数学と英語のテスト結果のあいだにある相関係数を求めましょう。
1.平均値を求める
数学、英語それぞれの平均点を求めます。
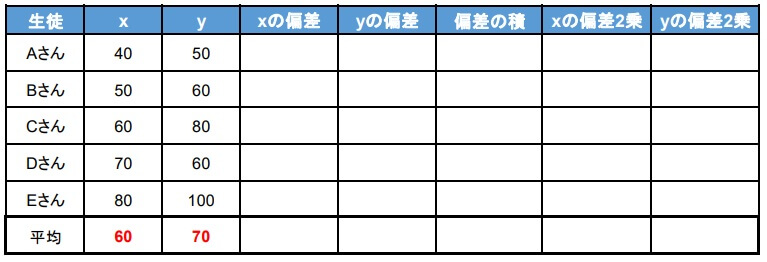

2.偏差を求める
次に偏差を求めます。
偏差とは「データ値と平均値との差」を指します。
⇒偏差値とは?偏差値の意味と求め方をズバリ解説します!
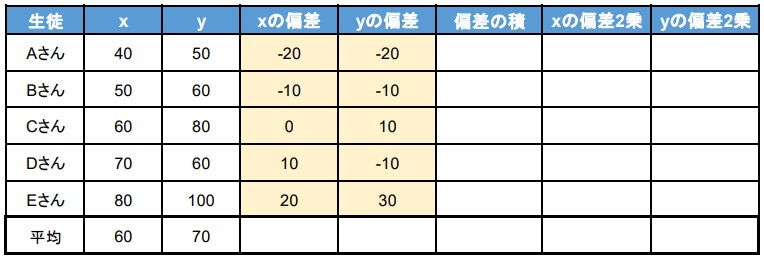

3.共分散を求める
2で求めたそれぞれの偏差を掛け合わせて、共分散を求めます。
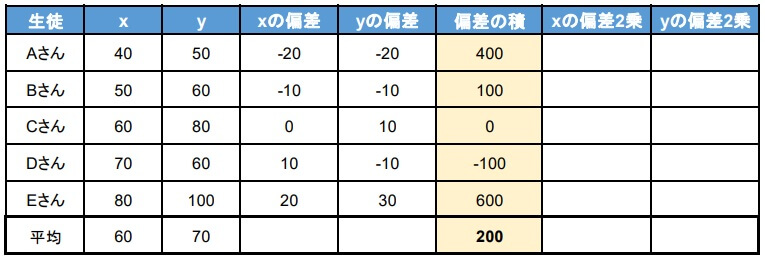

4.分散を求める
\(x,y\)それぞれの分散を求めます。
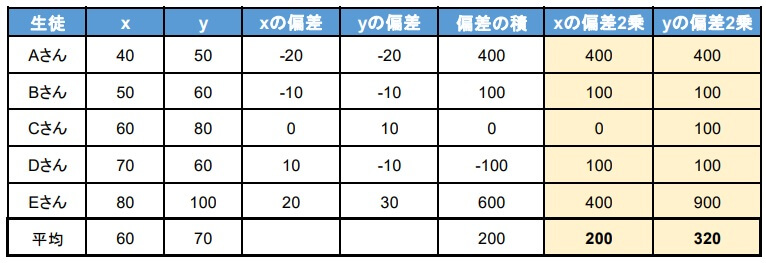

5.標準偏差を求める
4で求めた分散の正の平方根を計算して、標準偏差を求めます。
標準偏差は分散の正の平方根なので、
\(x\)の標準偏差:\(s_{x}=\sqrt{200}=10\sqrt{2}\)
\(y\)の標準偏差:\(s_{y}=\sqrt{320}=8\sqrt{5}\)
6.相関係数を計算する
長い道のりでしたが、最後に共分散、標準偏差を代入して相関係数を求めます。
\begin{eqnarray}
\displaystyle r&=&\frac{s_{xy}}{s_{x} s_{y}}\\
&=&\displaystyle \frac{200}{10\sqrt{2}×8\sqrt{5}}\\
&=&\displaystyle \frac{5}{2\sqrt{10}}\\
&≒&\displaystyle 0.79
\end{eqnarray}
したがって相関係数0.79を求めることができました。
「相関係数の意味と求め方」ではもう少し詳しく相関係数について解説しています。


データの分析 まとめ
今回はデータの分析について「完全攻略」記事としてまとめました。
データの分析に関する記事を網羅的にまとめましたが、詳しいポイントは各単元の記事で解説しています。
そちらもぜひ参考にしてください。
データの分析以外の単元についてもまとめ記事を出しています。
まとめ記事
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは今回も最後まで読んでくださってありがとうございました。
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。







コメント