四分位範囲と四分位偏差の意味と求め方

高校生

計算に困っていたので助かりました！

今回は四分位範囲と四分位偏差に関する悩みを解決していきます。

突然、四分位偏差を聞かれたら困りますよね。

しかもなかなか出題されないのでついつい忘れてしまいます。

シータ

四分位偏差はそこまで難しくないよ！

今回は「四分位範囲」「四分位偏差」の意味に加え、それぞれの求め方についても紹介します。

四分位範囲とは？

四分位範囲は、データの値を大きい順に並べたときの、中央の50%のデータの散らばりの度合いを表しています。

四分位範囲は、「第3四分位数-第1四分位数」ですが四分位範囲の求め方は次の項で解説します。

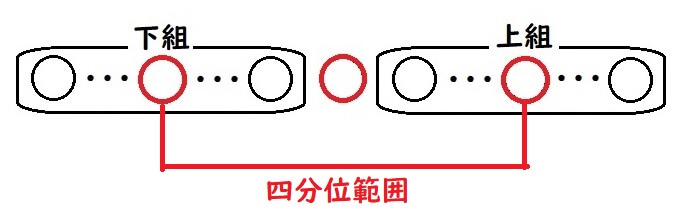
四分位範囲を使うメリットは「中央周辺の値しか考慮しないので、異常値の影響を受けにくい点」です。

データの値が中央値の周りに集中しているときは、四分位範囲は小さくなります。

四分位範囲は英語で「Interquartile range」と言うため、IQRと書くこともあります。

四分位範囲の求め方

四分位範囲の求め方を詳しく解説します。

まずは四分位数を求めます。

四分位数が求められたら、第3四分位数と第1四分位数の差を求めます。

四分位範囲=第3四分位数-第1四分位数

これで四分位範囲を求めることができます。

第１四分位数や第３四分位数がイマイチわからない方は「四分位数の求め方をわかりやすく解説！」を先にご覧ください。

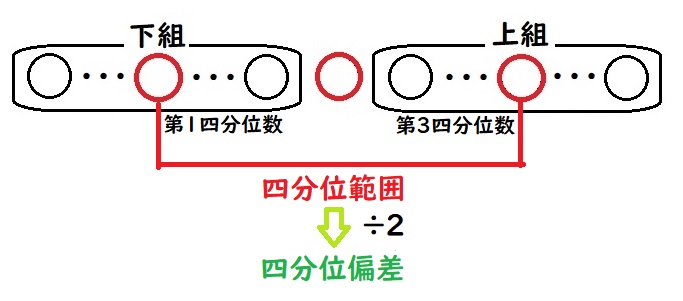
四分位偏差と求め方

四分位範囲の半分を四分位偏差といいます。

つまり、\(\displaystyle \frac{四分位範囲}{2}=\frac{第3四分位数-第1四分位数}{2}\)です。

「四分位範囲」「四分位偏差」　まとめ

今回はデータの分析から四分位範囲・四分位偏差についてまとめました。

他にも、教科書に内容に沿った解説記事を挙げています。

お気に入り登録して定期試験前に確認してください。

最後まで読んでくださりありがとうございました。

みんなの努力が報われますように！