入力した値の平均値を算出します。
値をカンマ(,)で区切って入力後に算出ボタンクリックしてください。
入力データ数:
合計:
平均値:
 高校生
高校生計算に困っていたので助かりました!
数学Ⅰデータの分析で欠かせないのが『平均値』です。
「平均値はどうやって求める?」
「中央値との違いはなに?」
今回はデータの中でも平均値に関するこんな悩みを解決します。
 高校生
高校生平均値の問題が多くて困ってます…
今回のテーマは『平均値』です。
1番基本的な平均値の求め方はこちらですね。
\begin{eqnarray}
\displaystyle 平均値=\frac{データの数値を全て足したもの}{データの個数}
\end{eqnarray}
定期テストの平均点は全員の合計点数を人数で割ることで求めます。
この記事では数学Ⅰ「データの分析」の理解を深めるために、度数分布表やヒストグラムから平均値を求める方法も解説していきます。
平均値の求め方
まずは平均値の求め方について3つのパターンに分けて解説します。
平均値の求め方
 シータ
シータ気になるものをクリックしてね
 高校生
高校生度数分布表からの求め方に困っています
基本の求め方
まずは最も基本的な平均値の求め方から確認しましょう。
全てのデータの値を足した和をデータの個数で割ることで平均値を求めることができます。
平均値の求め方
\begin{eqnarray}
\displaystyle 平均値=\frac{データの和}{データの個数}
\end{eqnarray}
つまり変数\(x\)の\(n\)個の値を\(x_1 ,x_2 ,x_3 ,…,x_n\)とするとき、
\[\displaystyle xの平均=\frac{x_1 +x_2 +x_3 +…+x_n}{n}\]
少し難しい式ですが、やっていることは
- すべてのデータの値を足す
- 1で求めた値をデータの個数で割る
たったこれだけで平均値を求められるので、やり方を覚えてしまえば難しい計算ではないと思います。
 高校生
高校生これならできそうです!
度数分布表から平均値を求める
次は度数分布表から平均値を求める方法を解説します。
ポイント
「度数分布表ってなんだっけ?」
こんな方はまずこちらの記事からご覧ください。
度数分布表から平均値を求めるには大きく4つのステップを踏みます。
簡単な流れ
- 階級値を求める
- 階級値×度数を求める
- 2⃣の総和を求める
- 3⃣を度数の合計で割る
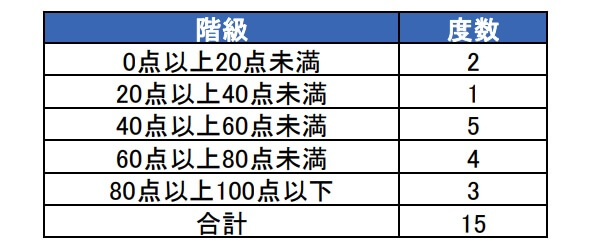
以下の度数分布表の平均値を求めていきます。
step
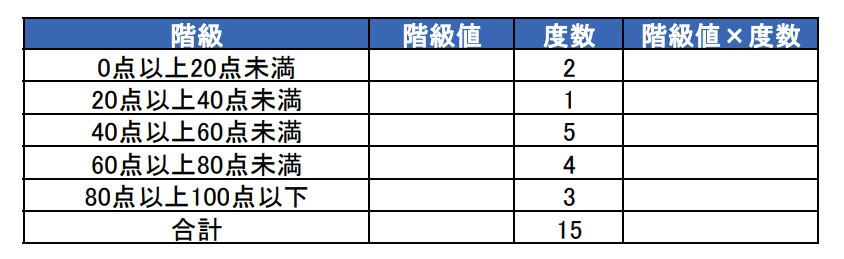
1階級値を求める
まずは各階級の階級値を求めます。
階級値は”階級の中央値”なので、\(\displaystyle \frac{階級の最大値+最小値}{2}\)で求めます。
step
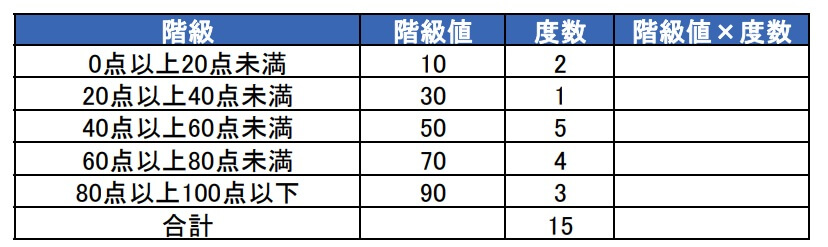
2階級値×度数を求める
1で求めた階級値と度数の積を求めます。
step
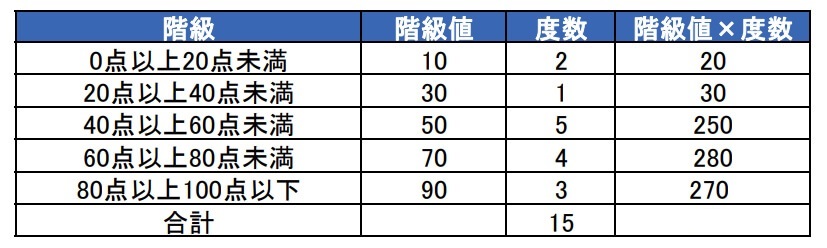
3Step2の総和を求める
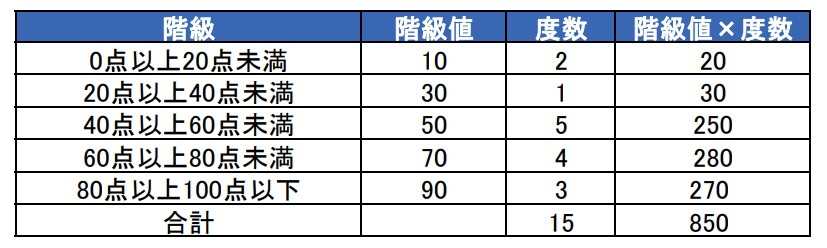
step
4Step3を度数の合計で割る
「階級値×度数」を度数の合計で割ったものが度数分布表の平均値です。
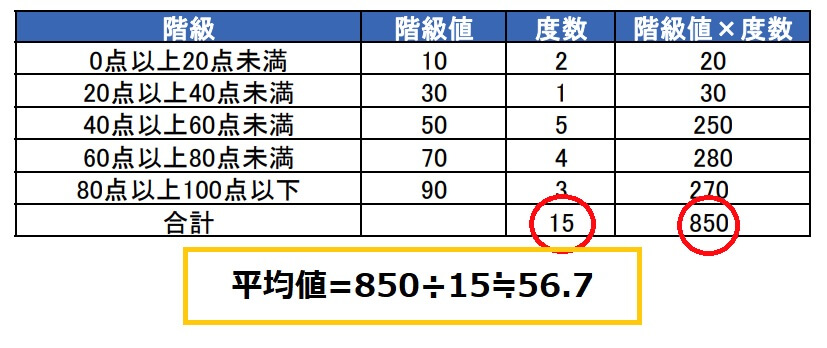
度数分布表については別の記事で解説しています。
度数分布表の平均値・中央値はこちら
ヒストグラムから平均値を求める
次はヒストグラムから平均値を求める方法を解説します。
ポイント
「ヒストグラムってなんだっけ?」
こんな方はまずこちらの記事からご覧ください。
ヒストグラムから平均値を求めるには大きく5つのステップを踏みます。
簡単な流れ
- ヒストグラムから度数分布表に直す
- 階級値を求める
- 階級値×度数を求める
- 2⃣の総和を求める
- 3⃣を度数の合計で割る
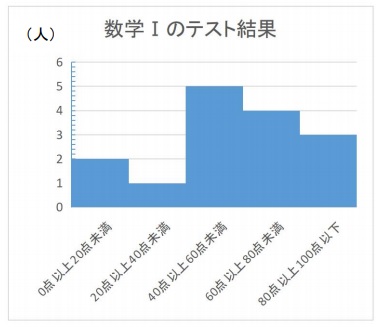
以下のヒストグラムから平均値を求めていきます。

step
1ヒストグラムから度数分布表に直す
まずはヒストグラムから度数分布表に直しましょう。
むしろ度数分布表に直すことさえできれば、度数分布表の平均値の求め方と全く同じです。


 高校生
高校生step
2階級値を求める

度数分布表が作れたら、各階級の階級値を求めます。
階級値は”階級の中央値”なので、\(\displaystyle \frac{階級の最大値+最小値}{2}\)で求めます。

step
3階級値×度数を求める
STEP2で求めた階級値と度数の積を求めます。
step
4Step3の総和を求める

step
5Step4を度数の合計で割る
「階級値×度数」を度数の合計で割ったものがこの度数分布表の平均値です。

これでヒストグラムから平均値を求めることができました。
 高校生
高校生度数分布表の平均値が求め方を知っていれば簡単ですね!
ヒストグラムについては別の記事で解説しています。
ヒストグラムの平均値・中央値はこちら
平均値とは?
そもそも平均値とは何を表しているのか解説します。
例えば、高校生5人が数学のテストを受けて点数が以下のような結果だったとします。
| 生徒 | A | B | C | D | E |
|---|---|---|---|---|---|
| 点数 | 54 | 69 | 45 | 62 | 60 |
平均値はすべてのデータの値を足した和をデータの個数で割ります。
\(\displaystyle (54+69+45+62+60) \div 5=\frac{290}{5}=58\)(点)
したがって、この場合の平均値は58点となります。
ここで出てきた平均値58点というのは、5人の点数が均等になるように分配したときに58点で揃うということを意味します。

平均値と中央値の違い
ここまで平均値の求め方について解説しましたが、「平均値」と似た言葉に「中央値」というものがあります。
データを大きさ順に並べたときに、中央に位置する値を「中央値」と呼びます。
以下のようなデータの中央値は60点です。

「平均値」というと真ん中のイメージを持つ人もいると思いますが、実際はそうではありません。
平均値は全データの平均なので、必ずしも中央の値であるとは限らないのです。
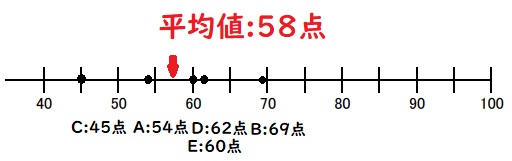
中央値について詳しくは別記事でまとめているので、気になる方はぜひご覧ください。
中央値の意味と求め方はこちら
平均値<練習問題>

今回確認した平均値を活用して例題に取り組んでみましょう。
高校生7人が英語のテストをしたところ以下のような結果になりました。
15人の平均値を求めなさい。
82 63 91 46 53
17 37(点)
平均値の求め方は、「すべてのデータの値を足して、データの個数で割る」でした。
\begin{eqnarray}
& &(82+63+81+46+53+23+37) \div 7\\
&=&385 \div 7\\
&=&55
\end{eqnarray}
したがって、7人の平均点は58点だと分かる。
平均値以外の代表値
今回は「平均値」に焦点を当てて解説していますが、データを扱う上で欠かせないものが他にも2つあります。
それが「中央値」と「最頻値」です。
データの代表値
以下の3つを代表値と呼びます。
- 平均値
- 中央値
- 最頻値
平均値以外の代表値についても別の記事で解説しているので、ぜひご覧ください。
データを大きさの順に並べたときに、真ん中にくる値を中央値といいます。
データの数が偶数のときは、真ん中にくる2つの値を足して2で割ったものが中央値となります。
データの中でもっとも出現頻度が高い値を最頻値といいます。
 高校生
高校生代表値はどれも覚えておく必要がありますか?
 シータ
シータどれも大切だから意味と求め方を必ず理解しておこう!
平均値の求め方 まとめ
今回はデータの分析から「平均値」についてまとめました。
平均値のポイント
基本的な平均値の求め方
平均値の求め方
\begin{eqnarray}
\displaystyle 平均値=\frac{データの和}{データの個数}
\end{eqnarray}
度数分布表から平均値を求める
簡単な流れ
- 階級値を求める
- 階級値×度数を求める
- 2⃣の総和を求める
- 3⃣を度数の合計で割る
ヒストグラムから平均値を求める
簡単な流れ
- ヒストグラムを度数分布表に直す
- 階級値を求める
- 階級値×度数を求める
- 2⃣の総和を求める
- 3⃣を度数の合計で割る
解き方を覚えればすぐに得点アップに繋がるので、この機会にしっかり理解しておきましょう。
データの分析には重要な公式がたくさんあります。
分散や相関係数についても別記事でまとめているので合わせてご覧ください。
他にもデータの分析に関する悩みがある方は「データの分析まとめ記事」をご覧ください。










コメント