今回は偏差値に関する疑問を解決していきます。
- 偏差値って何を表してるの?
- 標準偏差の求め方は?
テスト結果表などに「偏差値」と記載されている数字を見たことがありますか?
偏差値とはいったい何なのだろう?
 シータ
シータ50が真ん中って聞いたことあるよ
今回は偏差値の意味に加え、偏差値の見方についても紹介します。
本記事でしっかりと理解しておきましょう!
では順を追ってまとめていきます。
・偏差とは?
・偏差値とは?
・偏差値の見方
・偏差値の平均
・偏差値を使うメリット
・平均点と偏差値
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
偏差とは?
まず、偏差値の前に「偏差」について知っておきましょう。
偏差とは「データ値と平均値との差」です。
例えば、平均点60点のテストでAさんが70点,Bさんが50点を取ったとします。

この時の偏差は「データ値-平均値」なので、
Aさん \(70-60=10\)
Bさん \(50-60=-10\)
それぞれの偏差は上のようになります。
以上が、偏差についての解説です。
偏差値とは?

では本題に入りまして、
偏差値とは、「データの値を平均50、標準偏差10のデータに変換したときに示す値のこと」です。
 シータ
シータ難しい表現になってしまいましたね
要するに、「平均値を偏差値50として、データ値の位置づけを数字で表したもの」と考えておけば大丈夫です。
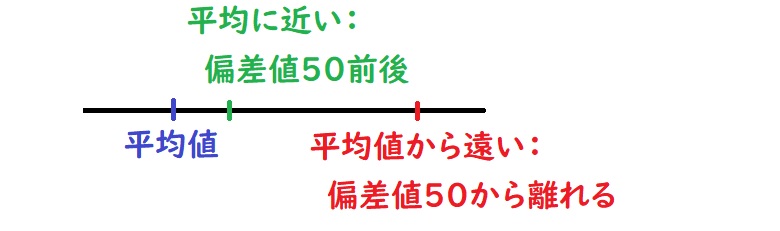
- データ値と平均値の差が大きいと、偏差値は50から離れる
- データ値と平均値との差が小さいと、偏差値は50に近づく
偏差値の見方
偏差値の見方を解説します。
偏差値からどれくらいの順位に位置するのかを読み取ることができます。
例えば1000人で数学Ⅰのテストを受けたとします。
偏差値70で上位2.275%に入り、22位前後に位置することが分かるのです。
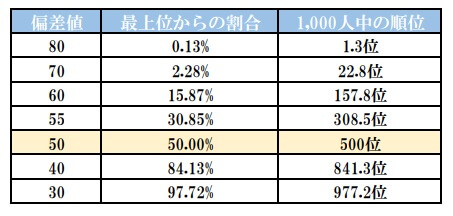
- 偏差値が高い⇒上位層
- 偏差値が少し高い⇒中間上位層
- 偏差値50⇒ちょうど真ん中
- 偏差値が少し低い⇒中間下位層
- 偏差値が低い⇒下位層
ざっくりですが上記のようなイメージで良いです。
偏差値を使うメリット

偏差値のメリットは、「データ値に左右されず、集団の中でどれくらいの位置にあるかが分かる点」です。
平均点が50点のテストで80点を取るのと、平均点が90点のテストで80点を取るのでは、同じ80点でも順位は大きく変わりますよね。
このように、データの値だけでは自分の位置づけがどこにあるかは分からないです。
テストで点数が低くても偏差値が高ければ上位層に属しているので、偏差値で点数を評価するようにしてください。
平均点と偏差値
データの値を公平に評価するには、平均との差だけではなく、集団全体のデータの散らばり具合も考慮する必要があります。
以下に数学Ⅰと数学Aのテスト結果を用意しました。

上の2つのテストはどちらも平均点が60点です。
この2つのテストでゆうや君が90点を取ったとします。
 高校生
高校生やった90点だ!!

数学Ⅰは30点から100点までデータの散らばりが大きいことが分かります。
一方で数学Aの場合は平均値周辺にデータが集まっていて、データの散らばりが小さいです。
データ全体が平均値周辺に集まっている場合、平均値の値から離れた点数は取りにくいので、平均値より高い点数を出すと偏差値は高くなります。
逆に、データ全体の散らばりが大きい時は、平均値から離れた値も出やすいので、平均値より高い得点でも偏差値はそこまで高くはなりません。
つまり、ゆうや君の成績は数学Aの方が偏差値が高くなります。
このように偏差値は「平均値との差」だけではなく、分散や標準偏差などの「データ全体の散らばりの度合い」を表す指標も考慮しています。
偏差値 まとめ
今回はデータの分析から偏差値についてまとめました。
平均値を偏差値50として、データ値の位置づけを数字で表したもの
偏差値の見方
- 偏差値が高い⇒上位層
- 偏差値が少し高い⇒中間上位層
- 偏差値50⇒ちょうど真ん中
- 偏差値が少し低い⇒中間下位層
- 偏差値が低い⇒下位層
偏差値のメリット
データ値に左右されず、集団の中でどれくらいの位置にあるかが分かる点
他にも、教科書に内容に沿った解説記事を挙げています。
お気に入り登録して定期試験前に確認してください。
最後まで読んでくださりありがとうございました。
みんなの努力が報われますように!

