入力した値の相関係数を算出します。
値をカンマ(,)で区切って入力後に算出ボタンクリックしてください。
2変量データの相関関数 r は以下の公式で表される。
r = sxysx・sy
= 1nΣ(xi – μx)(yi – μy)
√1nΣ(xi – μx)2・√1nΣ(yi – μy)2
ここで、n : 入力データ数、xi,yi : 各データ値、μx,μy : x,yの平均値
入力データ数(n):
x,yの共分散(sxy):
Xの標準偏差(sx):
Yの標準偏差(sy):より、
相間係数(r):となり、
 高校生
高校生計算に困っていたので助かりました!
今回は相関係数に関するこんな悩みを解決します。
「相関係数って何を表してるの?」
「相関係数の求め方は?」
 高校生
高校生相関係数ってなんだか難しそうなイメージがあります…
データの問題では分散や共分散と合わせて、相関係数を求める問題も多いですね。
分散と共分散を求めることができれば、相関係数は簡単に求めることができます。
本記事では相関係数の意味と求め方を解説します。
相関係数の意味
そもそも相関係数とは何なのか。
相関係数が表すものについて理解しておきましょう。
相関係数とは、「2つのデータ間にある関係の強さを表す指標」です。
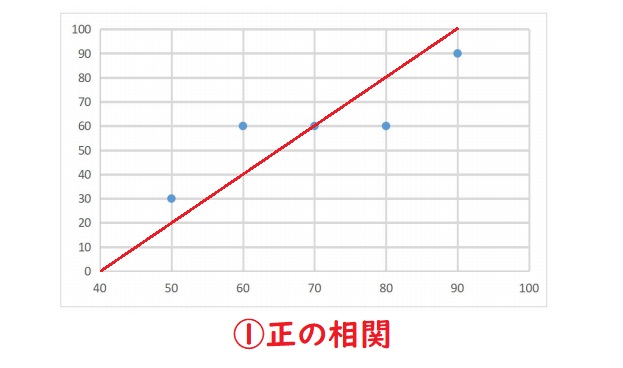
①のグラフようにx軸の値が大きくなるにつれて、y軸の値も大きくなっていく関係を正の相関があるといいます。
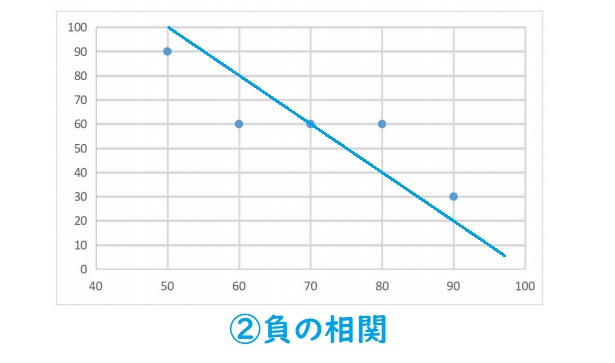
逆に②のグラフには右に行くにつれ下がっているので、負の相関があるといいます。
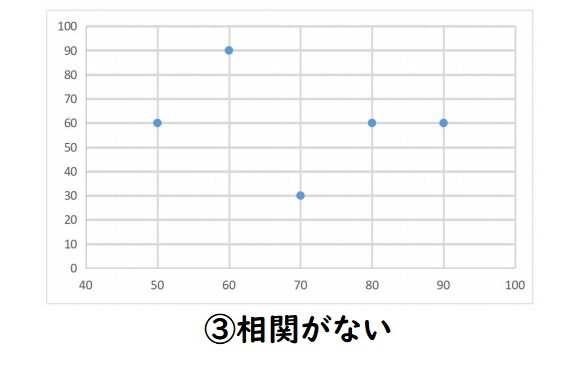
③のグラフのように2つのデータ間に関係がないと思われるものを相関がないまたは相関関係がないといいます。
相関係数の求め方<準備>
相関係数の求め方を解説する前に準備として、必要な公式を復習します。
相関係数を求めるにあたって、2つのデータの共分散とそれぞれの分散、標準偏差を求める必要があります。
共分散\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\(n\)はデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
標準偏差\(x\)の標準偏差\(s_x\)は次の公式で求める
\(n\)はデータの総数
\(x_i\)は個々の数値
\(\overline{x}\)はxの平均値
別の記事で詳しく解説しています
⇒共分散の意味と簡単な求め方を5分で解説!!
⇒標準偏差とは?標準偏差の意味と求め方を徹底解説します
[st-mybutton class=”” url=”https://math-travel.jp/data/” title=”データの分析まとめ記事” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]
相関係数の求め方
相関係数の求め方を解説していきます。
\(x,y\)それぞれの標準偏差を\(s_{x},s_{y}\)として、共分散を\(s_{xy}\)とする。
相関係数の求め方
- 平均値を求める
- 偏差を求める
- 共分散を求める
- 分散を求める
- 標準偏差を求める
- 相関係数を計算する
x:数学の点数 y:英語の点数
それぞれの点数は
(x,y)=(40,50)(50,60)(60,80)(70,60)(80,100)
この時の相関係数を求めます。
1.平均値を求める
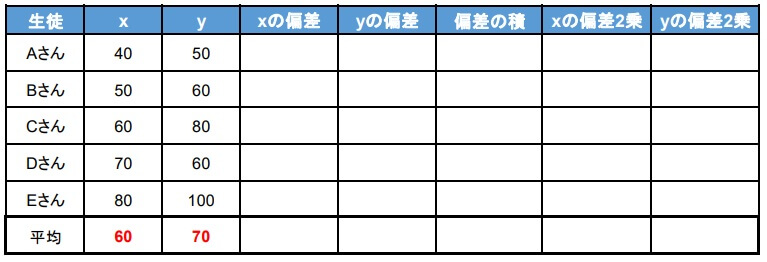
数学、英語それぞれの平均点を求めます。
2.偏差を求める
つぎに偏差を求めます。
偏差とは「データ値と平均値との差」を指します。
⇒偏差値とは?偏差値の意味と求め方をズバリ解説します!
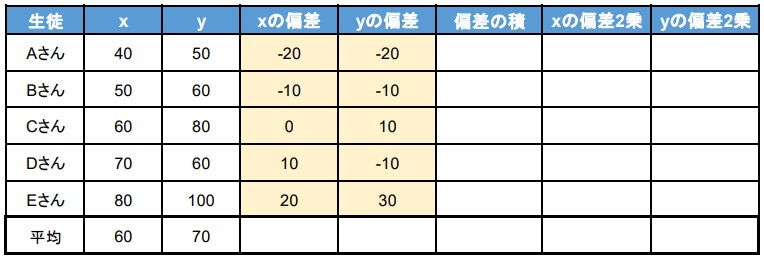
3.共分散を求める
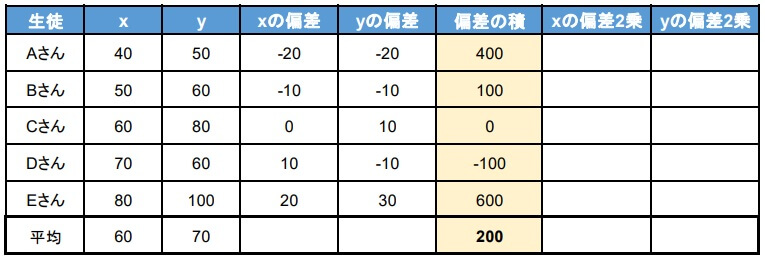
2で求めたそれぞれの偏差を掛け合わせて、共分散を求めます。
4.分散を求める
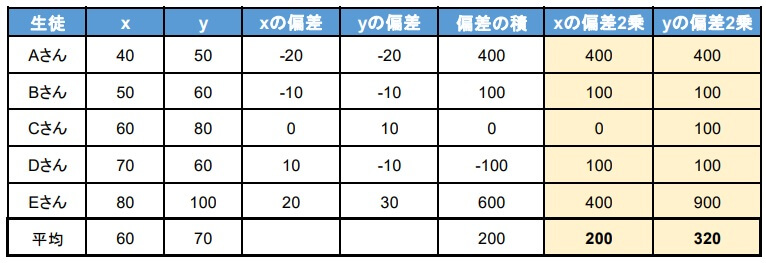
\(x,y\)それぞれの分散を求めます。
5.標準偏差を求める
4で求めた分散の正の平方根を計算して、標準偏差を求めます。
標準偏差は分散の正の平方根なので、
\(x\)の標準偏差:\(s_{x}=\sqrt{200}=10\sqrt{2}\)
\(y\)の標準偏差:\(s_{y}=\sqrt{320}=8\sqrt{5}\)
6.相関係数を計算する
長い道のりでしたが、最後に相関係数の公式に共分散、標準偏差を代入して相関係数を求めます。
\(\displaystyle r=\frac{s_{xy}}{s_{x} s_{y}}\)
\(\displaystyle =\frac{200}{10\sqrt{2}×8\sqrt{5}}\)
\(\displaystyle =\frac{5}{2\sqrt{10}}\)
\(\displaystyle ≒0.79\)
したがって相関係数を求めることができました。
 シータ
シータ分散や共分散の求め方を知らないと相関係数は求められないよ
相関係数のメリット
相関係数のメリットは、「2つのデータ間にある相関の強弱が分かりやすいこと」です。
相関係数と同じく2つのデータ間にある関係を表す指標に共分散があります。
共分散の注意点として、「扱っているデータの値が大きいと共分散の値も大きくなる点」がありました。
つまり、2つのデータ間にある相関関係がどれだけ強いのかが分かりにくいのです。
相関係数の場合は\(-1.00≦r≦1.00\)で表現されるので、2つのデータ間にある相関の強弱が分かりやすいのです。
相関係数<練習問題>

相関係数の意味を理解したところで、練習してみましょう。
相関係数の求め方
- 平均値を求める
- 偏差を求める
- 共分散を求める
- 分散を求める
- 標準偏差を求める
- 相関係数を計算する
x:数学の点数 y:英語の点数
それぞれの点数は
(x,y)=(50,30)(60,60)(70,60)(80,60)(90,90)
この時の相関係数を求めます。
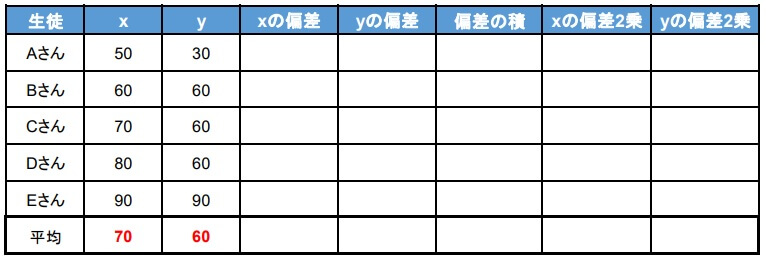
1.平均値を求める
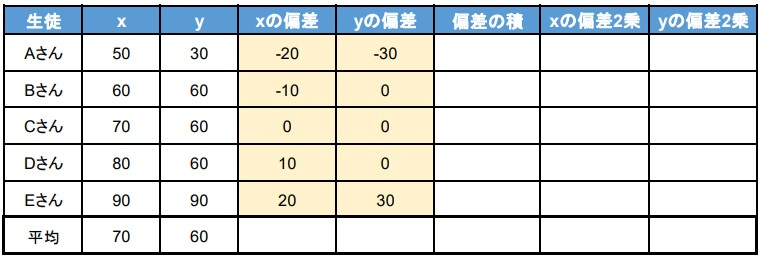
2.偏差を求める
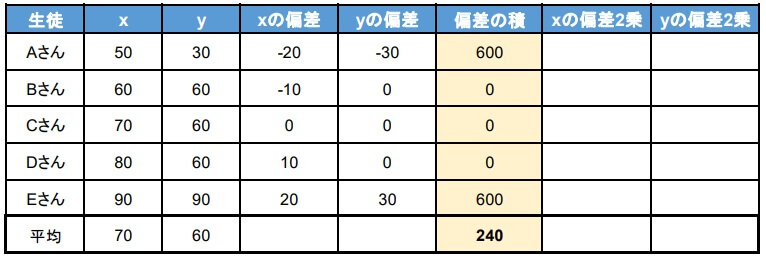
3.共分散を求める
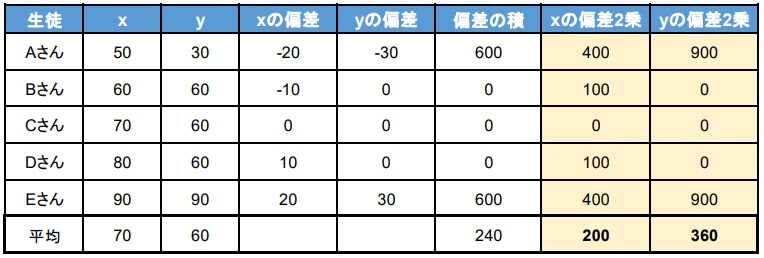
4.分散を求める
5.標準偏差を求める
\(x\)の標準偏差:\(s_{x}=\sqrt{200}=10\sqrt{2}\)
\(y\)の標準偏差:\(s_{y}=\sqrt{360}=6\sqrt{10}\)
6.相関係数を計算する
相関係数の公式に共分散、標準偏差を代入して相関係数を求めます。
\(\displaystyle r=\frac{s_{xy}}{s_{x} s_{y}}\)
\(\displaystyle =\frac{240}{10\sqrt{2} ×6\sqrt{10}}\)
\(\displaystyle =\frac{2}{\sqrt{5}}\)
\(\displaystyle ≒0.89\)
したがって求める相関係数は0.89である。
相関係数 まとめ
今回はデータの分析から相関係数についてまとめました。
2つのデータ間にある関係の強さを表す指標
相関係数の求め方
- 平均値を求める
- 偏差を求める
- 共分散を求める
- 分散を求める
- 標準偏差を求める
- 相関係数を計算する
相関係数のメリット
2つのデータ間にある相関の強弱が分かりやすいこと
他にも、教科書に内容に沿った解説記事を挙げています。
お気に入り登録して定期試験前に確認してください。
最後まで読んでくださりありがとうございました。
みんなの努力が報われますように!










コメント