データの範囲とは？範囲の求め方とデータの分析

数学Ⅰ「データの分析」に登場する用語の1つに『データの範囲』というものがあります。

データの範囲は、データの散らばりを考えるうえで欠かせない要素の一つです。

データの範囲（レンジ）は、データ分野の中では簡単な用語なので、今回で確実に覚えていきましょう！

範囲が分かるとデータの分布がイメージしやすくなります。

データの範囲とは？

冒頭の繰り返しになりますが、データの範囲というのは、「データの最大値と最小値の差」です。

つまり以下のようなデータが存在するとき、データの範囲は「25」となります。

調査したい数値がどれくらいの範囲に分布しているかを考えるときに活用します。

データの範囲の求め方

データの範囲の求め方はとても簡単です。

データを大きさ順に並び替えて、最大値と最小値の差を求めるだけです。

データの範囲を求めるメリット

データの範囲が分かることで、データ全体の散らばりの大きさがイメージできます。

つまり、集めたデータが似た数値ばかりなのか、それとも幅広い数値のデータが出ているのかを掴むことができます。

たとえば数学Ⅰのテスト結果を分析しましょう。

・Aクラスのテスト結果が以下のとき、範囲は10となります。

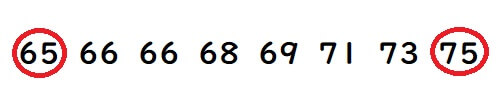
・Bクラスのテスト結果が以下のとき、範囲は40となります。

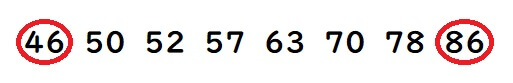
この2つを見比べてみると、Aクラスのテスト結果が70点周辺に集まっていることが分かります。

データの範囲が小さければ小さいほどデータが1点に集まっており、このことを「散らばりの度合いが小さい」と表現します。

一方でBクラスのようにデータの範囲が大きいことを、「散らばりの度合いが大きい」といいます。

データの範囲が分かることで、データ全体の散らばりの度合いを掴むことができます。

データの範囲の求め方【まとめ】

今回はデータの分析から範囲についてまとめました。

あまり難しい単元ではないので、確実に得点につなげましょう。

他にもデータの分析に関する悩みがある方は「データの分析まとめ記事」をご覧ください。