「和積の公式ってなんだっけ」
「公式が覚えられない」
今回は和積の公式＆積和の公式についてまとめました。
高校生和積＆積和の公式が覚えられません…
三角関数の中で1番くらいに覚えづらい公式が「和積の公式」「積和の公式」です。
和⇒積に変換するのが和積の公式です
和積の公式
一方で、積⇒和に変換するのが積和の公式です。
積和の公式
和積の公式も積和の公式も非常に覚えづらいですね。
本記事では和積の公式と積和の公式について解説しました。
それぞれの公式の導き方と覚え方についてまとめたので、ぜひ最後までご覧ください。
記事の内容
※本ページは学習アプリのプロモーションが含まれています。
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
積和の公式
まずは積和の公式を見てみましょう。
積和の公式
複雑な形をしていて、この公式を覚えるのは大変ですよね。
なぜ積和の公式がこんな形をしているのか、導き方を紹介します。
積和の公式《導き方》
積和の公式は加法定理を用いて導きます。
加法定理の公式や覚え方は「 加法定理の覚え方を5つ紹介！これでテストでも困らない！」で詳しく解説しています。加法定理が曖昧な人はこちらからチェックしておきましょう。
\(\sin\)の加法定理の式を用います。
①+②から
\[\sin(\alpha + \beta)+\sin(\alpha – \beta)=2 \sin \alpha \cos \beta\]
したがって、
\[\displaystyle \sin \alpha \cos \beta=\frac{1}{2}\{\sin(\alpha + \beta)+\sin(\alpha – \beta)\}\]
同様に①-②をすると、
\[\sin(\alpha + \beta)-\sin(\alpha – \beta)=2 \cos \alpha \sin \beta\]
したがって、
\[\displaystyle \cos \alpha \sin \beta=\frac{1}{2}\{\sin(\alpha + \beta)-\sin(\alpha – \beta)\}\]
次に\(\sin \alpha \sin \beta,\cos \alpha \cos \beta\)の導き方を紹介します。
\(\cos\)の加法定理を思い出して
③+④より
\[\cos(\alpha + \beta)+\cos(\alpha – \beta)=2\cos \alpha \cos \beta\]
したがって、
\[\displaystyle \cos \alpha \cos \beta=\frac{1}{2}\{\cos(\alpha + \beta)+\cos(\alpha – \beta)\}\]
同様に③-④より、
\[\cos(\alpha + \beta)-\cos(\alpha – \beta)=-2\sin \alpha \sin \beta\]
したがって、
\[\displaystyle \sin \alpha \sin \beta=-\frac{1}{2}\{\cos(\alpha + \beta)-\cos(\alpha – \beta)\}\]
このように積和の公式は加法定理を利用して導くことができます。
積和の公式
シータぼくは加法定理から導いて、積和の公式を使っているよ
和積の公式
次に和積の公式について解説します。
三角関数の和の形から積へ変形する公式です。
和積の公式
右辺の角度\(\displaystyle \frac{A+B}{2},\frac{A-B}{2}\)に注意しましょう。
和積の公式《導き方》
和積の公式は、積和の公式から変形して導きます。
積和の公式
\(\alpha+\beta=A,\alpha-\beta=B\)とすると、
\[\displaystyle \alpha=\frac{A+B}{2},\beta=\frac{A-B}{2}\cdots⑤\]
①,⑤より、
\[\displaystyle \sin \frac{A+B}{2} \cos \frac{A-B}{2}=\frac{1}{2}\{\sin A+\sin B\}\]
したがって、
\[\displaystyle \sin A+\sin B=2\sin \frac{A+B}{2} \cos \frac{A-B}{2}\]
同様に②,⑤から
\[\displaystyle \sin A-\sin B=2\cos \frac{A+B}{2} \sin \frac{A-B}{2}\]
③,⑤から
\[\displaystyle \cos A+\cos B=2\cos \frac{A+B}{2} \cos \frac{A-B}{2}\]
④,⑤から
\[\displaystyle \cos A-\cos B=-2\sin \frac{A+B}{2} \sin \frac{A-B}{2}\]
和積の公式を導くには、積和の公式が必要です。
そして積和の公式を導くために加法定理が必要なので、加法定理を必ず理解しておきましょう。
補足記事
加法定理の公式や覚え方は「 加法定理の覚え方を5つ紹介！これでテストでも困らない！」で詳しく解説しています。加法定理が曖昧な人はこちらからチェックしておきましょう。
和積＆積和の公式 覚え方
ここでは積和の公式の覚え方を考えましょう。
積和の公式
積和の公式を覚えてしまえば、和積の公式も導くことができます。
積和の公式は右辺が以下のような形をしています。
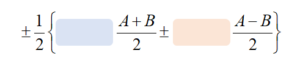
つまり、各式の符号と\(\sin,\cos\)だけを覚えれば大丈夫です。
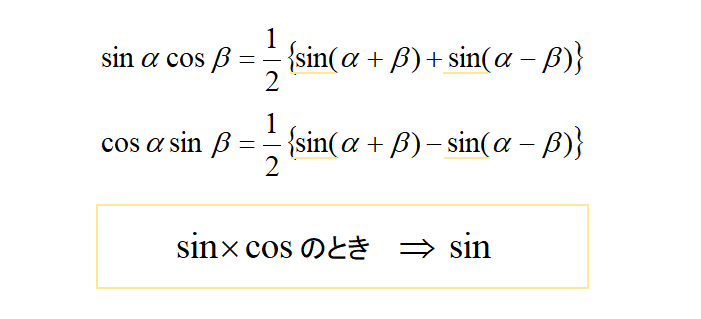
左辺の三角関数が異なるときは、右辺が\(\sin\)の和と差になりました。
一方で、左辺の三角関数が同じとき、右辺が\(\cos\)になります。
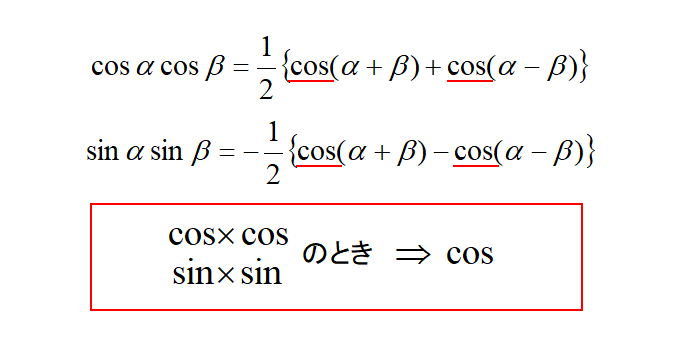
\(\sin \times \sin\)のときは、\(\displaystyle -\frac{1}{2}\)になるので注意しましょう。
ここまで積和の公式の覚え方を紹介しましたが、これでも覚えるのは大変です。
積和の公式がどうしても覚えられない人は、積和の公式を加法定理から導けるようにさえすれば問題ないです。
和積＆積和の公式 練習問題
和積の公式＆積和の公式を使った練習問題に挑戦しましょう。
まずは和積の公式に関する問題からです。
和積の公式 問題
和の式から積の形へ変形してみよう。
\[\sin 5 \theta +\sin \theta\]
これは和積の公式を用います。
\[\displaystyle \sin A+\sin B=2 \sin \frac{A+B}{2} \cos \frac{A-B}{2}\]
\(A=5 \theta,B=\theta\)として、
\begin{eqnarray}
\displaystyle \sin 5 \theta +\sin \theta&=&2 \sin \frac{5 \theta+\theta}{2} \cos \frac{5 \theta-\theta}{2}\\
&=&2 \sin 3 \theta \cos 2 \theta
\end{eqnarray}
次に積和の公式に関する問題です。
積和の公式 問題
積の式から和の形へ変形してみよう。
\[\sin 3 \theta \cos \theta\]
これは積和の公式を用います。
\[\displaystyle \sin \alpha \cos \beta=\frac{1}{2}\{\sin (\alpha+\beta)+\sin (\alpha-\beta)\}\]
\(\alpha=3 \theta,\beta=\theta\)として、
\begin{eqnarray}
\displaystyle \sin 3 \theta \cos \theta&=&\frac{1}{2}\{\sin (3 \theta+\theta)+\sin (3 \theta-\theta)\}\\
&=&\frac{1}{2}\left(\sin 4 \theta +\sin 2 \theta \right)
\end{eqnarray}
高校生なんとか解くことができました！
シータ公式を使いこなせるように練習していこう！
和積＆積和の公式 まとめ
今回は和積の公式＆積和の公式についてまとめました。
和積の公式
一方で、積⇒和に変換するのが積和の公式です。
積和の公式
和積の公式も積和の公式も非常に覚えづらいですね。
今回は和積の公式と積和の公式についてまとめましたが、三角関数には重要な公式がたくさんあります。
三角関数は公式も多く、定期テストの問題も作りやすいので三角関数は要注意の単元です。
三角比や三角関数に関する記事をピックアップしたので、ぜひ参考にしてください。
関連記事まとめ
みんなの努力が報われますように！
コメント