加法定理の公式まとめ！加法定理の重要ポイントを徹底解説！

「加法定理ってなんだっけ？」
「加法定理の公式が知りたい」
今回は加法定理の公式に関する悩みを解決します。

三角関数のなかでも加法定理は重要な公式の1つです。

加法定理を使うことで、\(\sin 105^\circ\)や\(\cos 15^\circ\)などの三角比を求めることができます。

本記事では加法定理の公式について徹底解説しています。

大事なことが詰まっているので、加法定理が苦手な方はぜひ最後までご覧ください。

※本ページは学習アプリのプロモーションが含まれています。

加法定理の公式

加法定理の公式について解説していきましょう。

覚えにくい公式なので、後ほど加法定理の覚え方を紹介します。

\(\sin\)の加法定理

\(\sin\)の加法定理は以下の公式です。

\(\sin\)の加法定理を使ってみましょう。

\begin{eqnarray}
\sin 105^\circ &=& \sin(45^\circ + 60^\circ)\\
&=&\sin 45^\circ \cos 60^\circ+\cos 45^\circ \sin 60^\circ\\
\displaystyle &=&\frac{1}{2 \sqrt{2}}+\frac{\sqrt{3}}{2 \sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{2}+\sqrt{6}}{4}
\end{eqnarray}

\begin{eqnarray}
\displaystyle \sin \frac{\pi}{12}&=&\sin (\frac{\pi}{3}-\frac{\pi}{4})\\
\displaystyle &=&\sin \frac{\pi}{3} \cos \frac{\pi}{4}-\cos \frac{\pi}{3} \sin \frac{\pi}{4}\\
\displaystyle &=&\frac{\sqrt{3}}{2 \sqrt{2}}-\frac{1}{2 \sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{6}+\sqrt{2}}{4}
\end{eqnarray}

\(\cos\)の加法定理

\(\cos\)の加法定理は以下の公式です。

\(\cos\)の加法定理を使うことで、

\begin{eqnarray}
\cos 105^\circ &=& \cos(45^\circ + 60^\circ)\\
&=&\cos 45^\circ \cos 60^\circ-\sin 45^\circ \sin 60^\circ\\
\displaystyle &=&\frac{1}{2 \sqrt{2}}-\frac{\sqrt{3}}{2 \sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{2}-\sqrt{6}}{4}
\end{eqnarray}

\begin{eqnarray}
\displaystyle \cos \frac{\pi}{12}&=&\cos (\frac{\pi}{3}-\frac{\pi}{4})\\
\displaystyle &=&\cos \frac{\pi}{3} \cos \frac{\pi}{4}+\sin \frac{\pi}{3} \sin \frac{\pi}{4}\\
\displaystyle &=&\frac{1}{2 \sqrt{2}}+\frac{\sqrt{3}}{2 \sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{2}+\sqrt{6}}{4}
\end{eqnarray}

などを求めることができます。

\(\tan\)の加法定理

\(\tan\)の加法定理は以下の公式です。

\(\tan\)の加法定理も使ってみます。

\begin{eqnarray}
\tan 105^\circ &=& \tan(45^\circ + 60^\circ)\\
\displaystyle &=&\frac{\tan 45^\circ+\tan 60^\circ}{1-\tan 45^\circ \tan 60^\circ}\\
\displaystyle &=&\frac{1+\sqrt{3}}{1-1 \cdot \sqrt{3}}\\
\displaystyle &=&\frac{1+\sqrt{3}}{1-\sqrt{3}}
\end{eqnarray}

\begin{eqnarray}
\displaystyle \tan \frac{\pi}{12}&=&\tan (\frac{\pi}{3}-\frac{\pi}{4})\\
\displaystyle &=&\frac{\tan \frac{\pi}{3}-\tan \frac{\pi}{4}}{1+\tan \frac{\pi}{3} \tan \frac{\pi}{4}}\\
\displaystyle &=&\frac{\sqrt{3}-1}{1+\sqrt{3} \cdot 1}\\
\displaystyle &=&\frac{\sqrt{3}-1}{1+\sqrt{3}}
\end{eqnarray}

加法定理を使うために、角度の表し方をまとめました。

求めたい角度	度数法	弧度法
\(\displaystyle 15^\circ , \frac{\pi}{12}\)	\(45^\circ-30^\circ\)	\(\displaystyle \frac{\pi}{4}-\frac{\pi}{6}\)
\(\displaystyle 75^\circ , \frac{5}{12}\pi\)	\(45^\circ + 30^\circ\)	\(\displaystyle \frac{\pi}{4}+\frac{\pi}{6}\)
\(\displaystyle 105^\circ , \frac{7}{12}\pi\)	\(60^\circ + 45^\circ\)	\(\displaystyle \frac{\pi}{3}+\frac{\pi}{4}\)
\(\displaystyle 165^\circ , \frac{11}{12}\pi\)	\(120^\circ+45^\circ\)	\(\displaystyle \frac{2}{3}\pi+\frac{\pi}{4}\)

加法定理の覚え方

「加法定理の公式が覚えられない！！」

こんな方も多いと思うので、加法定理の覚え方を紹介します。

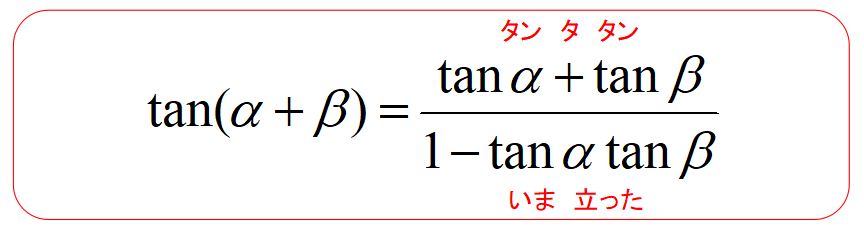
加法定理の覚え方はこちらの記事で詳しく解説しています。

加法定理の証明

加法定理を証明するには、まず\(\cos\)の加法定理を証明します。

今回は余弦定理を活用する証明を紹介します。

点\(P,Q\)の座標を\(P(\cos \alpha ,\sin \alpha),Q(\cos \beta ,\sin \beta)\)とします。

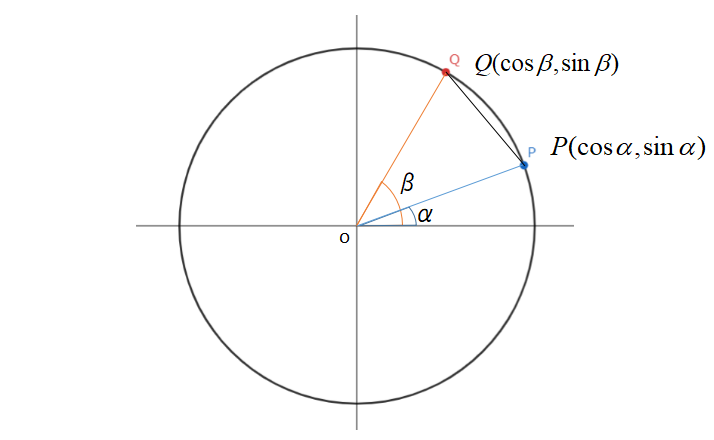
まずは余弦定理を用いて\(PQ^{2}\)を表します。

点\(P,Q\)は単位円上の点なので、\(OP=OQ=1\)が成り立ちます。

\begin{eqnarray}
PQ^{2}&=&OP^{2}+OQ^{2}-2OP \cdot OQ \cos (\beta – \alpha)\\
&=&1+1-2\cos(\beta – \alpha)\\
&=&2-2 \cos(\alpha – \beta) \cdots ①
\end{eqnarray}

次に点\(P\)と点\(Q\)の2点間の距離をもとめて、

\begin{eqnarray}
PQ^{2}&=&(\cos \beta -\cos \alpha)^{2}+(\sin \beta -\sin \alpha)^{2}\\
&=&2-2\cos \alpha \cos \beta – 2 \sin \alpha \sin \beta\\
&=&2-2(\cos \alpha \cos \beta +  \sin \alpha \sin \beta) \cdots ②
\end{eqnarray}

①,②より、

\[2-2 \cos(\alpha – \beta)=2-2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)\]

ゆえに、

\[2 \cos(\alpha – \beta)=2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)\]

したがって、

\[\cos(\alpha – \beta)=\cos \alpha \cos \beta +  \sin \alpha \sin \beta\]

余弦定理を使わない証明も知りたい方はこちらの記事をご覧ください。

⇒加法定理の証明を分かりやすく解説！2点の距離と余弦定理で示めす

その他の加法定理の証明

\(\cos (\alpha – \beta)\)の加法定理を示せれば、その他の加法定理は式変形で証明できます。

\begin{eqnarray}
\cos (\alpha+\beta)&=&\cos \{\alpha-(-\beta)\} \\
&=&\cos \alpha \cos (-\beta)+\sin \alpha \sin (-\beta)\\
&=&\cos \alpha \cos \beta-\sin \alpha \sin \beta\\
\end{eqnarray}

\begin{eqnarray}
\sin (\alpha+\beta)&=&\cos \{90-(\alpha+\beta)\}\\
&=&\cos \{(90-\alpha)-\beta\} \\
&=&\cos (90-\alpha) \cos \beta+\sin (90-\alpha) \sin \beta \\
&=&\sin \alpha \cos \beta+\cos \alpha \sin \beta
\end{eqnarray}

\begin{eqnarray}
\sin (\alpha-\beta)&=&\sin \{\alpha+(-\beta)\} \\
&=&\sin \alpha \cos (-\beta)+\cos \alpha \sin (-\beta) \\
&=&\sin \alpha \cos \beta-\cos \alpha \sin \beta
\end{eqnarray}

\begin{eqnarray}
\displaystyle \tan (\alpha+\beta)&=&\frac{\sin (\alpha+\beta)}{\cos (\alpha+\beta)} \\
\displaystyle &=&\frac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta }
\end{eqnarray}

分子, 分母を \(\cos \alpha \cos \beta\)で割って、

\begin{eqnarray}
\displaystyle 　&=&\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}
\end{eqnarray}
\begin{eqnarray}
\displaystyle \tan (\alpha-\beta)&=&\frac{\sin (\alpha-\beta)}{\cos (\alpha-\beta)} \\
\displaystyle &=&\frac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta+\sin \alpha \sin \beta}
\end{eqnarray}

分子, 分母を\(\cos \alpha \cos \beta \)で割って、

\begin{eqnarray}
\displaystyle &=&\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}
\end{eqnarray}

これですべての加法定理を証明することができました。

まずは\(\cos\)の加法定理を示すことを覚えておきましょう。

2倍角の公式

加法定理を活用した公式に“2倍角の公式”があります。

2倍角の公式は加法定理を活用して作ることができます。

\begin{eqnarray}
\sin 2 \alpha&=&\sin (\alpha + \alpha)\\
&=&\sin \alpha \cos \alpha + \cos \alpha \sin \alpha\\
&=&2\sin \alpha \cos \alpha
\end{eqnarray}

\begin{eqnarray}
\cos 2 \alpha&=&\cos (\alpha + \alpha)\\
&=&\cos \alpha \cos \alpha – \sin \alpha \sin \alpha\\
&=&\cos^{2} \alpha – \sin^{2} \alpha\\
&=&(1-\sin^{2} \alpha) – \sin^{2} \alpha\\
&=&1-2 \sin^{2} \alpha
\end{eqnarray}

2倍角の公式については別の記事で詳しくまとめました。

半角の公式

“半角の公式”は2倍角の公式を逆に活用した公式です。

\(\cos \alpha\)が分かっていれば、\(\displaystyle \frac{\alpha}{2}\)に関する三角比を求めることができるのです。

半角の公式についてはこちら

加法定理《練習問題》

加法定理を使った練習問題にチャレンジしてみましょう。

\begin{eqnarray}
\cos 75^\circ&=&\cos(30^\circ +45^\circ)\\
&=&\cos 30^\circ \cos 45^\circ- \sin 30^\circ \sin 45^\circ\\
\displaystyle &=&\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{2}} – \frac{1}{2} \times \frac{1}{\sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{6}- \sqrt{2}}{4}
\end{eqnarray}

\begin{eqnarray}
\displaystyle \sin \frac{7}{12}\pi&=&\sin(\frac{\pi}{3} + \frac{\pi}{4})\\
&=&\sin \frac{\pi}{3} \cos \frac{\pi}{4} + \cos \frac{\pi}{3} \sin \frac{\pi}{4}\\
\displaystyle &=&\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{2}} + \frac{1}{2} \times \frac{1}{\sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{6} + \sqrt{2}}{4}
\end{eqnarray}

\[\sin(\alpha + \beta)=\sin \alpha \cos \beta+ \cos \alpha \sin \beta \cdots ①\]

なので、

\(\cos \alpha,\sin \beta\)を求める必要があります。

\begin{eqnarray}
\cos^{2} \alpha&=&1-\sin^{2} \alpha\\
\displaystyle &=&1-\left(\frac{3}{5}\right)^{2}\\
&=&\frac{16}{25}
\end{eqnarray}

\(\displaystyle \frac{\pi}{2} < \alpha < \pi\)より、\(\cos \alpha<0\)

したがって、

\[\displaystyle \cos \alpha =\frac{4}{5} \cdots ②\]

\begin{eqnarray}
\sin^{2} \beta&=&1-\cos^{2} \beta\\
\displaystyle &=&1-\left(\frac{1}{2}\right)^{2}\\
&=&\frac{3}{4}
\end{eqnarray}

\(\displaystyle 0 < \beta < \frac{\pi}{2}\)より、\(\sin \beta<0\)

したがって、

\[\displaystyle \sin \beta=\frac{\sqrt{3}}{2} \cdots ③\]

①,②,③より、

\begin{eqnarray}
\sin(\alpha + \beta)&=&\sin \alpha \cos \beta+ \cos \alpha \sin \beta\\
\displaystyle &=&\frac{3}{5} \times \frac{1}{2}+\frac{4}{5} \times \frac{\sqrt{3}}{2}\\
\displaystyle &=&\frac{3+4\sqrt{3}}{10}
\end{eqnarray}

したがって、

\[\displaystyle\sin(\alpha + \beta)=\frac{3+4\sqrt{3}}{10}\]

加法定理の公式　まとめ

今回は加法定理の公式についてまとめました。

加法定理　まとめ

\(\sin 105^\circ\)や\(\displaystyle \cos \frac{\pi}{12}\)が突然出てくるとビックリしますが、加法定理を使えば問題ありません。

加法定理の公式は複雑な公式ですが、時間をかけてでも覚えましょう。

加法定理のほかにも三角関数には重要な公式がたくさんあります。

三角比や三角関数に関する記事をピックアップしたので、ぜひ参考にしてください。

みんなの努力が報われますように！

三角関数まとめ記事