3倍角の公式と覚え方！公式をマスターして得点アップ！

「3倍角の公式ってどんなの？」
「覚え方が知りたい」
今回は3倍角の公式に関する悩みを解決します。

三角関数の3倍角の公式を知っていますか？

3倍角の公式は以下のような形をしています。

とても複雑な公式なので、語呂合わせで覚えちゃいましょう。

本記事では３倍角の公式と覚え方について解説します。

後半に練習問題も用意したので、ぜひご活用ください。

※本ページは学習アプリのプロモーションが含まれています。

3倍角の公式

3倍角の公式はめったに使いませんが、こんな公式があることは知っておきましょう。

３倍角の公式というのは、角が３倍の形をしている三角関数の公式です。

\[\sin 3 \theta =3 \sin \theta-4 \sin ^{3} \theta\]

3倍角の公式の覚え方

3倍角の公式は複雑なので忘れてしまいますよね。

そこで3倍角の公式の覚え方を紹介します。

まずは\(\sin\)の3倍角の公式を語呂合わせで覚えましょう。

3倍角の公式は語呂合わせすら覚えづらいですね。

次に\(\cos\)の語呂合わせも紹介します。

\(\tan\)の語呂合わせは調べても見つからなかったので、気合で覚えましょう…（笑）

３倍角の公式　証明

３倍角の公式は加法定理を応用して証明します。

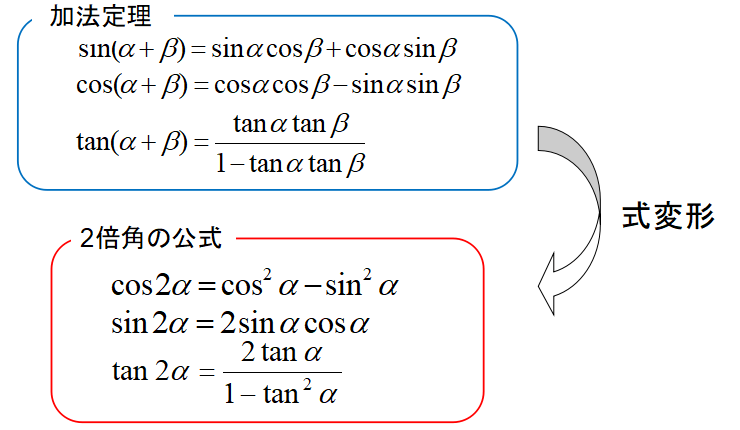
加法定理から確認したい方はこちらがおすすめ

それでは、それぞれの公式の証明をしていきます。

\(\sin\)の３倍角の公式

\(\sin\)の加法定理を使います。

\[\sin(α+β)=\sin α \cos β+\cos α \sin β\]

ここで\(α=2 \theta,β=\theta\)に置き換えると、

\begin{eqnarray}
\sin 3 \theta &=&\sin (2 \theta+\theta)\\
&=&\sin 2 \theta \cos \theta+\cos 2 \theta \sin \theta\\
&=&2 \sin \theta \cos \theta \cdot \cos \theta+(1-2 \sin ^{2} \theta) \sin \theta\\
&=&2 \sin \theta \cos ^{2} \theta+\sin \theta-2 \sin ^{3} \theta\\
&=&2 \sin \theta(1-\sin ^{2} \theta)+\sin \theta-2 \sin ^{3} \theta\\
&=&3 \sin \theta-4 \sin ^{3} \theta
\end{eqnarray}

したがって、

\[\sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta\]

\(\cos\)の３倍角の公式

\(\cos\)も同様の手順で証明します。

\(\cos\)の加法定理を使って、

\[\cos(α+β)=\cos α \cos β – \sin α \sin β\]

\(α=2\theta,β=\theta\)とすると、

\begin{eqnarray}
\cos 3 \theta &=&\cos (2 \theta+\theta)\\
&=&\cos 2 \theta \cos \theta-\sin 2 \theta \sin \theta\\
&=&(2 \cos ^{2} \theta-1) \cos \theta-2 \sin \theta \cos \theta \cdot \sin \theta\\
&=&2 \cos ^{3} \theta-\cos \theta-2 \sin ^{2} \theta \cos \theta\\
&=&2 \cos ^{3} \theta-\cos \theta-2(1-\cos ^{2} \theta) \cos \theta\\
&=&4 \cos ^{3} \theta-3 \cos \theta
\end{eqnarray}

したがって、

\[\cos 3 \theta =4 \cos^{3} \theta-3 \cos \theta\]

\(\tan\)の３倍角の公式

最後に\(\tan\)の3倍角の公式を証明します。

\(\tan\)の加法定理を用いて、

\[\displaystyle \tan(α+β)=\frac{\tan α + \tan β}{1-\tan α \tan β}\]

\(α=2\theta,β=\theta\)とすると

\begin{eqnarray}
\tan 3 \theta&=&\tan (2 \theta+\theta)\\
\displaystyle &=&\frac{\tan 2 \theta+\tan \theta}{1-\tan 2 \theta \tan \theta}\\
\displaystyle &=&\frac{\frac{2 \tan \theta}{1-\tan ^{2} \theta}+\tan \theta}{1-\frac{2 \tan \theta \cdot \tan \theta}{1-\tan ^{2} \theta}}
\end{eqnarray}

分母分子に \(1-\tan ^{2} \theta\) をかけると

\[\displaystyle \frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\]

となり、証明終了。

3倍角の公式の使い方

３倍角の公式は

\[\sin 3 \theta =3 \sin \theta-4 \sin ^{3} \theta\]

のような角が３倍の形をしているときに活躍します。

例題をもとに3倍角の公式の使い方を確認しましょう。

解答

\(\sin 3 \theta =3 \sin \theta-4 \sin ^{3} \theta\)を使いたいので、

\(\displaystyle \sin \theta=\frac{1}{3} \)を代入しましょう。

\begin{eqnarray}
\sin 3 \theta &=&3 \sin \theta-4 \sin ^{3} \theta\\
\displaystyle &=&3 \frac{1}{3}-4 \left(\frac{1}{3}\right)^{3}\\
\displaystyle &=&1-4 \frac{1}{27}\\
\displaystyle &=&\frac{23}{27}
\end{eqnarray}

したがって、

\[\sin 3 \theta=\frac{23}{27}\]

3倍角の公式《練習問題》

3倍角の公式を使って練習問題に挑戦しましょう。

解答

\(\sin,\cos,\tan\)それぞれの3倍角の公式を使うために、\(\cos \theta ,\tan \theta\)を求めましょう。

三角形の相互関係より、

\(\sin^{2} \theta +\cos^{2} \theta=1\)

なので、

\begin{eqnarray}
\cos^{2} \theta&=&1-\sin^{2} \theta\\
\displaystyle &=&1-(\frac{4}{5})^{2}\\
\displaystyle &=&\frac{9}{25}
\end{eqnarray}

\(\displaystyle 0<\theta<\frac{\pi}{2}\)より、

\[\displaystyle cos \theta=\frac{3}{5}\]

また、

\begin{eqnarray}
\displaystyle \tan \theta&=&\frac{\sin \theta}{\cos \theta}\\
\displaystyle &=&\frac{\frac{4}{5}}{\frac{3}{5}}\\
\displaystyle &=&\frac{4}{3}
\end{eqnarray}

したがって、

\(\displaystyle \sin \theta=\frac{4}{5}\),\(\displaystyle \cos \theta=\frac{3}{5}\),\(\displaystyle \tan \theta=\frac{4}{3}\)

ここからが本題です！

求めた値を3倍角の公式に代入します。

\begin{eqnarray}
\sin 3 \theta &=&3 \sin \theta-4 \sin ^{3} \theta\\
\displaystyle &=&3 \cdot \frac{4}{5}-4 \left(\frac{4}{5}\right)^{3}\\
\displaystyle &=&\frac{12}{5}-\frac{192}{125}\\
\displaystyle &=&\frac{108}{125}
\end{eqnarray}

\begin{eqnarray}
\cos 3 \theta&=&4 \cos ^{3} \theta-3 \cos \theta\\
\displaystyle &=&4 \left(\frac{3}{5}\right)^{3}-3 \cdot \frac{3}{5}\\
\displaystyle &=&\frac{108}{125}-\frac{9}{5}\\
\displaystyle &=&-\frac{107}{125}
\end{eqnarray}

最後に\(\tan 3 \theta\)を求めます。

\(\tan 3\theta\)は\(\displaystyle \tan 3 \theta =\frac{\sin 3 \theta}{\cos 3 \theta}\)から求めましょう。

※\(\tan\)の3倍角の公式も存在するよ！

\begin{eqnarray}
\displaystyle \tan 3 \theta &=&\frac{\sin 3 \theta}{\cos 3 \theta}\\
\displaystyle &=&\frac{\frac{108}{125}}{-\frac{107}{125}}\\
\displaystyle &=&-\frac{108}{107}
\end{eqnarray}

したがって、

\begin{eqnarray}
\displaystyle \sin 3 \theta&=&\frac{108}{125}\\
\displaystyle \cos 3 \theta&=&-\frac{107}{125}\\
\displaystyle \tan 3 \theta&=&-\frac{108}{107}
\end{eqnarray}

３倍角の公式　まとめ

今回は3倍角の公式についてまとめました。

3倍角の公式　まとめ

今回は3倍角の公式を中心に解説しました。

3倍角の公式は使う機会が少ないので忘れがちですよね。

3倍角の公式よりも加法定理や2倍角の公式の方が重要だと思うので、不安な方はこちらの記事もご覧ください。

また、三角関数の総復習ができる記事はこちらです。

三角関数のまとめ記事へ