θ＋π/2，θ+π三角関数の公式と導き方

三角関数の公式を理解して、やっと慣れてきた頃に

\(\sin (\theta+\pi)\)

こんなのとか

\(\displaystyle \cos (\theta+\frac{\pi}{2})\)

こんなのが出てくるんですよね…

ひとつひとつの公式を覚えていっても良いのですが結構大変です(^^;)

今回は三角関数の中でも、\(\displaystyle \theta + \frac{\pi}{2}\)や\(\theta + \pi\)の形をした三角関数の公式とその導き方を伝えていきます。

※本ページは学習アプリのプロモーションが含まれています。

シータ

気になる見出しをクリックして、
ぜひ最後までご覧ください。

θ＋π/2，θ+π三角関数の公式まとめ

まずはじめに公式を全部見せちゃいます。

公式が知りたかっただけの方は、ここまででOKです！

～\(-\theta\)の公式～
\(\sin (-\theta)=-\sin \theta\)
\(\cos (-\theta)=\cos \theta\)
\(\tan (-\theta)=-\tan \theta\)

～\(\displaystyle \theta+\frac{\pi}{2}\)の公式～
\(\displaystyle \sin (\theta+\frac{\pi}{2})=\cos \theta\)
\(\displaystyle \cos (\theta+\frac{\pi}{2})=-\sin \theta \)
\(\displaystyle \tan (\theta+\frac{\pi}{2})=-\frac{1}{\tan \theta}\)

～\( \theta+\pi \)の公式 ～
\(\sin (\theta+\pi)=-\sin \theta \)
\(\cos (\theta+\pi)=-\cos \theta \)
\(\tan (\theta+\pi)=\tan \theta\)

-θの三角関数

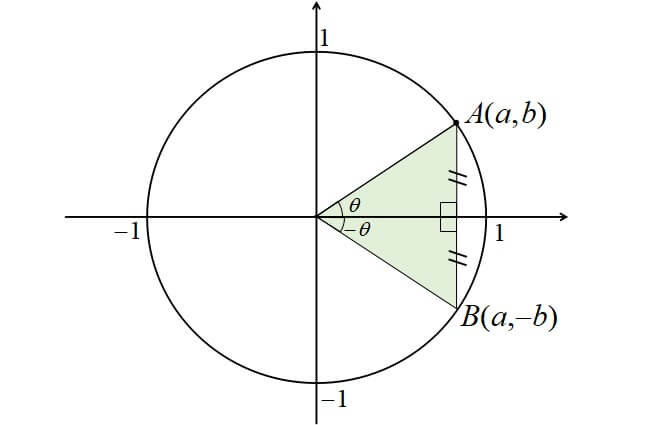
図を見てみると公式も納得できると思います。

今回はθを鋭角にしてみました。

-θというのは、単位円を逆回りにθだけ回せばよいので、

x座標は変わらずcos\(\theta\)、y座標の正負が逆になり-sin\(\theta\)になります。

\(\displaystyle tan \theta=\frac{sin \theta}{cos \theta}\)なので、

\(\displaystyle tan (-\theta)=\frac{sin (-\theta)}{cos (-\theta)}\)

\(\displaystyle tan (-\theta)=\frac{-sin \theta}{cos \theta}\)

\(tan (-\theta)=-tan (\theta)\)

θ＋π/2の三角関数

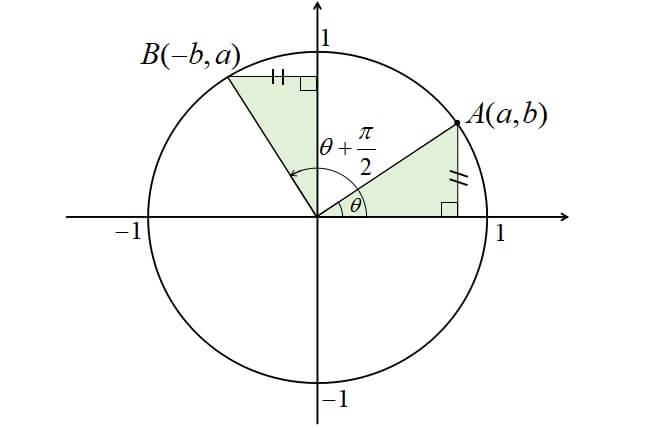
図のように\(\theta\)に対して、\(\displaystyle \frac{\pi}{2}\)回した先で合同な図形を描くことができます。

よってx座標の\(\displaystyle \cos (\theta+\frac{\pi}{2})\)は\(-\sin \theta \)

y座標の\(\displaystyle \sin (\theta+\frac{\pi}{2})\)は\(\cos \theta\)になります。

それに対して、\(\displaystyle \tan \theta=\frac{sin \theta}{cos \theta}\)なので、

\(\displaystyle \tan (\theta+\frac{\pi}{2})=\frac{sin (\theta+\frac{\pi}{2})}{cos (\theta+\frac{\pi}{2})}\)

\(\displaystyle \tan (\theta+\frac{\pi}{2})=\frac{\cos \theta}{-\sin \theta }\)

\(\displaystyle\tan (\theta+\frac{\pi}{2})=-\frac{1}{\tan \theta}\)

θ+πの三角関数

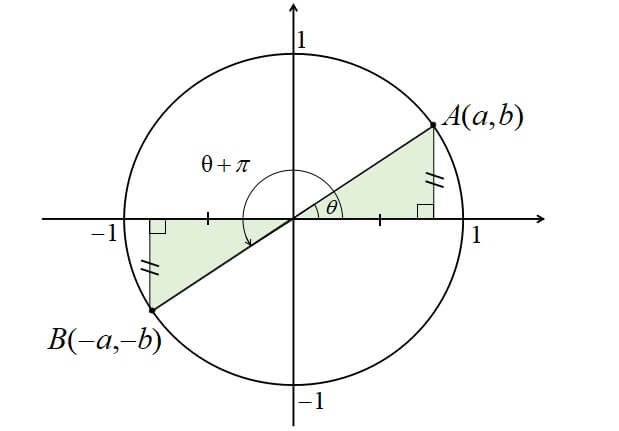
図のように\(\theta\)に対して、原点を中心に点対称な図形を描くことができる。

x座標もy座標も正負の符号を入れ替えることになり、

x座標は-cos\(\theta\)、y座標が-sin\(\theta\)になります。

それに対して、\(\displaystyle \tan \theta=\frac{sin \theta}{cos \theta}\)なので、

\(\displaystyle \tan (\theta+\pi)=\frac{sin (\theta+ \pi)}{cos (\theta+ \pi)}\)

\(\displaystyle \tan (\theta+\pi)=\frac{-sin \theta}{-cos \theta}\)

\(\tan (\theta+\pi)=\tan \theta\)

θ＋π/2，θ+πの導き方

ここまで公式を解説してきましたが、正直言うと覚えなくても良いです。

その代わり、公式の導き方を覚えておいてください。

導き方には２つあります。

θ＋π/2，θ+πの公式導き方①

加法定理を用いて計算で導く方法です。

\(\sin (\theta + \pi)=\sin \theta \cos \pi + \cos \theta \sin \pi\)

\(\sin (\theta + \pi)=\sin \theta \times (-1) + \cos \theta \times 0\)

\(\sin (\theta + \pi)=-\sin \theta\)

このように、加法定理に数字を代入することで求めることができます。

θ＋π/2，θ+πの公式導き方②

次は計算をしない覚え方を紹介です。

1つ目に関数の形です。

まず\(\pi\)の整数倍が絡むものは関数の部分が変化しません。
\(\displaystyle \frac{\pi}{2}\)の奇数倍が絡むものは sin⟺cos，\(tan⟺\displaystyle \frac{1}{\tan}\)と変化します。

２つ目に符号の部分です。

θが鋭角な単位円をイメージして、上の章で見せたように符号を確認します。

これで関数の部分と符号が分かったので変換ができました。

θ＋π/2，θ+π＜練習問題＞

今回学んだことを活かして、練習問題に挑戦してみましょう。

解答

１．\(\displaystyle \cos \frac{4}{5}\pi\)

\(\displaystyle =\cos (\frac{3}{10}\pi+\frac{\pi}{2})\)

\(\displaystyle=-\sin \frac{3}{10}\pi\)

２．\(\displaystyle \sin \frac{11}{9}\pi\)

\(\displaystyle =\sin (\frac{2}{9}\pi+\pi)\)

\(\displaystyle=-\sin \frac{2}{9}\pi\)

３．\(\displaystyle \tan \frac{13}{18}\pi\)

\(\displaystyle =\tan (\frac{2}{9}\pi+\frac{\pi}{2})\)

\(\displaystyle =-\frac{1}{\tan \frac{2}{9}\pi}\)

θ＋π/2，θ+π三角関数 おわりに

今回は三角関数からθ＋π/2，θ+πの三角関数の公式についてまとめました。

他にも、教科書に内容に沿ってどんどん解説記事を挙げていくので、

お気に入り登録しておいてもらえると定期試験前に確認できると思います。

では、ここまで読んでくださってありがとうございました。

みんなの努力が報われますように！