半角の公式の覚え方や使い方を徹底解説！

「半角の公式ってなんだっけ」
「半角の公式の使い方が知りたい」
今回は半角の公式に関するこんな悩みを解決します。

半角の公式は三角関数の重要な公式の1つです。

[st-mybox title=”半角の公式” fontawesome=”fa-exclamation-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}

[/st-mybox]

半角の公式を使うことで、\(\sin 15^\circ\)などを求めることができます。

ただ、半角の公式は見た目も複雑ですし、使い方が分かりづらい公式です。

きっと半角の公式や2倍角の公式がニガテな方も多いと思います。

本記事では半角の公式の使い方などを徹底解説しています。

三角関数が苦手な方にとって参考になることも多いので、ぜひ最後までご覧ください。

[st_af id=”13737″]

半角の公式

三角関数には重要な公式がいくつかあります。

[st-mybox title=”三角関数の重要公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• \(\sin,\cos,\tan\)の基本公式
• 正弦定理
• 余弦定理
• 加法定理
• 2倍角の公式　など

[/st-mybox]

そして半角の公式も三角関数の重要公式の1つです。

[st-mybox title=”半角の公式” fontawesome=”fa-exclamation-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}

[/st-mybox]

半角の公式はこんな式の形をしています。

その他の重要公式についてはこちらの記事でまとめました。

[st-card myclass=”” id=”2005″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

半角の公式　証明

半角の公式は\(\cos\)の2倍角の公式を変形して証明します。

[st-midasibox title=”2倍角の公式” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]

\begin{eqnarray}
\cos 2\theta&=&\cos^{2} \theta -\sin^{2} \theta\\
&=&1-2\sin^{2}\theta\\
&=&2\cos^{2} \theta-1
\end{eqnarray}

[/st-midasibox]

\(\cos\)の2倍角の公式

\[\cos 2\theta=1-2\sin^{2}\theta\]

\(\theta\)を\(\displaystyle \frac{\theta}{2}\)に置き換えると、

\[\displaystyle \cos 2\cdot \frac{\theta}{2}=1-2\sin^{2} \frac{\theta}{2}\]

ゆえに

\[\displaystyle \cos \theta=1-2\sin^{2} \frac{\theta}{2}\]

となり、式を整理すると

\[\displaystyle \sin^{2} \frac{\theta}{2}=\frac{1-\cos \theta}{2}\]

これで\(\sin\)の半角の公式を示すことができました。

\(\displaystyle \cos^{2} \frac{\theta}{2}\)も同様に、2倍角の公式から証明することができます。

\(\cos\)と\(\tan\)の証明はこちらの記事で紹介しています。

[st-card myclass=”” id=”2201″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

半角の公式　使い方

半角の公式は\(\theta\)を使って、\(\displaystyle \frac{\theta}{2}\)の三角比を求めます。

公式から分かるように、\(\cos \theta\)さえ分かれば半角の公式が使えます。

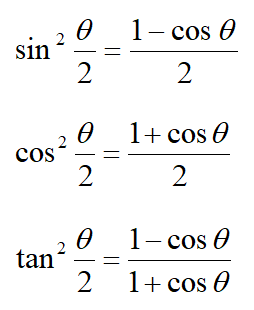
例として、\(\displaystyle \sin \frac{\pi}{12}\)を求めてみましょう。

\(\displaystyle \sin^{2} \frac{\pi}{12}\)を求めるには、\(\displaystyle \cos \frac{\pi}{6}\)は必要です。

\[\displaystyle \cos \frac{\pi}{6}=\frac{\sqrt{3}}{2} \cdots ①\]

①と半角の公式から、

\begin{eqnarray}
\displaystyle \sin^{2} \frac{\pi}{12}&=&\frac{1-\cos \frac{\pi}{6}}{2}\\
\displaystyle &=&\frac{1-\frac{\sqrt{3}}{2}}{2}\\
\displaystyle &=&\frac{2-\sqrt{3}}{4}
\end{eqnarray}

\(\displaystyle \sin \frac{\pi}{12}>0\)より、

\[\displaystyle \sin \frac{\pi}{12}=\frac{\sqrt{2-\sqrt{3}}}{2}\]

まずは\(\cos \theta\)を求めることを意識しましょう。

半角の公式を使う時の注意点

半角の公式を使う時の注意点が2つあります。

[st-mybox title=”注意ポイント” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• 2乗であること忘れない
• \(\theta\)の範囲に気を付けよう

[/st-mybox]

半角の公式で気を付けたい2点を解説します。

2乗であること忘れない

半角の公式は左辺が2乗であることに気を付けましょう。

半角の公式を忘れたときのために、2倍角の公式から半角の公式を作れるようにしておくと良いです。

\(theta\)の範囲に気を付けよう

もう1つ注意すべきなのが\(\theta\)の範囲です。

\(\displaystyle \sin^{2} \frac{\theta}{2}\)から\(\displaystyle \sin \frac{\theta}{2}\)を求めるとき、

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(\displaystyle \frac{\theta}{2}>0\)ならば、\(\displaystyle \sin \frac{\theta}{2}>0\)

\(\displaystyle \frac{\theta}{2}<0\)ならば、\(\displaystyle \sin \frac{\theta}{2}<0\)

[/st-mybox]

難しいことではありませんが、ここでミスするともったいないです。

\(\sin\)に限らず、\(\cos\)や\(\tan\)を求めるときにも範囲を意識するようにしましょう。

半角の公式の覚え方

半角の公式の覚え方を紹介します。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}
\end{eqnarray}

[/st-mybox]

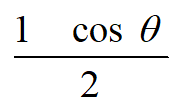
どちらもここまでは同じ形をしています。

ここで右辺の符号に注目しましょう。

[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

右辺には\(\cos \theta\)があります。

\(\displaystyle \sin^{2}\frac{\theta}{2}\)⇒\(\cos\)と異なるのでマイナス

\(\displaystyle \cos^{2}\frac{\theta}{2}\)⇒\(\cos\)と同じなのでプラス

[/st-mybox]

\(\tan\)の公式は丸暗記ではなく、

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\[\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}\]

[/st-mybox]

を利用して作りましょう。

\begin{eqnarray}
\displaystyle \tan^{2}\frac{\theta}{2}&=&\frac{\sin^{2} \frac{\theta}{2}}{\cos^{2} \frac{\theta}{2}}\\
\displaystyle &=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}

\(\sin\)と\(\cos\)の半角の公式さえ覚えておけば、\(\tan\)は簡単に求めることができます。

2倍角の公式

2倍角の公式も三角関数の重要な公式です。

[st-mybox title=”2倍角の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\begin{eqnarray}
\sin 2 \alpha&=&2 \sin \alpha \cos \alpha\\
\cos 2 \alpha&=&\cos^{2} \alpha – \sin^{2} \alpha\\
&=&1-2 \sin^{2} \alpha\\
&=&2 \cos^{2}-1\\
\displaystyle \tan 2\alpha&=&\frac{2 \tan \alpha}{1-\tan^{2}\alpha}
\end{eqnarray}

[/st-mybox]

その2倍角の公式は“加法定理”を活用して作ることができます。

[st-mybox title=”加法定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\begin{eqnarray}
\sin(\alpha+\beta)&=&\sin \alpha \cos \beta + \cos \alpha \sin \beta\\
\sin(\alpha-\beta)&=&\sin \alpha \cos \beta-\cos \alpha \sin \beta\\
\cos(\alpha+\beta)&=&\cos \alpha \cos \beta-\sin \alpha \sin \beta\\
\cos(\alpha-\beta)&=&\cos \alpha \cos \beta+\sin \alpha \sin \beta\\
\displaystyle \tan(\alpha+\beta)&=&\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\
\displaystyle \tan(\alpha-\beta)&=&\frac{\tan \alpha -\tan \beta}{1+\tan \alpha \tan \beta}
\end{eqnarray}

[/st-mybox]

加法定理の重要ポイントは別の記事でまとめました。

[st-card myclass=”” id=”6673″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

半角の公式《練習問題》

半角の公式を使った練習問題にチャレンジしてみましょう。

[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(0<\theta<\pi\)で\(\displaystyle \cos \theta=-\frac{2}{3}\)のとき、

\(\displaystyle \sin \frac{\theta}{2},\cos \frac{\theta}{2},\tan \frac{\theta}{2}\)を求めよう。

[/st-mybox]

\(\displaystyle \sin \frac{\theta}{2}\)を求める

\(\displaystyle \cos \theta=-\frac{2}{3}\)を半角の公式に代入して、

\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle &=&\frac{1+\frac{2}{3}}{2}\\
\displaystyle &=&\frac{5}{6}
\end{eqnarray}

ここで\(0<\frac{\theta}{2}<\frac{\pi}{2}\)なので、\(\sin \frac{\theta}{2}>0\)

したがって、

\[\displaystyle \sin \frac{\theta}{2}=\frac{\sqrt{30}}{6}\]

\(\displaystyle \cos \frac{\theta}{2}\)を求める

\(\sin\)と同様に、公式に代入して考えましょう。

\begin{eqnarray}
\displaystyle \cos^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle &=&\frac{1-\frac{2}{3}}{2}\\
\displaystyle &=&\frac{1}{6}
\end{eqnarray}

ここで\(0<\frac{\theta}{2}<\frac{\pi}{2}\)なので、\(\cos \frac{\theta}{2}>0\)

したがって、

\[\displaystyle \cos \frac{\theta}{2}=\frac{\sqrt{6}}{6}\]

\(\displaystyle \tan \frac{\theta}{2}\)を求める

\(\displaystyle \sin \frac{\theta}{2}=\frac{\sqrt{30}}{6},\cos \frac{\theta}{2}=\frac{\sqrt{6}}{6}\)

よって、

\begin{eqnarray}
\displaystyle \tan\frac{\theta}{2}&=&\frac{\sin \frac{\theta}{2}}{\cos \frac{\theta}{2}}\\
\displaystyle &=&\frac{\frac{\sqrt{30}}{6}}{\frac{\sqrt{6}}{6}}\\
&=&\sqrt{5}
\end{eqnarray}

したがって、

\[\displaystyle \tan \frac{\theta}{2}=\sqrt{5}\]

半角の公式　まとめ

今回は半角の公式についてまとめました。

[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]半角の公式　まとめ[/st-marumozi]

[st-mybox title=”半角の公式” fontawesome=”fa-exclamation-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}

[/st-mybox]

半角の公式は2倍角の公式を式変形することで証明できます。

[st-midasibox title=”2倍角の公式” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]

\begin{eqnarray}
\cos 2\theta&=&\cos^{2} \theta -\sin^{2} \theta\\
&=&1-2\sin^{2}\theta\\
&=&2\cos^{2} \theta-1
\end{eqnarray}

[/st-midasibox]

今回は半角の公式に焦点をあてて解説しました。

三角関数には加法定理や2倍角の公式など重要な公式がたくさんあります。

[st-card myclass=”” id=”2138″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

[st-card myclass=”” id=”2176″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

三角関数の重要ポイントをまとめた記事はこちら

[st-card myclass=”” id=”2005″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

三角比や三角関数に関する記事をピックアップしたので、ぜひ参考にしてください。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#b5d7b8″ bgcolor=”” borderwidth=”3″ borderradius=”5″ titleweight=”bold” fontsize=””]

• 加法定理の公式まとめ！加法定理の重要ポイントを徹底解説！
• 三角関数の公式(sin,cos,tan)と覚え方
• 半角の公式の覚え方や使い方を徹底解説！
• 和積＆積和の公式と覚え方
• 三角関数が分かる！重要公式の使い方を丁寧に解説！

[/st-mybox]

みんなの努力が報われますように！

[st-mybutton class=”margin50″ url=”https://math-travel.jp/sankakukansuu-matome/” title=”三角関数まとめ記事” rel=”” fontawesome=”” target=”_blank” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”2″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]