「2倍角の公式ってどんな公式？」
「どうやって使えばいいの？」
今回は2倍角の公式に関する悩みを解決します。
高校生公式をすぐに忘れちゃいます…
2倍角の公式は決して難しい公式ではありません。
見た目は難しそうにも見えますが、加法定理を応用した公式です。
難しい公式ではありませんが、三角関数における重要な公式です。
公式も覚えて欲しいし、いつでも使いこなせるように練習しておきましょう。
本記事では2倍角の公式について解説しました。
記事の後半に練習問題もあるので、2倍角に慣れていない方はぜひ最後までご覧ください。
記事の内容
※本ページは学習アプリのプロモーションが含まれています。
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
2倍角の公式
2倍角の公式は\(2 \alpha\)のように、角がある角の2倍のときに使う公式です。
2倍角の公式
\begin{eqnarray}
\sin 2 \alpha&=&2 \sin \alpha \cos \alpha\\
\cos 2 \alpha&=&\cos ^{2} \alpha-\sin ^{2} \alpha\\
&=&2 \cos ^{2} \alpha-1\\
&=&1-2 \sin ^{2} \alpha\\
\displaystyle \tan 2 \alpha&=&\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}
\end{eqnarray}
\(\sin\)や\(\cos\)のあとの角の部分が、2倍の形をしていたら2倍角の公式を使うことが多いです。
高校生2倍のときに使うから2倍角の公式なんですね！
2倍角の公式の求め方
2倍角の公式は加法定理を応用した公式です。
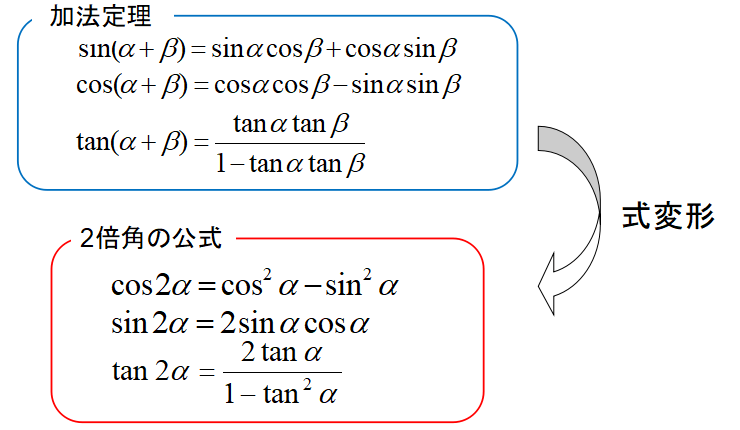
どのような式変形をして、2倍角の公式が成り立っているのかを解説します。
参考
加法定理から確認したい方はこちら
\(\sin\)の2倍角の公式
\(\sin\)も\(\cos\)も2倍角の公式を求める手順は同じです。
加法定理の公式を思い出して、\(\beta\)を\(\alpha\)に置き換えるだけです。
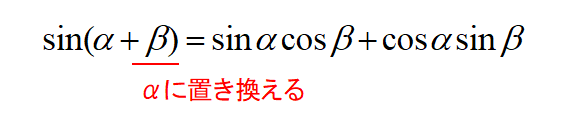
\(\sin\)の加法定理より、
\[\sin(\alpha + \beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta\]
ここで\(\beta\)を\(\alpha\)に置き換えると、
\begin{eqnarray}
\sin(\alpha + \alpha)&=&\sin \alpha \cos \alpha +\cos \alpha \sin \alpha\\
\sin 2\alpha&=&2\sin \alpha \cos \alpha
\end{eqnarray}
したがって、\(\sin\)の2倍角の公式
\[\sin 2\alpha=2\sin \alpha \cos \alpha\]
を求めることができました。
\(\cos\)の2倍角の公式
\(\cos\)も\(\sin\)と同様の手順で求めます。
\(\cos\)の加法定理より、
\[\cos(\alpha + \beta)=\cos \alpha \cos \beta – \sin \alpha \sin \beta\]
ここで\(\beta\)を\(\alpha\)に置き換えると、
\begin{eqnarray}
\cos(\alpha + \alpha)&=&\cos \alpha \cos \alpha – \sin \alpha \sin \alpha\\
\cos 2\alpha&=&\cos^{2} \alpha – \sin^{2} \alpha
\end{eqnarray}
\(\cos\)の2倍角の公式はまだ変形することができます。
三角関数の相互関係より、
\[\sin^{2} \theta + \cos^{2} \theta=1\]
\begin{eqnarray}
\cos 2\alpha&=&\cos^{2} \alpha – \sin^{2} \alpha\\
&=&\left(1-\sin^{2} \alpha \right) – \sin^{2} \alpha\\
&=&1-2 \sin ^{2} \alpha
\end{eqnarray}
同様に、
\begin{eqnarray}
\cos 2\alpha&=&\cos^{2} \alpha – \sin^{2} \alpha\\
&=&\cos^{2} \alpha – \left(1-\cos^{2} \alpha \right)\\
&=&2 \cos ^{2} \alpha-1
\end{eqnarray}
したがって、\(\cos\)の2倍角の公式
\begin{eqnarray}
\cos 2 \alpha&=&\cos ^{2} \alpha-\sin ^{2} \alpha\\
&=&2 \cos ^{2} \alpha-1\\
&=&1-2 \sin ^{2} \alpha
\end{eqnarray}
を求めることができました。
\(\tan\)の2倍角の公式
\(\tan\)の2倍角の公式も同様に求めます。
\(\tan\)の加法定理より、
\[\displaystyle \tan(\alpha +\beta)=\frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}\]
\(\beta\)を\(\alpha\)に置き換えて、
\[\displaystyle \tan (\alpha +\alpha)=\frac{\tan \alpha + \tan \alpha}{1-\tan \alpha \tan \alpha}\]
したがって、\(\tan\)の2倍角の公式
\[\displaystyle \tan 2 \alpha=\frac{2\tan \alpha}{1-\tan^{2} \alpha}\]
を求めることができました。
2倍角の公式 使い方
2倍角の公式を知っていても、使うことができなければ得点になりません。
例題を解きながら使い方を確認しましょう。
2倍角の公式 例題
\(\displaystyle \sin \theta=\frac{1}{3} \)のとき、\(\sin 2 \theta\)を求めよう。
ただし,\(\displaystyle 0<\theta<\frac{\pi}{2}\)とする。
解答
\(\sin 2 \theta\)を求めるので、2倍角の公式を使おうと考えます。
\[\sin 2 \theta=2 \sin \theta \cos \theta\]
\(\sin\)の2倍角の公式を使うには、\(\cos \theta\)を求める必要がありますね。
三角形の相互関係より
\[\sin^{2} \theta + \cos^{2} \theta=1\]
なので、
\[\displaystyle \left(\frac{1}{3} \right)^{2} + \cos^{2} \theta =1\]
\[\displaystyle \cos^{2} \theta =\frac{8}{9}\]
ここで,\(\displaystyle 0<\theta<\frac{\pi}{2}\)なので、
\[\displaystyle \cos \theta =\frac{2\sqrt2}{3}\]
\(\displaystyle \cos \theta =\frac{2\sqrt{2}}{3}\)を２倍角の公式に代入して、
\begin{eqnarray}
\sin 2 \theta&=&2 \sin \theta \cos \theta\\
\displaystyle &=&2 \cdot \frac{1}{3} \cdot \frac{2\sqrt{2}}{3} \\
\displaystyle &=&\frac{4\sqrt{2}}{9}
\end{eqnarray}
したがって、
\[\displaystyle \sin 2 \theta=\frac{4\sqrt2}{9}\]
計算式から分かるように、難しい計算は一切ありません。
2倍角の公式を覚えて、公式に代入するために必要な値を求めるだけです。
高校生難しいイメージがありましたが、できる気がしてきました！
シータ公式を覚えたあとは練習あるのみだよ！
《応用》半角の公式
2倍角を応用した公式に半角の公式というものがあります。
半角の公式
\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}
2倍角の公式が角を2倍した公式だったのに対して、半角の公式では角が半分になります。
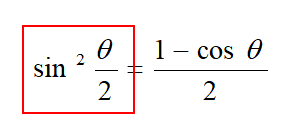
半角の公式は2倍角の公式を式変形しただけなので、すぐに使いこなせるようになると思います。
半角の公式は別の記事で詳しく解説しました。
2倍角の公式《練習問題》
2倍角の公式を用いて、練習問題に挑戦してみましょう。
練習問題1
\(\displaystyle 0<\theta<\frac{\pi}{2}, \sin \theta=\frac{4}{5}\)のとき,
\[\cos 2 \theta,\sin 2 \theta\]
を求めよう。
解答
\[\cos 2 \theta=1-2 \sin^{2} \theta \]
なので、
\begin{eqnarray}
\displaystyle \cos 2 \theta&=&1-2 \left(\frac{4}{5} \right)^{2}\\
\displaystyle &=&-\frac{7}{25}
\end{eqnarray}
三角形の相互関係より
\(\displaystyle \sin^{2} 2 \theta=1 – \cos^{2} 2 \theta\)
なので、
\begin{eqnarray}
\displaystyle \sin^{2} 2 \theta&=&1 – \cos^{2} 2 \theta\\
\displaystyle &=&1- \left(-\frac{7}{25} \right)^{2}\\
\displaystyle &=&1-\frac{49}{625}\\
\displaystyle &=&\frac{576}{625}
\end{eqnarray}
\(\displaystyle 0<\theta<\frac{\pi}{2}\)より,
\[\displaystyle \sin 2\theta=\frac{24}{25}\]
練習問題2
\(\displaystyle 0 < \theta < \frac{2}{3} \pi\)のとき,
関数\(y=\cos 2 \theta-2 \cos \theta\)の最大值と最小值を求めよ。
解答
まずは与えられた式を変形しましょう。
\begin{eqnarray}
y&=&\cos 2 \theta-2 \cos \theta\\
&=&\left(2 \cos ^{2} \theta-1 \right)-2 \cos \theta\\
&=&2\cos ^{2} \theta-2\cos \theta-1
\end{eqnarray}
右辺を平方完成をして、
\[\displaystyle 2\cos ^{2} \theta-2\cos \theta-1=2(\cos \theta-\frac{1}{2})^{2}-\frac{3}{2}\]
\(\displaystyle 0 < \theta < \frac{2}{3} \pi\)より,\(\displaystyle -\frac{1}{2} < \cos \theta < 1\)
したがって、
\(\displaystyle \cos \theta=-\frac{1}{2}\) のとき最大值 \(\displaystyle \frac{1}{2}\)
\(\displaystyle \cos \theta=\frac{1}{2}\) のとき最小值 \(\displaystyle -\frac{3}{2}\)
2倍角の公式 まとめ
今回は2倍角の公式についてまとめました。
2倍角の公式2倍角の公式
\begin{eqnarray}
\sin 2 \alpha&=&2 \sin \alpha \cos \alpha\\
\cos 2 \alpha&=&\cos ^{2} \alpha-\sin ^{2} \alpha\\
&=&2 \cos ^{2} \alpha-1\\
&=&1-2 \sin ^{2} \alpha\\
\displaystyle \tan 2 \alpha&=&\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}
\end{eqnarray}
\(\cos\)の2倍角の公式だけ、3パターンに変形できるので注意してください。
2倍角の公式は加法定理を応用して、公式を導くことができます。
加法定理の重要ポイントはこちらにまとめました。
三角関数の総復習がしたい方はこちらの記事がおすすめ
コメント