弧度法とは？弧度法の変換や面積公式すべて解説！

高校生

どういうのが弧度法ですか？

数Ⅱの三角関数では円の中心角を\(180^\circ\)や\(360^\circ\)といった度数法ではなく、\(\pi\),\(2\pi\)など弧度法で表します。

慣れるまでは難しく思えるかもしれません。

ぼくも始めはよく分からず使っていたので大丈夫です。

三角関数では弧度法を用いることが主流なので意味はしっかり押さえておきましょう。

本記事では弧度法の意味および度数法から弧度法への変換方法について解説していきます。

※本ページは学習アプリのプロモーションが含まれています。

シータ

気になる見出しをクリックして、
ぜひ最後までご覧ください。

弧度法とは？

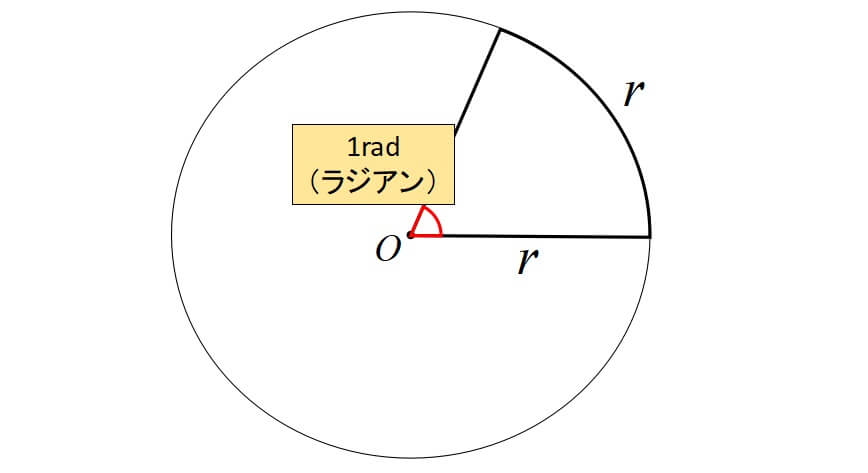
弧度法というのは、名前の通り”弧”に注目して角度を表現する方法のことです。

円の半径と弧の長さが等しくなる角度を1rad（ラジアン）といいます。

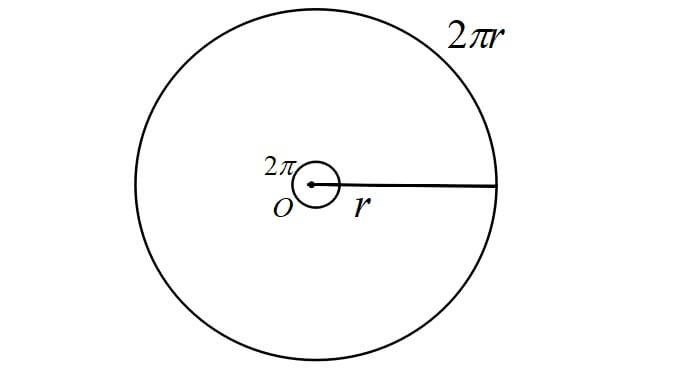
半径\(r\)の円において、円周の長さは\(2\pi r\)となり、この時の中心角を\(2\pi\)ラジアンといいます。

半円の場合は、円周の長さが\(\pi r\)なので、中心角は\(\pi\)ラジアンです。

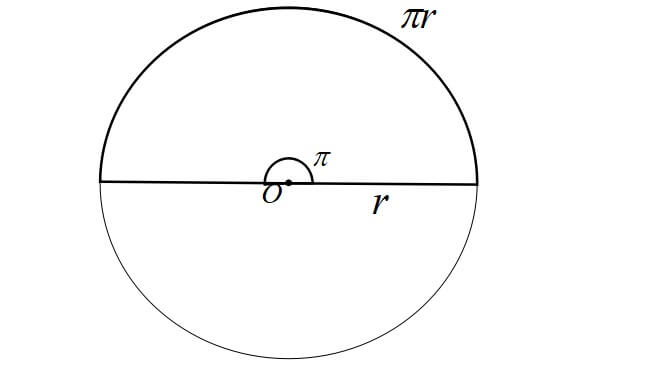
つまり、\(360^\circ=2\pi\),\(180^\circ=\pi\)です。

他の角度も弧度法に直したので確認してみてください。

三角関数まとめへ

弧度法と度数法の変換

弧度法を度数法に変換したり、逆に度数法から弧度法に変換したりできるようにしましょう。

ポイントは\(\pi=180^\circ\)であることです。

度数法から弧度法へ変換

まずは度数法から弧度法に直していきましょう。

\(180^\circ=\pi\)なので、

\(180^\circ\)を\(\pi\)に置き換えます。

つまり、\(180^\circ\)で割って\(\pi\)を掛けたら変換完成です。

\begin{eqnarray}
90^\circ &=& 90^\circ \div 180^\circ \times{\pi}\\
\displaystyle &=& 90^\circ \times \frac{\pi}{180^\circ}\\
\displaystyle &=& \frac{\pi}{2}
\end{eqnarray}

これで変換完成です。

練習問題を最後の章で用意しているので、ぜひ解いてみてください！

弧度法から度数法へ変換

次は弧度法から度数法へ変換します。

\(\pi=180^\circ\)なので、

\(\pi\)を\(180^\circ\)に置き換えます。

つまり、\(\pi\)に\(180^\circ\)を代入します。

\begin{eqnarray}
\displaystyle\frac{\pi}{3} &=& \frac{180^\circ}{3}\\
&=& 60^\circ
\end{eqnarray}

これで変換完成です。

こちらも練習問題を最後の章で用意しているので、ぜひ解いてみてください！

弧度法を使うメリット

なぜわざわざ弧度法を使うのか、弧度法のメリットを紹介します。

・弧度法のメリット１つ目は、弧の長さ，面積が簡単に求められます。

次の章「扇形の弧の長さと面積の公式」で解説するから分かるように、弧度法も用いると簡単に扇形の弧の長さと面積が求められるようになります。

扇形の弧の長さと面積の公式

つまり、扇形の弧の長さは（半径）×（中心角）で求められます。

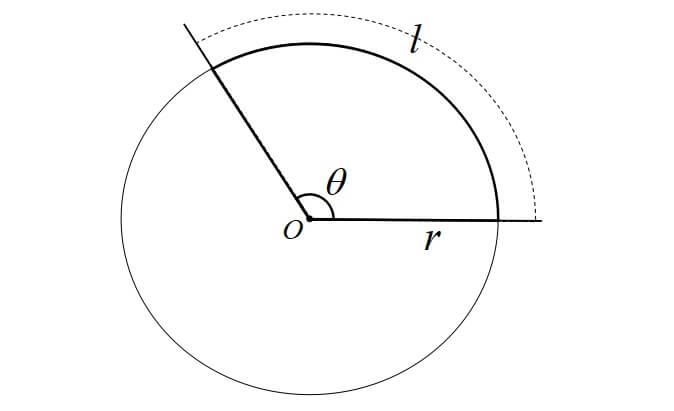
また、扇形の面積は\(\displaystyle \frac{1}{2}\)×\(（半径）^2\)

もしくは\(\displaystyle \frac{1}{2}\)×（半径）×（弧の長さ）で求めることができます。

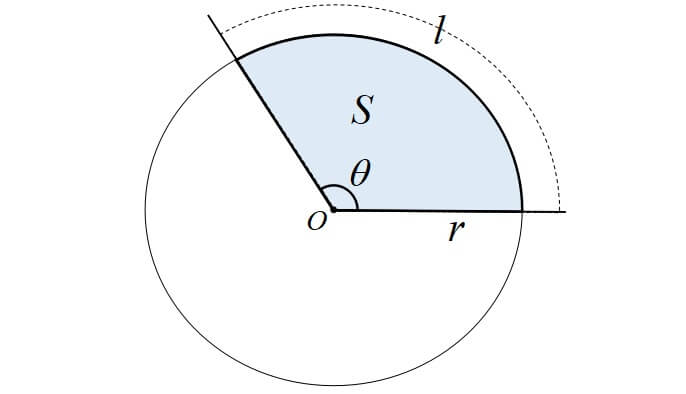
弧の長さと面積の公式　＜証明＞

弧の長さと面積の公式の証明をしておきます。

証明が必要ない方は、次の章へ進んでください。

【扇形の弧の長さ】

扇形の弧の長さは中心角の大きさに比例する。

中心角が２倍になれば、弧の長さも２倍になる。

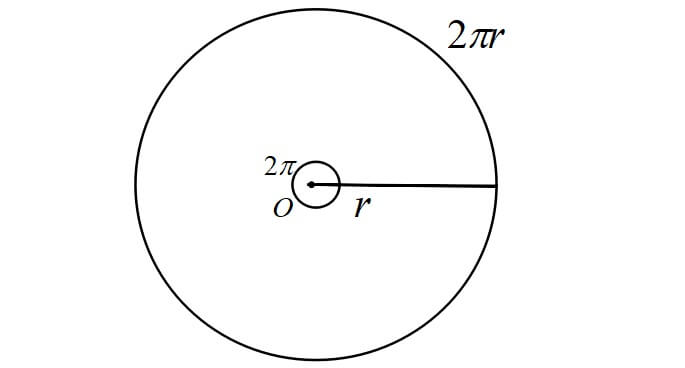
半径\(r\)の円周は\(2\pi r\)，中心角は\(2\pi\)だから比例式は

\[l:2\pi r=\theta:2\pi\]

これを計算すると、

\[2l\pi=2\pi r \theta\]

よって、\(l=r \theta\)となり証明終了です。

【扇形の面積】

面積も弧の長さと同様に比例式を使います。

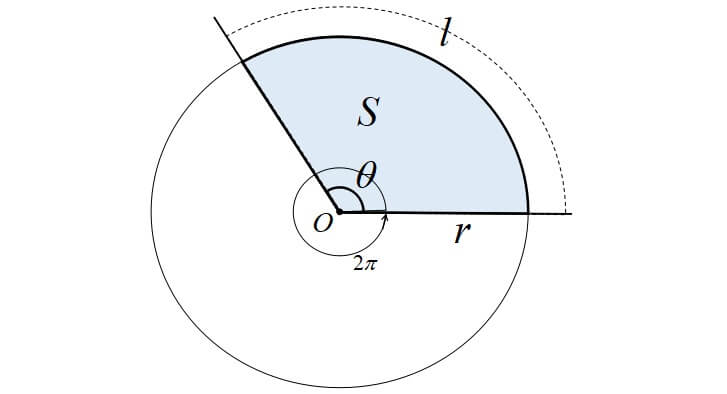
扇形の面積も中心角の大きさに比例するので，半径\(r\)の円の面積は\(\pi r^{2}\)，中心角\(2\pi\)なので

比例式　\(S:\pi r^{2}=\theta:2\pi\)

これを計算して、

\[2\pi S=\pi r^{2} \theta\]

\[\displaystyle S=\frac{1}{2} r^{2} \theta\]

\(l=r \theta\)なので

\[\displaystyle S=\frac{1}{2} r l\]

となり、証明終了です。

弧度法＜練習問題＞

解答

度数法から弧度法に直すときは、「\(180^\circ\)で割って\(\pi\)を掛ける」だったので、

《問題①》

\begin{eqnarray}
90^\circ &=& 90^\circ \div{180^\circ}\times{\pi}\\
&=& \displaystyle \frac{\pi}{2}
\end{eqnarray}

《問題②》

\begin{eqnarray}
45^\circ &=& 45^\circ \div{180^\circ}\times{\pi}\\
&=& \displaystyle \frac{\pi}{4}
\end{eqnarray}

《問題③》

\begin{eqnarray}
240^\circ &=& 240^\circ \div{180^\circ}\times{\pi}\\
&=& \displaystyle \frac{4}{3} \pi
\end{eqnarray}

解答

弧度法から度数法へ変換する場合は、\(\pi\)に\(180^\circ\)を代入しましたね！

《問題①》

\begin{eqnarray}
\displaystyle \frac{\pi}{4} &=& \frac{180^\circ}{4}\\
&=& 45^\circ
\end{eqnarray}

《問題②》

\begin{eqnarray}
\displaystyle \frac{2}{3} \pi &=& \frac{2}{3} \times{180^\circ}\\
&=& 120^\circ
\end{eqnarray}

《問題③》

\begin{eqnarray}
\displaystyle \frac{11}{6} \pi &=& \frac{11}{6} \times{180^\circ}\\
&=& 330^\circ
\end{eqnarray}

弧度法まとめ

今回は数学Ⅱの三角関数から弧度法の意味についてまとめました。

\(180^\circ\)が\(\pi\)に置き換わっただけなので、難しく考えないほうが良いでしょう。

では、ここまで読んでくださってありがとうございました。

みんなの努力が報われますように！

三角関数まとめへ