「三角関数の合成がよく分からない」
「何を表してるの?」
今回は三角関数の合成に関する悩みを解決します。
 高校生
高校生三角関数の合成が分かりません
以下が今回解説する三角関数の合成公式です。
[st-mybox title=”sinの合成公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a\)と\(b\)のいずれかが\(0\)でないとき
\[a \sin \theta+b \cos \theta=\sqrt{a^{2}+b^{2}} \sin (\theta+\alpha)\]
ただし, \(\alpha\)は\(\displaystyle \sin \alpha=\frac{b}{\sqrt{a^{2}+b^{2}}},\cos \alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\) を满たす角度とする。
[/st-mybox]
三角関数の合成って難しそうに見えますよね。
 シータ
シータ実はそんなことないよ!
公式の見た目は複雑ですが、証明や使い方は他と比べてもシンプルです。
ただ、入試でも使う重要な公式なので確実に抑えておきましょう。
本記事では三角関数の合成公式について解説しました。
図を用いて解説しているので、ぜひ最後までご覧ください。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
\(\sin\)の合成公式
まずは\(\sin\)の合成公式から解説します。
[st-mybox title=”sinの合成公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a\)と\(b\)のいずれかが\(0\)でないとき
\[a \sin \theta+b \cos \theta=\sqrt{a^{2}+b^{2}} \sin (\theta+\alpha)\]
ただし, \(\alpha\)は\(\displaystyle \sin \alpha=\frac{b}{\sqrt{a^{2}+b^{2}}},\cos \alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\) を满たす角度とする。
[/st-mybox]
\(\sin \theta+\cos \theta\)を\(\sin\)で合成するときは以下の三角形を描きます。
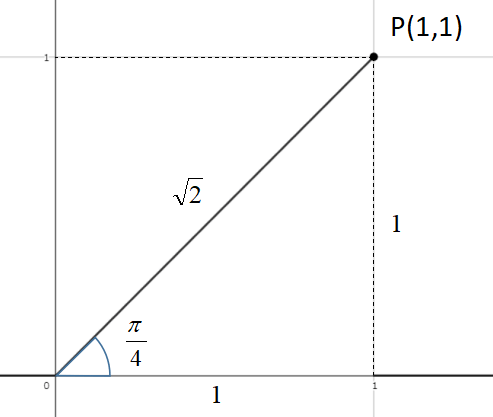
[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\sin \theta\)の係数⇒ 1
\(\cos \theta\)の係数⇒ 1
この場合は、(1,1)に点を打ちましょう。
[/st-mybox]
したがって、
\begin{eqnarray}
\displaystyle \sin \theta+\cos \theta&=&\sqrt{1^{2}+1^{2}}\sin \left(\theta+\frac{\pi}{4}\right)\\
&=&\sqrt{2}\sin \left(\theta+\frac{\pi}{4}\right)
\end{eqnarray}
となります。
座標平面上に点を取って、三角形をイメージすると解きやすくなります。
 高校生
高校生分かったような分からないような…
 シータ
シータ使い方の解説もしているからぜひ読んでみて。
\(\cos\)の合成公式
次は\(\cos\)の合成公式を紹介します。
[st-mybox title=”cosの合成公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a\)と\(b\)のいずれかが\(0\)でないとき
\[a \sin \theta+b \cos \theta=\sqrt{a^{2}+b^{2}} \cos (\theta-\beta)\]
ただし, \(\beta\)は\(\displaystyle \sin \beta=\frac{a}{\sqrt{a^{2}+b^{2}}},\cos \beta=\frac{b}{\sqrt{a^{2}+b^{2}}}\) を满たす角度とする。
[/st-mybox]
\(\sin \theta+\cos \theta\)を\(\cos\)で合成すると、
\begin{eqnarray}
\displaystyle \sin \theta+\cos \theta&=&\sqrt{1^{2}+1^{2}}\cos \left(\theta-\frac{\pi}{4}\right)\\
&=&\sqrt{2}\cos \left(\theta-\frac{\pi}{4}\right)
\end{eqnarray}
\(\sin\)の合成と異なり、かっこの中身がマイナスなので注意しましょう。
合成公式の証明
合成公式の証明には加法定理を使います。
[st-mybox title=”加法定理とは?” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
・三角関数の合成\(\sin\)
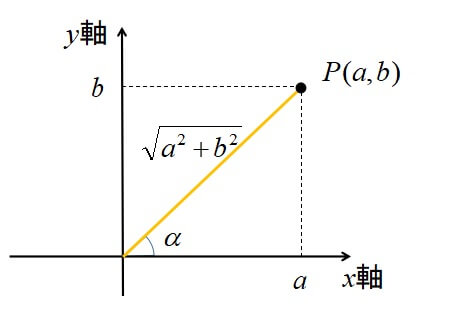
上図から以下のことがいえます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[r=\sqrt{a^{2}+b^{2}}\]
\[\displaystyle \sin α=\frac{b}{r} \Leftrightarrow b=r\sin α\]
\[\displaystyle \cos α=\frac{a}{r} \Leftrightarrow a=r\cos α\]
[/st-mybox]
ここで
\begin{eqnarray}
a \sin \theta + b \cos \theta&=&r\cos \alpha \sin \theta +r\sin \alpha \cos \theta\\
&=&r(\sin \theta \cos \alpha +\cos \theta \sin \alpha)\\
&=&r\sin (\theta + \alpha)\\
&=&\sqrt{a^{2}+b^{2}}\sin (\theta + \alpha)
\end{eqnarray}
よって、証明終了。
・三角関数の合成\(\cos\)
次は\(\cos\)の形をした合成の証明をします。
三角関数の合成は\(\sin\)の形にすることがほとんどですが、\(\cos\)の形にも変形できると考え方の幅が広がります。
\(a \sin \theta + b \cos \theta\)を用いて証明します。
\(\cos\)で合成するときは、点\(P(b,a)\)とします。
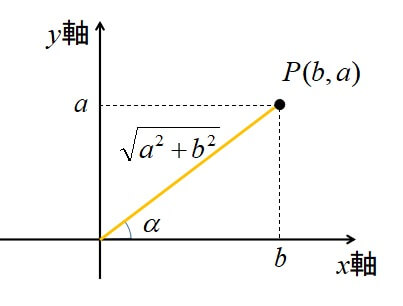
それによって、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[r=\sqrt{a^{2}+b^{2}}\]
\[\displaystyle \sin α=\frac{a}{r} \Leftrightarrow a=r\sin α\]
\[\displaystyle \cos α=\frac{b}{r} \Leftrightarrow b=r\cos α\]
[/st-mybox]
ここで、
\begin{eqnarray}
a \sin \theta + b \cos \theta&=&r\sin \alpha \sin \theta +r\cos \alpha \cos \theta\\
&=&r(\cos \theta \cos \alpha +\sin \theta \sin \alpha )\\
&=&r\cos (\theta – \alpha)\\
&=&\sqrt{a^{2}+b^{2}}\cos (\theta – \alpha)
\end{eqnarray}
よって、証明終了。
 高校生
高校生式変形して加法定理の形にしたんですね!
合成公式の使い方
三角関数の合成をどのように使うのか確認しましょう。
[st-mybox title=”例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\sqrt{3}\sin \theta+\cos \theta\)を,\(r\sin (\theta+\alpha)\)の形に变形せよ。
ただし, \(r>0,-\pi<\alpha<\pi\) とする.
[/st-mybox]
そして、合成する際の主な手順はこちら
[st-mybox title=”合成の手順” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 座標平面上に三角形を描く
- 三平方の定理で斜辺を求める
- 偏角を求める
- 合成公式に代入して完成
[/st-mybox]
それでは具体的に求めてみましょう。
解説
三角関数の合成をするために、斜辺と偏角を求めます。
\(\sqrt{3}\sin \theta+\cos \theta\)の合成なので、
\(x\)座標が\(\sqrt{3}\)、\(y\)座標が\(1\)の三角形を描きましょう。
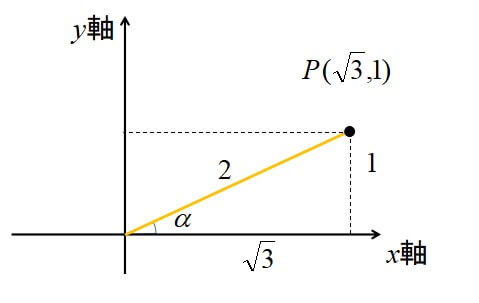
すると、斜辺\(r\)の長さは三平方の定理より、
\[r=\sqrt{\sqrt{3}^{2}+1^{2}}=2\]
これは偏角の大きさが\(\displaystyle \frac{\pi}{6}\)の三角形です。

三角形の斜辺の長さと偏角が分かりました。
したがって、
\[\displaystyle \sqrt{3} \sin \theta+\cos \theta=2 \sin (\theta + \frac{\pi}{6})\]
これで三角関数の合成ができました。
 高校生
高校生思ったよりも簡単でした!
 シータ
シータ与えられた式から図が書ければ簡単だね
三角関数の合成《練習問題》
三角関数の合成に挑戦してみましょう。
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の式を,\(r\sin (\theta+\alpha)\)の形に变形せよ。ただし, \(r>0,-\pi<\alpha<\pi\) とする。
(1) \(\sin \theta+\sqrt{3} \cos \theta\)
(2) \(\sin \theta-\cos \theta\)
[/st-mybox]
 シータ
シータ実際に手を動かして考えてみよう!
練習問題1の解説
\(\sin \theta+\sqrt{3} \cos \theta\)の合成を考えます。
まず、座標平面上に三角形を書きましょう。
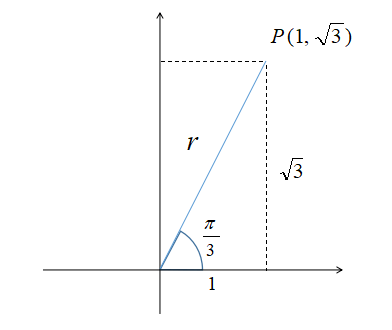
三平方の定理より、
\begin{eqnarray}
r&=&\sqrt{1^{2}+\sqrt{3}^{2}}\\
&=&2
\end{eqnarray}
図から偏角は\(\displaystyle \frac{\pi}{3}\)だと分かるので
\[\sin \theta+\sqrt{3} \cos \theta=2 \sin(\theta+\frac{\pi}{3})\]
練習問題2の解説
\(\sin \theta-\cos \theta\)の合成を考えます。
まず、座標平面上に三角形を書きましょう。
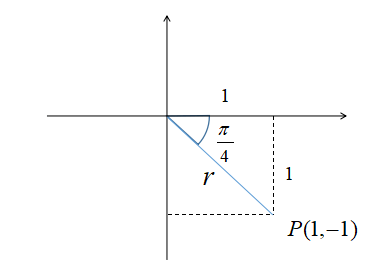
三平方の定理より、
\begin{eqnarray}
r&=&\sqrt{1^{2}+1^{2}}\\
&=&\sqrt{2}
\end{eqnarray}
図から偏角は\(\displaystyle -\frac{\pi}{4}\)だと分かるので
\[\sin \theta – \cos \theta=\sqrt{2} \sin(\theta-\frac{\pi}{4})\]
三角関数の合成 まとめ
今回は三角関数の合成についてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]三角関数の合成[/st-marumozi]
基本は\(\sin\)の合成公式を用いる。
[st-mybox title=”sinの合成公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a\)と\(b\)のいずれかが\(0\)でないとき
\[a \sin \theta+b \cos \theta=\sqrt{a^{2}+b^{2}} \sin (\theta+\alpha)\]
ただし, \(\alpha\)は\(\displaystyle \sin \alpha=\frac{b}{\sqrt{a^{2}+b^{2}}},\cos \alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\) を满たす角度とする。
[/st-mybox]
[st-mybox title=”合成の手順” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 座標平面上に三角形を描く
- 三平方の定理で斜辺を求める
- 偏角を求める
- 合成公式に代入して完成
[/st-mybox]
三角関数の合成には加法定理が使われていましたね。
今回は合成公式について解説しましたが、三角関数には重要な公式がたくさんあります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
三角関数の重要ポイントはこちらの記事でまとめました。
[st-card myclass=”” id=”2005″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[st-mybutton class=”” url=”https://math-travel.jp/sankakukansuu-matome/” title=”三角関数のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”100″ fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]

