「加法定理の公式が覚えられない」
「加法定理の語呂合わせが知りたい」
今回は加法定理に関するこんな悩みを解決します。
高校生毎回忘れてしまうので覚え方が知りたいです…
三角形の加法定理しっかりと覚えられていますか？
加法定理
\begin{eqnarray}
\sin(α+β)&=&\sin \alpha \cos \beta + \cos \alpha \sin \beta\\
\sin(α-β)&=&\sin α \cosβ-\cosα \sinβ\\
\cos(α+β)&=&\cos α \cosβ-\sinα \sinβ\\
\cos(α-β)&=&\cos α \cos β+\sinα \sinβ\\
\displaystyle \tan(α+β)&=&\frac{\tanα+\tanβ}{1-\tanα \tanβ}\\
\displaystyle \tan(α-β)&=&\frac{\tanα-\tanβ}{1+\tanα \tanβ}
\end{eqnarray}
「咲いたコスモス コスモス咲いた」など語呂合わせて覚えている方も多いのではないでしょうか？
本記事では加法定理の覚え方を語呂合わせで５つ紹介します。
自分が1番気に入った語呂合わせで覚えてしまいましょう！
記事の内容
※本ページは学習アプリのプロモーションが含まれています。
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
加法定理の公式
加法定理は三角関数の重要公式の１つです。
以下に加法定理の公式一覧をまとめました。
加法定理
\begin{eqnarray}
\sin(α+β)&=&\sin \alpha \cos \beta + \cos \alpha \sin \beta\\
\sin(α-β)&=&\sin α \cosβ-\cosα \sinβ\\
\cos(α+β)&=&\cos α \cosβ-\sinα \sinβ\\
\cos(α-β)&=&\cos α \cos β+\sinα \sinβ\\
\displaystyle \tan(α+β)&=&\frac{\tanα+\tanβ}{1-\tanα \tanβ}\\
\displaystyle \tan(α-β)&=&\frac{\tanα-\tanβ}{1+\tanα \tanβ}
\end{eqnarray}
加法定理の公式の重要ポイントをまとめた記事はこちら
加法定理の覚え方
加法定理は\(\sin\)などがたくさん並んでいて、覚えづらい公式ですね。
公式を丸暗記するのは大変なので、語呂合わせで覚えましょう。
加法定理の覚え方
- \(\sin\)の覚え方
- \(\cos\)の覚え方
- \(\tan\)の覚え方
まずはサインの加法定理から覚え方です。
符号が逆になることもないので、比較的覚えやすい公式です。
sinの加法定理
\[\sin(\alpha ± \beta)=\sin \alpha \cos \beta ± \cos \alpha \sin \beta\]
- 咲いたコスモス コスモス咲いた
- サチコ小林 小林サチコ
次にコサインの加法定理の覚え方です。
コサインの加法定理は左辺と右辺で符号が逆なので注意しましょう。
cosの加法定理
\[\cos(\alpha ± \beta)=\cos \alpha \cos \beta ∓ \sin \alpha \sin \beta\]
- コスモスコスモス 咲いた咲いた
- 雪やコンコン、毎日(マイナス) シンシン
最後にタンジェントの覚え方です。
タンジェントの加法定理は他の2つとは異なり、分数の形になります。
tanの加法定理
\[\displaystyle \tan(α±β)=\frac{\tanα ± \tanβ}{1-\tanα \tanβ}\]
・タンタタン いま立った
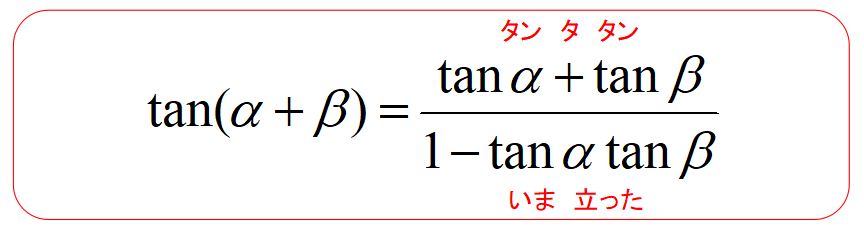
今回は左辺が加法のときの覚え方を解説しました。
左辺が減法（マイナス）のとき、右辺の符号も変わるので注意してください。
加法定理の証明
加法定理の覚え方を紹介しましたが、
「加法定理はどうしてそんな公式になるの？」
そう思う方もいるかもしれません。
加法定理の公式は、単位円上の2点の距離を用いて証明することができます。
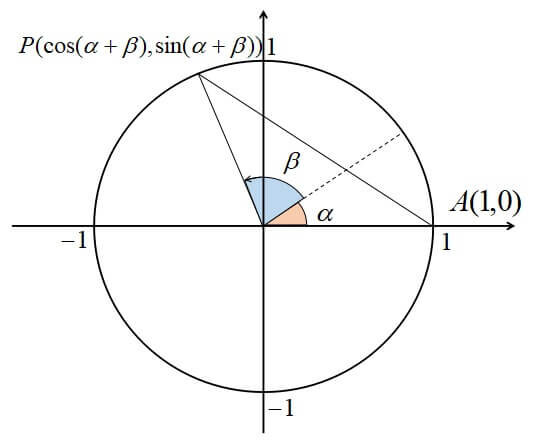
少し長い記事になってしまうので、加法定理の証明は別の記事でまとめました。
2倍角の公式
加法定理を活用した公式に“2倍角の公式”があります。
2倍角の公式
\begin{eqnarray}
\sin 2 \alpha&=&2 \sin \alpha \cos \alpha\\
\cos 2 \alpha&=&\cos^{2} \alpha – \sin^{2} \alpha\\
&=&1-2 \sin^{2} \alpha\\
&=&2 \cos^{2}-1\\
\displaystyle \tan 2\alpha&=&\frac{2 \tan \alpha}{1-\tan^{2}\alpha}
\end{eqnarray}
2倍角の公式は加法定理を活用して作ることができます。
\begin{eqnarray}
\sin 2 \alpha&=&\sin (\alpha + \alpha)\\
&=&\sin \alpha \cos \alpha + \cos \alpha \sin \alpha\\
&=&2\sin \alpha \cos \alpha
\end{eqnarray}
\begin{eqnarray}
\cos 2 \alpha&=&\cos (\alpha + \alpha)\\
&=&\cos \alpha \cos \alpha – \sin \alpha \sin \alpha\\
&=&\cos^{2} \alpha – \sin^{2} \alpha\\
&=&(1-\sin^{2} \alpha) – \sin^{2} \alpha\\
&=&1-2 \sin^{2} \alpha
\end{eqnarray}
2倍角の公式については別の記事で詳しくまとめました。
半角の公式
“半角の公式”は2倍角の公式を逆に活用した公式です。
半角の公式
\begin{eqnarray}
\sin ^{2} \frac{\alpha}{2}&=&\frac{1-\cos \alpha}{2}\\
\cos ^{2} \frac{\alpha}{2}&=&\frac{1+\cos \alpha}{2}\\
\tan ^{2} \frac{\propto}{2}&=&\frac{1-\cos \alpha}{1+\cos \alpha}
\end{eqnarray}
\(\cos \alpha\)が分かっていれば、\(\displaystyle \frac{\alpha}{2}\)に関する三角比を求めることができるのです。
半角の公式についてはこちら
加法定理《練習問題》
ここまで解説してきた加法定理を使って、練習問題に挑戦しましょう。
加法定理
次の値を求めよう。
(1)\(\sin 75^\circ\)
(2)\(\cos 15^\circ\)
(3)\(\tan 105^\circ\)
シータ公式に代入すれば解けちゃうよ！
練習問題1の解説
\(\sin 75^\circ\)は\(\sin(30^\circ + 45^\circ)\)の加法定理で求めます。
\begin{eqnarray}
\sin 75^\circ&=&\sin (30^\circ + 45^\circ)\\
&=&\sin30^\circ \cos45^\circ + \cos30^\circ \sin45^\circ\\
\displaystyle &=&\frac{1}{2} \times \frac{1}{\sqrt2} + \frac{\sqrt3}{2} \times \frac{1}{\sqrt2}\\
\displaystyle &=&\frac{\sqrt2}{4} + \frac{\sqrt6}{4}\\
\displaystyle &=&\frac{\sqrt2 + \sqrt6}{4}
\end{eqnarray}
練習問題2の解説
\(\cos 15^\circ\)は\(\cos(45^\circ – 30^\circ)\)の加法定理で求めます。
\begin{eqnarray}
\cos 15^\circ&=&\cos (45^\circ-30^\circ)\\
&=&\cos45^\circ \cos30^\circ+\sin45^\circ \sin30^\circ\\
\displaystyle &=&\frac{1}{\sqrt2} \times \frac{\sqrt3}{2}+ \frac{1}{\sqrt2} \times \frac{1}{2}\\
\displaystyle &=&\frac{\sqrt6}{4}+ \frac{\sqrt2}{4}\\
\displaystyle &=&\frac{\sqrt6+\sqrt2}{4}
\end{eqnarray}
練習問題3の解説
\(\tan 105^\circ\)は\(\tan(60^\circ + 45^\circ)\)の加法定理で求めます。
\begin{eqnarray}
\tan 105^\circ&=&\tan(60^\circ + 45^\circ)\\
\displaystyle &=&\frac{\tan 60^circ + \tan 45^\circ}{1-\tan 60^circ \tan 45^\circ}\\
\displaystyle &=&\frac{\sqrt{3}+1}{1-\sqrt{3} \times 1}\\
\displaystyle &=&\frac{\sqrt{3}+1}{1-\sqrt{3}}
\end{eqnarray}
高校生公式を覚えてしまえば代入するだけですね！
シータそうなんだよ！だからこそ加法定理はすぐに覚えてしまおう！
加法定理の覚え方 まとめ
今回は加法定理の覚え方についてまとめました。
加法定理の覚え方 まとめ加法定理
\begin{eqnarray}
\sin(α+β)&=&\sin \alpha \cos \beta + \cos \alpha \sin \beta\\
\sin(α-β)&=&\sin α \cosβ-\cosα \sinβ\\
\cos(α+β)&=&\cos α \cosβ-\sinα \sinβ\\
\cos(α-β)&=&\cos α \cos β+\sinα \sinβ\\
\displaystyle \tan(α+β)&=&\frac{\tanα+\tanβ}{1-\tanα \tanβ}\\
\displaystyle \tan(α-β)&=&\frac{\tanα-\tanβ}{1+\tanα \tanβ}
\end{eqnarray}
加法定理の覚え方を5つ紹介しました。
加法定理の覚え方
\[\sin(\alpha ± \beta)=\sin \alpha \cos \beta ± \cos \alpha \sin \beta\]
- 咲いたコスモス コスモス咲いた
- サチコ小林 小林サチコ
\[\cos(\alpha ± \beta)=\cos \alpha \cos \beta ∓ \sin \alpha \sin \beta\]
- コスモスコスモス 咲いた咲いた
- 雪やコンコン、毎日(マイナス) シンシン
\[\displaystyle \tan(α±β)=\frac{\tanα ± \tanβ}{1-\tanα \tanβ}\]
・タンタタン いま立った
加法定理を使うことで、\(45^\circ\)や\(60^\circ\)以外の三角比を求めることができます。
加法定理の重要ポイントはこちらの記事にまとめました。
コメント