[mathjax]
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 30px”]
「ベクトルの内積ってなに?」
「内積の公式や求め方が知りたい」
[/st-mybox]
今回は数学Bのベクトルから「ベクトルの内積」に関するこんな悩みを解決します。
 高校生
高校生ベクトルを習い始めたばかりで…
ベクトルには“内積”というものがあり、内積によって2つのベクトルがなす角の大きさが分かります。
[st-mybox title=”ベクトルの内積公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2つのベクトル\(\vec{a}\)、\(\vec{b}\)があり、2つのベクトルの始点同士を繋いでできた角をθとします。

\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta \cdots ①\]
\[\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2} \cdots ②\]
[/st-mybox]
ベクトルの内積はとても重要な公式なので、今回で必ず理解しておきましょう。
本記事ではベクトルの内積の公式や求め方について解説していきます。
また、記事下ではベクトルの重要公式についても説明しているので、合わせて参考にしていただければと思います!
 シータ
シータベクトルが苦手な方は
ぜひ最後までご覧ください。
それではベクトルの内積について解説していきましょう。
ベクトルの内積とは?
2つのベクトル\(\vec{a}\)、\(\vec{b}\)があり、2つのベクトルの始点同士を繋いでできた角をθとします。

このとき、\(\vec{a}\)と\(\vec{b}\)の内積は以下のように定義します。
[st-midasibox title=”ベクトルの内積” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\]
[/st-midasibox]
ベクトルの大きさ同士を掛けて、あいだの角の\(\cos \theta\)を掛けるため、
\(|\vec{a}|=0\) もしくは \(|\vec{b}|=0\)のとき
\[\vec{a} \cdot \vec{b}=0\]
となります。
平面ベクトルの内積公式
ベクトルの内積公式の定義を記載しましたが、「具体的にどう使うの?」とまだイメージが湧かないと思います。
ここからは内積に関係する公式を解説していきます。
①角度cosを使う公式(定義)
内積の公式の1つは、先ほど解説した定義です。

[st-midasibox title=”ベクトルの内積公式①” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
0ではない2つのベクトル\(\vec{a}\)、\(\vec{b}\)の始点同士をつないでできる角をθとします。
\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\]
[/st-midasibox]
②成分表示を使う公式
内積の公式はもう1つあり、成分表示を使って内積を表すこともできます。
[st-midasibox title=”ベクトルの内積公式②” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
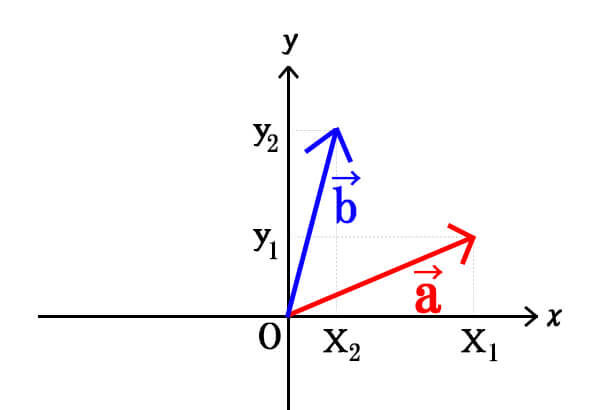
\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)とすると、
\[\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2}\]
[/st-midasibox]
平面ベクトルの内積を求める
先ほど紹介した公式をもとに、平面ベクトルの内積を求めてみましょう。
[st-mybox title=”平面ベクトルの内積:例題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
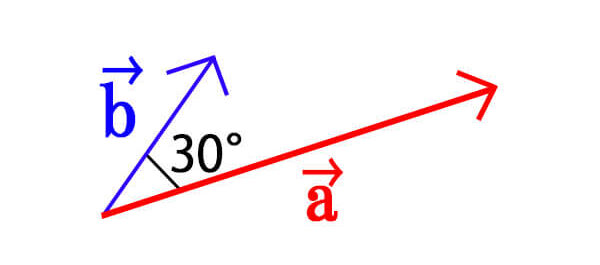
\(|\vec{a}|=2,|\vec{b}|=1\)、また\(\vec{a},\vec{b}\)の始点同士を繋いでできる角をθとして、\(\theta=30°\)であるとき、\(\vec{a}\)と\(\vec{b}\)の内積\(\vec{a} \cdot \vec{b}\)を求めよ。
[/st-mybox]
解答をチェックする
\(\vec{a}\)と\(\vec{b}\)の内積は、
\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\]
であるから、
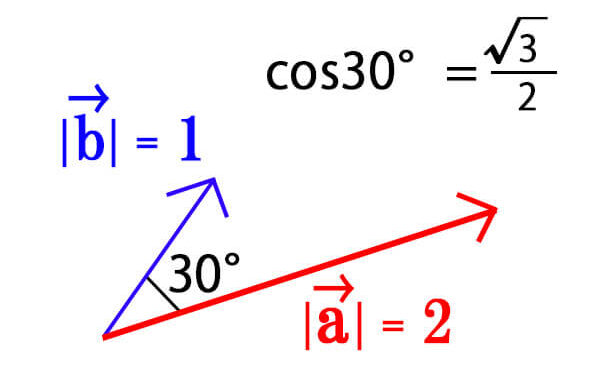
\[\displaystyle \vec{a} \cdot \vec{b}=2 \times 1 \times \frac{\sqrt{3}}{2}\]
よって、
\[\vec{a} \cdot \vec{b}=\sqrt{3}\]
[st-mybox title=”平面ベクトルの内積:例題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
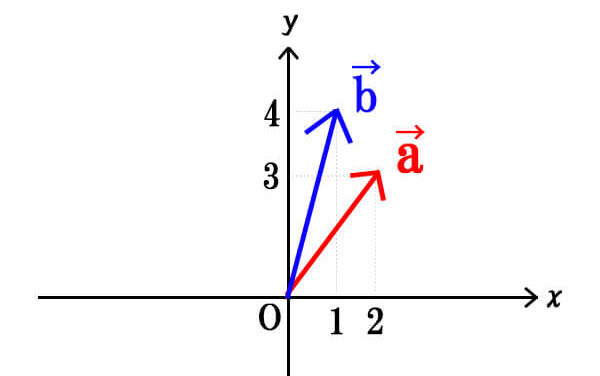
\(\vec{a}=(2,3),\vec{b}=(1,4)\)のとき、\(\vec{a}\)と\(\vec{b}\)の内積\(\vec{a} \cdot \vec{b}\)を求めよ。
[/st-mybox]
[st-slidebox fontawesome=”fa-check” text=”解答をチェックする” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]
こちらも内積の公式に代入して
\[\vec{a} \cdot \vec{b}=2 \times 1+3 \times 4=14\]
[/st-slidebox]
空間ベクトルの内積公式
先ほどは平面ベクトルの内積に関する公式を解説しました。
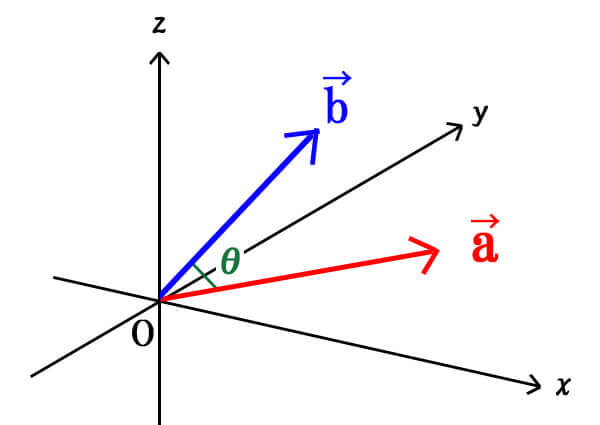
ここからは、空間ベクトルの内積に関する公式を解説していきます。
 シータ
シータ難しく見えますが、考え方は平面ベクトルの時と同じなので安心してください!
①角度cosを使う公式(定義)
0ではない2つのベクトル\(\vec{a}\)、\(\vec{b}\)の始点同士を繋いでできる角をθとします。

[st-midasibox title=”空間ベクトルの内積公式①” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\]
[/st-midasibox]
これは平面ベクトルの時と同じということですね!
②成分表示を使う公式
先ほど角度\(\cos\)を使う公式は、平面ベクトルの時と同じでしたが、成分表示を使う際は少し注意が必要です。
というのも、空間ベクトルになると成分が1つ増えるからです。
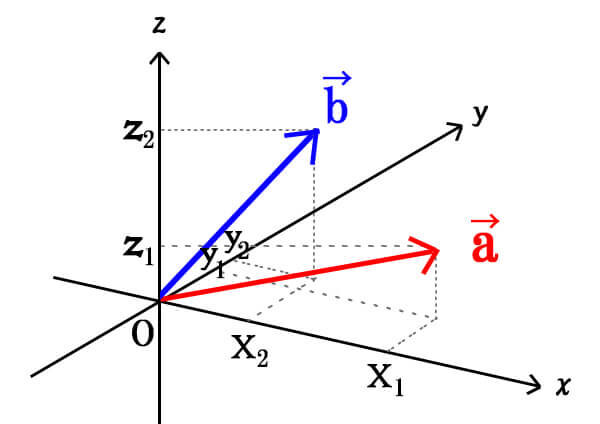
成分表示を使った、空間ベクトルの内積は以下のように表されます。
[st-midasibox title=”空間ベクトルの内積公式②” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\(\vec{a}=(x_{1},y_{1},z_{1}),\vec{b}=(x_{2},y_{2},z_{2})\)とすると、
\[\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}\]
[/st-midasibox]
空間ベクトルの内積を求める
先ほどの公式を使って、空間ベクトルの内積を求めましょう。
[st-mybox title=”空間ベクトルの内積:例題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(\vec{a}=(1,2,3),\vec{b}=(2,2,1)\)のとき、\(\vec{a}\)と\(\vec{b}\)の内積\(\vec{a} \cdot \vec{b}\)を求めよ。
[/st-mybox]
[st-slidebox fontawesome=”fa-check” text=”解答をチェックする” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]
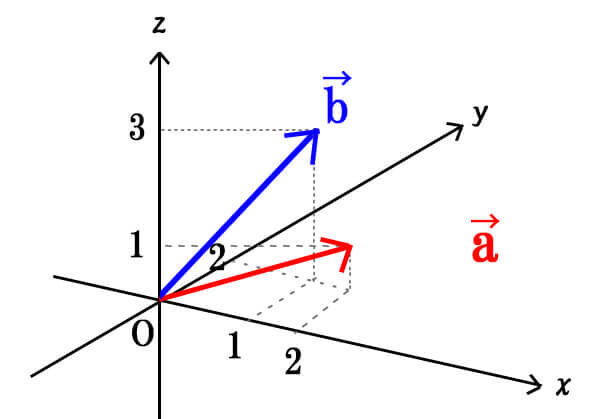
先ほどの公式をもとに当てはめると、
\[\vec{a} \cdot \vec{b}=1 \times 2+2 \times 2+3 \times 1=9\]
[/st-slidebox]
平面ベクトルの時も空間ベクトルの時も、基本的な考え方は同じであることが分かりますね!
ベクトルの内積の活用
ここからはベクトルの内積を用いた重要公式について解説します。
 シータ
シータ理解できれば、解ける問題の幅が広がりますよ!
内積の垂直条件
まずはベクトルの垂直条件を紹介します。
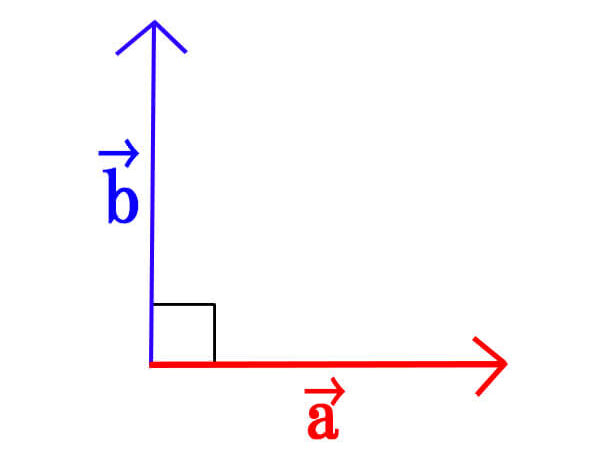
ここに0ではない2つのベクトル\(\vec{a},\vec{b}\)があります。
[st-mybox title=”垂直条件” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a},\vec{b}\)が垂直に交わるとき
\[\vec{a} \cdot \vec{b}=0\]
[/st-mybox]
簡単な証明としては内積の定義から、
\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\)であり、
垂直であるとき、\(\cos \theta=0\)となり、垂直条件が成り立ちます。
\(\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2}=0 \)も成り立ちます。
内積の平行条件
次は平行なときの条件を紹介します。
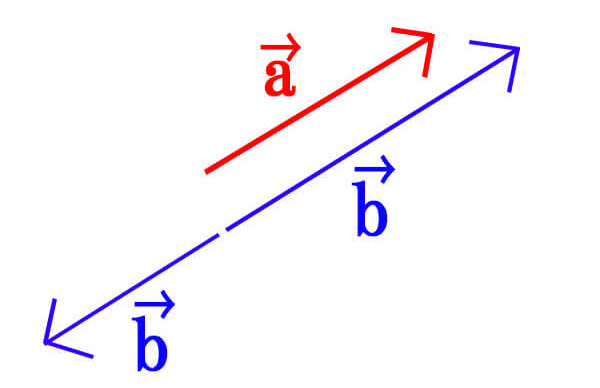
0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)があるとき、
[st-mybox title=”垂直条件” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a},\vec{b}\)が平行のとき
\(\vec{a} // \vec{b}=k \vec{a}\)となる実数kがある。
また、\(\vec{a} // \vec{b}=x_{1}y_{2}-x_{2}y_{1}=0\)も成り立つ。
[/st-mybox]
詳しく解説します。

画像を見ると分かりやすく、
\(\vec{a} // \vec{b}\)のとき、\(\vec{b}=k \vec{a}\)(kは実数)と表せる。…③
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”0″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
kの値が0より大きいときは、\(\vec{a}\)と\(\vec{b}\)は同じ向きに平行、
kの値が0より小さいときは、\(\vec{a}\)と\(\vec{b}\)は逆向きに平行です。
[/st-mybox]
次に、\(\vec{a} // \vec{b}\)のとき、\(x_{1}y_{2}-x_{2}y_{1}=0\)についてみていきましょう。
ベクトルの成分表示を使って
\((x_{2},y_{2})=k (x_{1},y_{1})\)となるから、\(x_{2}=kx_{1},y_{2}=ky_{1}\)
ここから比を考えると、\(x_{2}:y_{2}=kx_{1}:ky_{1}\)となります。
さらに、比の性質を使えば、\(x_{2}:y_{2}=x_{1}:y_{1}\)が成り立つことが分かります。
よって、\(x_{1}y_{2}-x_{2}y_{1}=0\)となります。
ベクトルの内積公式 証明
ベクトルの内積公式の証明をしていきます。
[st-mybox title=”ベクトルの内積公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2つのベクトル\(\vec{a}\)、\(\vec{b}\)があり、2つのベクトルの始点同士を繋いでできた角をθとします。

\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta \cdots ①\]
\[\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2} \cdots ②\]
[/st-mybox]
①に関しては内積の定義なので、そういうものだとして覚えましょう。
②の成分表示を使う公式の証明は、余弦定理を使います。
0ではない2つのベクトル\(\vec{a}=\vec{OA},\vec{b}=\vec{OB}\)があり、この2つのベクトルがなす角をθとする。このとき、\(\angle{AOB}=\theta\)とおく。

このとき、\(\triangle{OAB}\)に余弦定理を使うと、
\[{AB}^2={OA}^2+{OB}^2-2 OA\times OB\times \cos \theta\]
図より、
\(AB=|\vec{b}-\vec{a}|、OA=|\vec{a}|、OB=|\vec{b}|\)であるから、
①の式は
\[|\vec{b}-\vec{a}|^2=|\vec{a}|^2+|\vec{b}|^2-2ab \cos \theta\]
また、\(\vec{b}-\vec{a}=(x_{2}-x_{1},y_{2}-y_{1})\)より、
\(AB=|\vec{b}-\vec{a}|=\sqrt{{(x_{2}-x_{1})}^2+{(y_{2}-y_{1})}^2}\)であるから、
\({(x_{2}-x_{1})}^2+{(y_{2}-y_{1})}^2={x_{1}}^2+{y_{1}}^2+{x_{2}}^2+{y_{2}}^2-2|\vec{a}||\vec{b}| \cos \theta\)
となる。
ここで両辺を整理すると、
\[|\vec{a}||\vec{b}| \cos \theta=x_1x_2+y_1y_2\]
となる。
したがって、\(\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2}\)
ベクトルの内積 まとめ
今回はベクトルの内積について学習しました。
平面ベクトルの・空間ベクトル両方で内積について考えましたが、まず平面ベクトルから理解を進めると分かりやすいですよ!
[st-mybox title=”ベクトルの内積公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2つのベクトル\(\vec{a}\)、\(\vec{b}\)があり、2つのベクトルの始点同士を繋いでできた角をθとします。

\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta \cdots ①\]
\[\vec{a} \cdot \vec{b}=x_{1}x_{2}+y_{1}y_{2} \cdots ②\]
[/st-mybox]
この成分表示を使えば、足し算・引き算など計算もスムーズにできます。
ぜひ活用して、ベクトルへの理解を深めてくださいね!
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

