[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 30px”]
「ベクトルの成分表示ってなに?」
「成分表示はどうやって求めるの?」
[/st-mybox]
今回は数学Bのベクトルから「ベクトルの成分表示」に関するこんな悩みを解決します。
 高校生
高校生ベクトルを習い始めたばかりで…
ベクトルには成分があり、始点と終点の差がそのままベクトルの成分となります。
[st-midasibox title=”成分表示の表し方” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\(\vec{a}\)=(x軸方向に進んだ距離,y軸方向に進んだ距離)
[/st-midasibox]
ベクトルの重要公式には成分表示を活用するものが多いため、今回で必ず理解しておきましょう。
本記事ではベクトルの成分表示の求め方について解説していきます。
また、記事下ではベクトルの重要公式についても説明しているので、合わせて参考にしていただければと思います!
 シータ
シータ入塾を検討している方は
ぜひ最後までご覧ください。
それではベクトルの成分表示について解説していきましょう。
[st_af id=”13737″]
ベクトルの成分表示とは?
ベクトルの成分表示の前に、まず「ベクトルとは何か?」を復習しましょう。
ベクトルとは「大きさ」と「向き」を持った矢印です。
そして、そのベクトルがどっちの向きに、どのくらいの大きさを持っているのかを示すときに“成分表示”を使うことがあります。
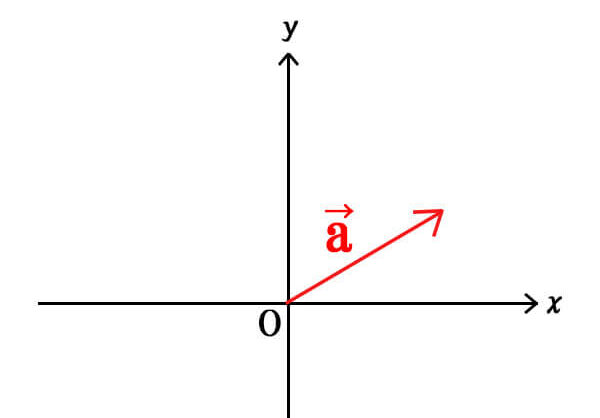
例えば、下画像のベクトルを考えてみましょう。
(ここではまず分かりやすいように座標平面上で考えてみます)

xy平面上に\(\vec{a}\)があり、ベクトルの始まりを“始点”、終わりを“終点”とします。
始点から終点に向けて、x軸方向、y軸方向にそれぞれどれだけ進んだかを考え、
[st-midasibox title=”成分表示の表し方” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\(\vec{a}\)=(x軸方向に進んだ距離,y軸方向に進んだ距離)
[/st-midasibox]
という風に表します。
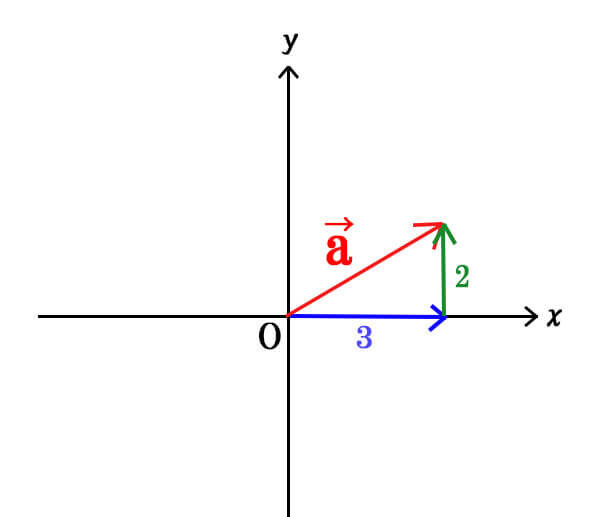
画像の\(\vec{a}\)はx軸方向に進んだ距離は3、y軸方向に進んだ距離は2となるため、
\[\vec{a}=(3,2)\]
と表されます。
[st-cmemo myclass=”st-text-guide st-text-guide-attention” fontawesome=”fa-exclamation-circle” iconcolor=”#ef5350″ bgcolor=”#ffebee” color=”#000000″ bordercolor=”#ffcdd2″ borderwidth=”” iconsize=””]
ただし、これはベクトルの動きを表しただけで、座標とは異なるので注意してください。
[/st-cmemo]
ベクトルの成分表示の求め方
ここでは、例題を使ってベクトルの成分表示を求めてみます。
少しずつ解説していきますので「難しそう…」と感じている方も安心してくださいね!
平面ベクトルの成分
まずは、平面ベクトルの成分表示です。
平面ベクトルとは、2つの成分で表すことができるものです。
先ほど解説したものも、平面ベクトルと言われているものです。
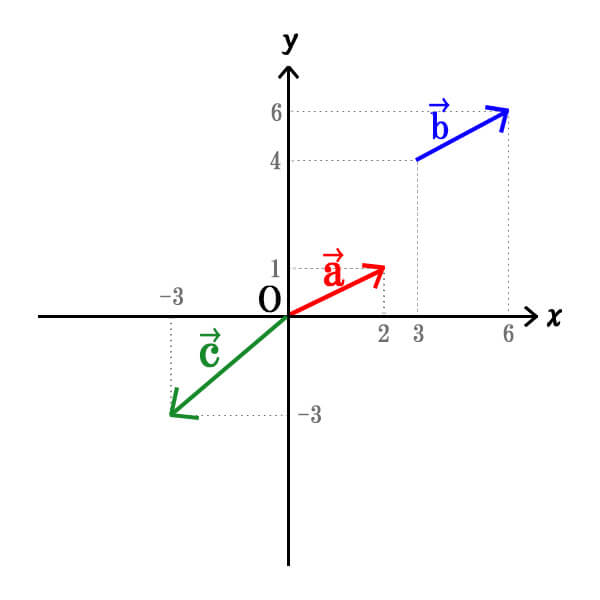
画像上にある\(\vec{a},\vec{b},\vec{c}\)を成分表示してみましょう。
先ほど解説したように、ベクトルの成分は、始点から終点に向けて、x軸方向にどれだけ進んだか、y軸方向にどれだけ進んだかを考えるとうまくいきます。
まずは\(\vec{a}\)を求めます。
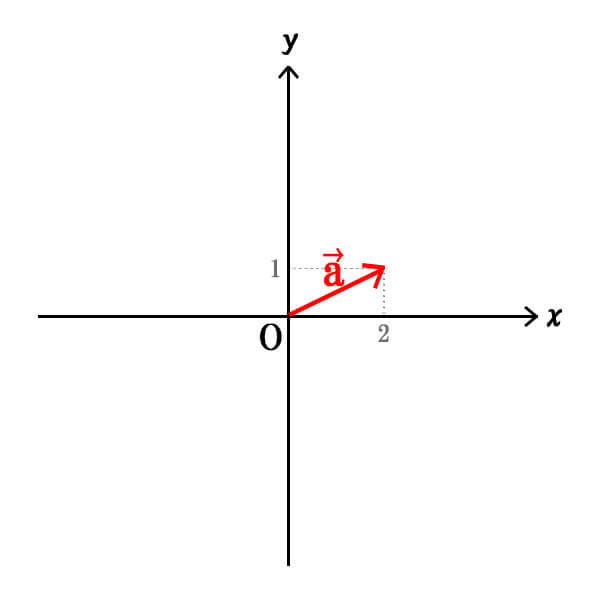
\(\vec{a}\)は始点から終点に向けて、x軸方向にどれだけ進んだか、y軸方向にどれだけ進んだかを考えると、\(\vec{a}=(2,1)\)となります。
次は、\(\vec{b}\)を求めてみましょう。
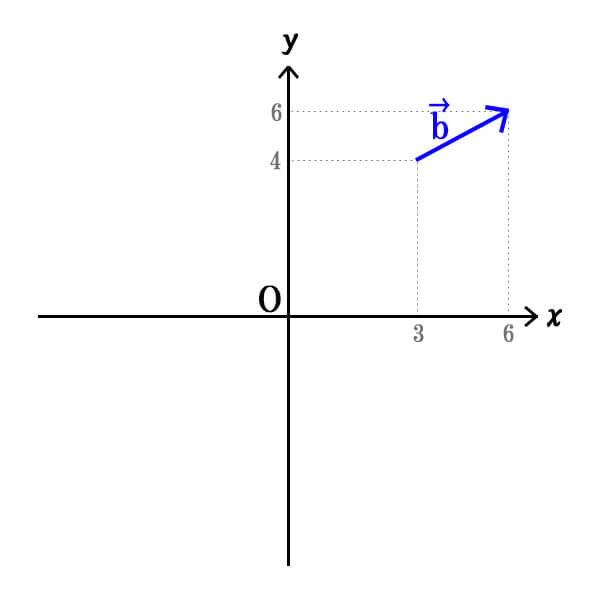
\(\vec{b}\)で間違えやすい解答が、\(\vec{b}=(6,6)\)です。
ここで注目するべきポイントは始点の位置で、\(\vec{a}\)と違って始点が原点でないため注意が必要です。
\(\vec{b}\)は始点\((x,y)=(3,4)\) 、終点\((x,y)=(6,6)\) なので、始点から終点に向けてx軸方向に3、y軸方向に2だけ進んでいることが分かります。
よって、\(\vec{b}=(3,2)\)となります。
最後に、\(\vec{c}\)を求めてみましょう。
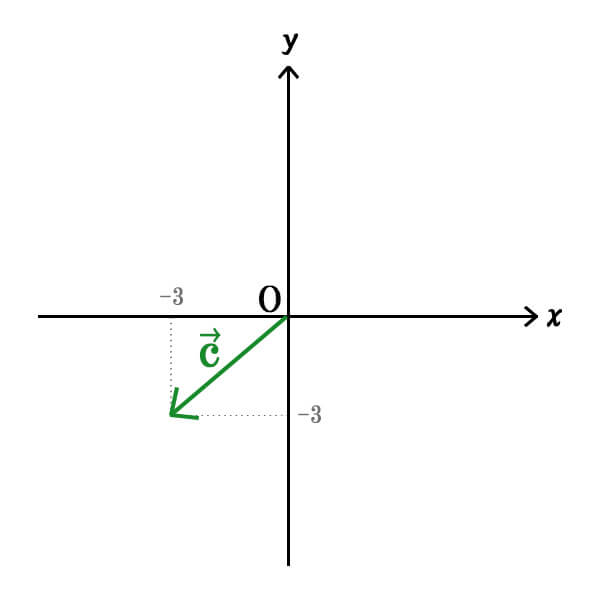
\(\vec{c}\)はこれまでのベクトルと向きが違いますね。
\(\vec{c}\)の始点・終点は、それぞれ始点\((x,y)=(0,0)\)、終点\((x,y)=(−3,−3)\)ですね。
それぞれ始点から終点に向けて、x軸方向に-3、y軸方向に-3進んでいることが分かります。
よって、\(\vec{c}=(−3,−3)\)となります。
空間ベクトルの成分
ここからは、空間ベクトルを考えます。
空間ベクトルでも考え方は平面と同じなので安心して下さい!
空間ベクトルとなると軸が1つ増えるので、3つの成分で表すことになります。
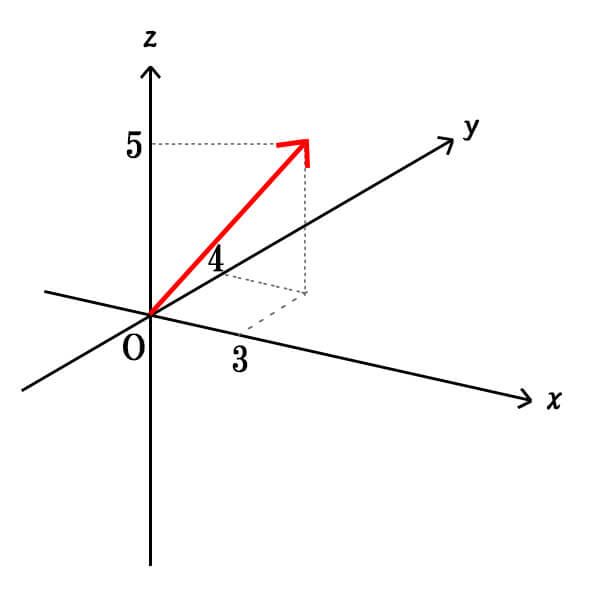
始点は原点で、終点は\((x,y,z)=(3,4,5)\)となっています。
平面ベクトルの時と同様に、始点から終点に向けて、どのくらい進んだかを考えてみます。
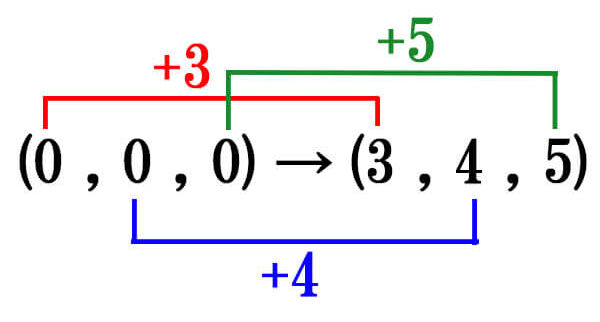
すると、\(\vec{a}=(3,4,5)\)となることが分かるでしょう。
ベクトルの成分を求める《練習問題》
ベクトルの成分表示を求める練習をしてみましょう!
[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a},\vec{b}\)の成分を求めてみましょう。
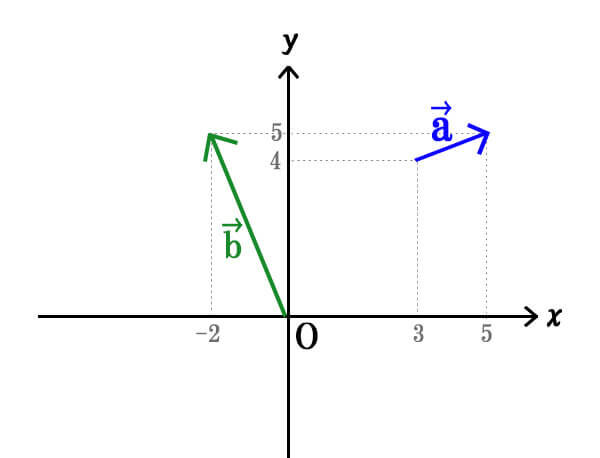
[/st-mybox]
解答を確認する
[st-mybox title=”解答” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”0″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a}=(2,1)、\vec{b}=(−2,5)\)
[/st-mybox]
解説:
\(\vec{a}\)の始点は\((x,y)=(3,4)\)、終点は\((x,y)=(5,5)\)
始点から終点に向けて、どのくらい進んだかを考えると、\(\vec{a}=(2,1)\)となります。
\(\vec{b}\)の始点は\((x,y)=(0,0)\)、終点は\((x,y)=(−2,5)\)
始点から終点に向けて、どのくらい進んだかを考えると、\(\vec{b}=(−2,5)\)となります。
[st-mybox title=”練習問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{c}\)の成分を求めてみましょう。
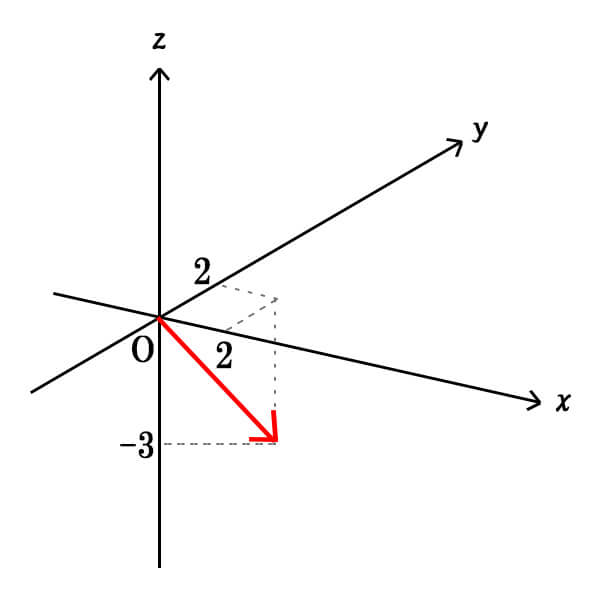
[/st-mybox]
[st-slidebox fontawesome=”fa-check” text=”解答を確認する” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]
[st-mybox title=”解答” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”0″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{c}=(2,2,−3)\)
[/st-mybox]
解説:
\(\vec{c}\)の始点は\((x,y,z)=(0,0,0)\)、終点は\((x,y,z)=(2,2,−3)\)
始点から終点に向けて、どのくらい進んだかを考えると、\(\vec{c}=(2,2,−3)\)となります。
[/st-slidebox]
ベクトルの成分を使った公式
ここからは、ベクトルの成分を使った重要公式をいくつか紹介します。
知っておくと解ける問題の幅が広がり、ベクトル分野が少し得意に近づくこと間違いなし!
ベクトルの大きさ
ベクトルには“大きさ”があり、成分を使って求めることができます。
[st-midasibox title=”ベクトルの大きさ” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\(\vec{a}=(x,y)\)とするとき、\(\vec{a}\)の大きさは
\[|\vec{a}|=\sqrt{x^2+y^2}\]
[/st-midasibox]
中学で習った三平方の定理を使うと理解しやすいですね。
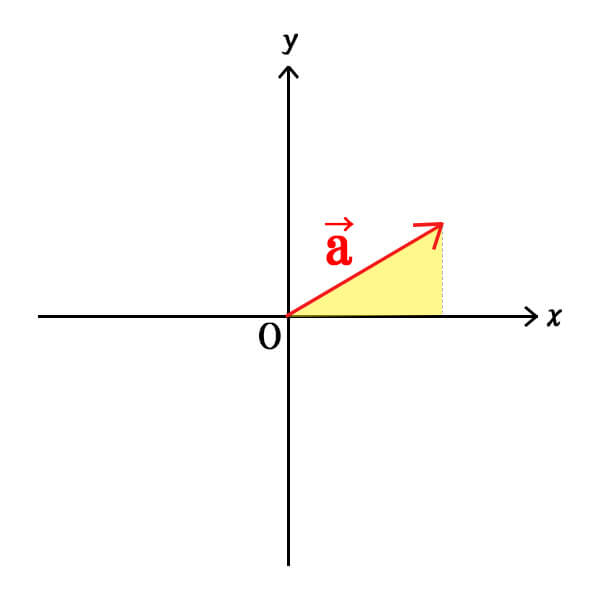
ベクトルの足し算・引き算
ベクトルの成分同士を、足したり引いたりすることもできます。
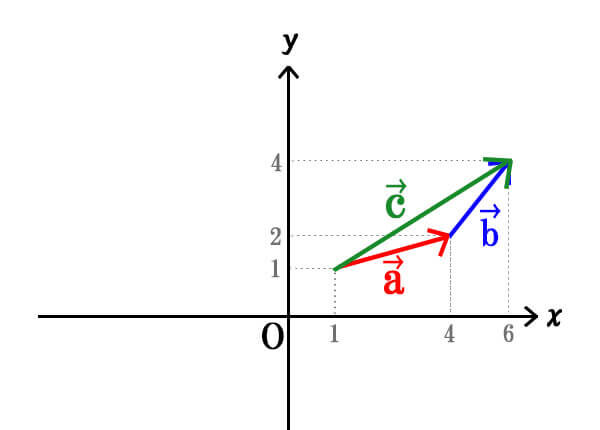
\(\vec{a}=(3,1)、\vec{b}=(2,2)\)として、
\(\vec{c}=\vec{a}+\vec{b}=(3+2,2+1)=(5,3)\)
図で見ても\(\vec{c}\)の成分表示に一致していることが分かります。
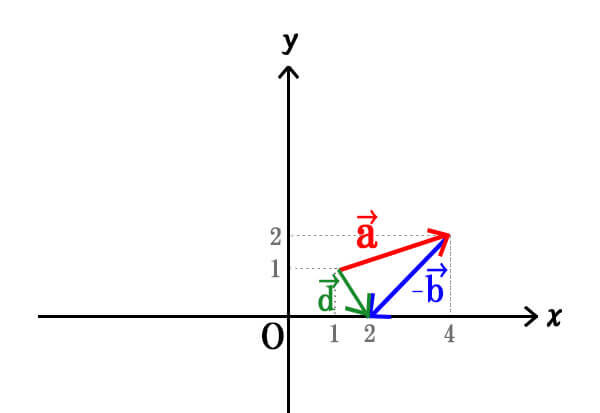
\(\vec{a}=(3,1)、\vec{b}=(2,2)\)
\(\vec{d}=\vec{a}+\vec{−b}=\vec{a}−\vec{b}=(3−2,1−2)=(1,−1)\)
図で見ても\(\vec{d}\)の成分表示に一致していることが分かります。
ベクトルの内積
ベクトルの成分を使えば、内積を求めることもできます。
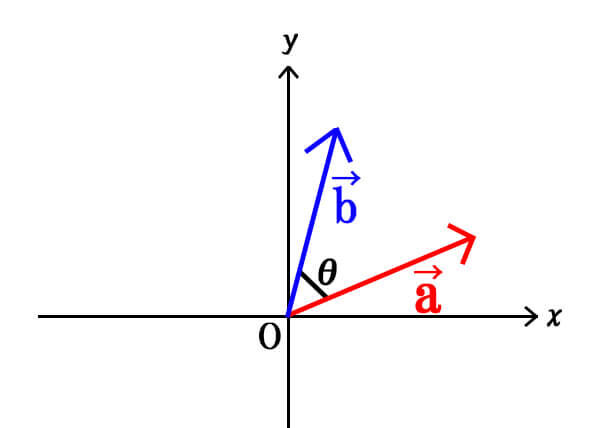
[st-midasibox title=”ベクトルの内積” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
\(\vec{a}=(x_{1},y_{1})、\vec{b}=(x_{2},y_{2})\)とするとき、
内積\(\vec{a} \cdot \vec{b}\)は、
\[\vec{a} \cdot \vec{b}=x_1x_2+y_1y_2\]
と表す。
[/st-midasibox]
ベクトルの成分表示 まとめ
今回はベクトルの成分表示について解説していきました。
成分表示自体はそこまで難しいものではないです。
しかし、成分表示を用いた重要公式が多いため、ベクトルの成分表示は必ず習得して欲しいです。
[st-minihukidashi fontawesome=”” fontsize=”” fontweight=”” bgcolor=”#FFB74D” color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]ベクトルの成分表示[/st-minihukidashi]
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#03A9F4″ bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
ベクトルの成分の求め方は始点から終点に向けて、x軸方向、y軸方向にどれだけ進んだかを考え、
\(\vec{a}\)=(x軸方向に進んだ距離,y軸方向に進んだ距離)
と表します。
[/st-mybox]
この成分表示を使えば、足し算・引き算など計算もスムーズにできます。
ぜひ活用して、ベクトルへの理解を深めてくださいね!
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
>>ベクトルの大きさの求め方!なぜ2乗の公式で求められるの?
[/st-mybox]
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

