三角比の相互関係を使いこなそう！必ず覚えたい３つの重要公式

数学Ⅰ三角比のなかでも「三角比の相互関係」はかなり重要な公式です。

本記事では、三角比の相互関係についてまとめていきます。

三角比の単元には重要公式が多くありますが、その中でも三角比の相互関係は必ず覚えて欲しい公式です。

この相互関係は数Ⅱの「三角関数」でも使うので、この機会に必ず覚えましょう。

とはいえ、初めは使い方もよく分からないですよね。ぼくも完璧に覚えられるまでは何度も調べてました

本記事では三角比の相互関係を丁寧に解説しているのでぜひ最後までご覧ください。

※本ページは学習アプリのプロモーションが含まれています。

三角比の相互関係

三角比の相互関係は必ず押さえておきたい重要な公式です。

三角比の相互関係を使うメリットとしては、sin,cos,tanのどれか1つが分かれば他の全てを求めることができることです。

それでは三角比の相互関係の使い方について解説していきます。

三角比の相互関係　使い方

三角比の相互関係を使って実際に各値を求めてみましょう。

下部に例題3つを用意したのでそれぞれの使い方を確認してください。

\(\sin^{2} \theta+\cos^{2} \theta=1\)

この公式は、\(\sin \theta\)もしくは\(\cos \theta\)が分かるときに使う公式です。

例えば\(\theta\)が鋭角で\(\displaystyle \sin \theta=\frac{1}{3}\)だとしましょう。

このとき三角比の相互関係①を用いて、

\[\sin^{2} \theta+\cos^{2} \theta=1\]

\[\displaystyle (\frac{1}{3})^{2}+\cos^{2} \theta=1\]

\[\displaystyle \frac{1}{9}+\cos^{2} \theta=1\]

\[\displaystyle \cos^{2} \theta=\frac{8}{9}\]

このように\(\cos\)の式にすることができました。

ここで、\(\cos \theta\)を求める際に符号の正負に気を付けましょう。

今回は\(\theta\)が鋭角なので、\(\cos \theta > 0\)

\[\displaystyle \cos \theta=\frac{2\sqrt{2}}{3}\]

\(\sin \theta\)もしくは\(\cos \theta\)が分かるときは相互関係①を用いることで、もう一方も求めることができます。

\(\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}\)

相互関係①の公式で\(\sin \theta,\cos \theta\)を求めた後に\(\tan \theta\)を求めましょう。

\(\displaystyle \sin \theta=\frac{1}{3}\),\(\displaystyle \cos \theta=\frac{2\sqrt{2}}{3}\)のとき、

\begin{eqnarray}
\displaystyle \tan \theta &=& \frac{\sin \theta}{\cos \theta}\\
\displaystyle &=& \frac{\frac{1}{3}}{\frac{2\sqrt{2}}{3}}\\
\displaystyle &=& \frac{1}{3} × \frac{3}{2\sqrt{2}}\\
\displaystyle &=& \frac{1}{2\sqrt{2}}\\
\displaystyle &=& \frac{\sqrt{2}}{4}
\end{eqnarray}

逆に\(\tan \theta\)と\(\sin \theta\)が分かっていて、\(\cos \theta\)を求めるパターンもあります。

公式を暗記するだけでなく、式を変形して使いこなせるように慣れていきましょう！

\(\displaystyle 1+\tan ^{2} \theta=\frac{1}{\cos ^{2} \theta}\)

この公式は\(\tan \theta\)もしくは\(\cos \theta\)が分かる時に使う公式です。

\(\theta\)が鋭角で、\(\displaystyle \tan \theta=\frac{\sqrt{2}}{4}\)のとき、

\begin{eqnarray}
\displaystyle 1+\tan ^{2} \theta &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle 1+\frac{2}{16} &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle \frac{9}{8} &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle \cos ^{2} \theta &=& \frac{8}{9}
\end{eqnarray}

\(\theta\)が鋭角なので、\(\cos \theta >0\)

\[\displaystyle \cos \theta = \frac{2\sqrt{2}}{3}\]

三角比の相互関係　証明

三角比の相互関係がなぜ成り立つのか、それぞれの式を証明しておきましょう。

証明が必要ない方は、次の「三角関数の相互関係　使い方」へ進んでください。

下の図のような三角形を元に証明していきます。

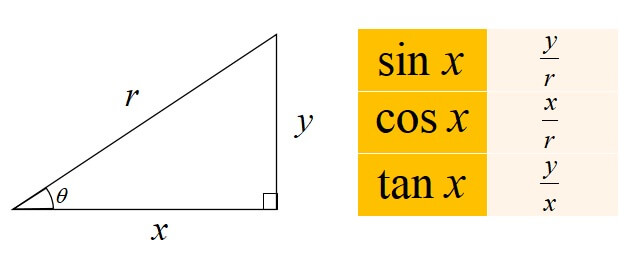
相互関係①\(\sin^{2} \theta+\cos^{2} \theta=1\)

まずは\(\sin^{2} \theta+\cos^{2} \theta=1\)から証明していきます。

これが１番の軸となる公式なので、最優先で\(\sin^{2} \theta+\cos^{2} \theta=1\)を叩き込んでください。

\(\displaystyle \sin \theta=\frac{y}{r}, \cos \theta=\frac{x}{r}\)を変形すると、各辺を下図のように表すことができます。

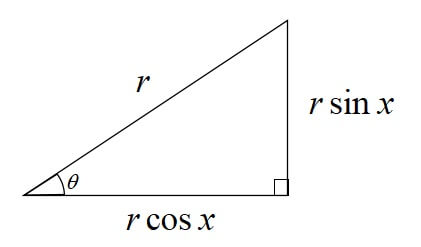
三平方の定理より、

\[r^2=(r \sin \theta)^{2}+(r \cos \theta)^{2}\]

\[r^2=r^{2} \sin^{2} \theta+r^{2} \cos^{2} \theta\]

両辺を\(r^{2}\)で割って、

\[1=\sin^{2} \theta+\cos^{2} \theta\]

よって、\(\sin^{2} \theta+\cos^{2} \theta=1\)の証明終了です。

相互関係②\(\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}\)

相互関係①が理解できた方はすぐにピンときますね。

まず三角比の定義より、

\[\tan \displaystyle \theta=\frac{y}{x}\]

先ほどの三角形の図から分かるように\(y=r \sin \theta,x=r \cos \theta\)なので、

\begin{eqnarray}
\tan \displaystyle \theta &=& \frac{y}{x}\\
&=& \displaystyle \frac{r \sin \theta}{r \cos \theta}\\
&=& \displaystyle \frac{\sin \theta}{\cos \theta}
\end{eqnarray}

よって、\(\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}\)の証明終了です。

相互関係③\(\displaystyle 1+\tan ^{2} \theta=\frac{1}{\cos ^{2} \theta}\)

相互関係①を変形して証明します。

\[\sin^{2} \theta+\cos^{2} \theta=1\]

両辺を\(\cos^{2} \theta\)で割ります

\[\displaystyle \frac{\sin^{2} \theta}{\cos^{2} \theta}+\frac{\cos^{2} \theta}{\cos^{2} \theta}=\frac{1}{\cos^{2} \theta}\]

\[\displaystyle \tan^{2} \theta+1=\frac{1}{\cos^{2} \theta}\]

よって、証明終了です。

三角比の相互関係＜練習問題＞

それでは、今回学んだことを活かして練習問題を解いてみましょう。

解答

\begin{eqnarray}
\sin^{2} \theta+\cos^{2} \theta &=& 1\\
\displaystyle \left( \frac{2}{3} \right)^{2}+\cos^{2} \theta &=& 1\\
\displaystyle \frac{4}{9}+\cos^{2} \theta &=& 1\\
\displaystyle \cos^{2} \theta &=& \frac{5}{9}\\
\displaystyle \cos \theta &=& ±\sqrt{\frac{5}{9}}\\
\displaystyle &=& ±\frac{\sqrt{5}}{3}
\end{eqnarray}

\(\theta\)が鋭角なので、\(\cos \theta>0\)なので、

\[\displaystyle \cos \theta=\frac{\sqrt{5}}{3}\]

これで\(\sin \theta\)と\(\cos \theta\)が分かったので、相互関係②の公式に代入しましょう。

\begin{eqnarray}
\displaystyle \tan \theta &=& \frac{\sin \theta}{\cos \theta}\\
\displaystyle &=& \frac{\frac{2}{3}}{\frac{\sqrt{5}}{3}}\\
\displaystyle &=&\frac{2}{3} × \frac{3}{\sqrt{5}}\\
\displaystyle &=&\frac{2}{\sqrt{5}}
\end{eqnarray}

有理化して、

\[\displaystyle \tan \theta=\frac{2\sqrt{5}}{5}\]

解答

\begin{eqnarray}
\displaystyle 1+\tan ^{2} \theta &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle 1+(\frac{1}{2})^{2} &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle 1+\frac{1}{4} &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle \frac{5}{4} &=& \frac{1}{\cos ^{2} \theta}\\
\displaystyle \cos ^{2} \theta &=& \frac{4}{5}\\
\displaystyle \cos \theta &=& ±\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}
\end{eqnarray}

\(\theta\)は鋭角なので、

\[\displaystyle \cos \theta=\frac{2\sqrt{5}}{5}\]

\begin{eqnarray}
\sin^{2} \theta+\cos^{2} \theta &=&1\\
\displaystyle \sin^{2} \theta+\left(\frac{2\sqrt{5}}{5} \right)^{2}&=&1\\
\displaystyle \sin^{2} \theta+\frac{20}{25}&=&1\\
\displaystyle \sin^{2} \theta &=& \frac{5}{25}
\end{eqnarray}

\(\theta\)は鋭角なので、

\[\displaystyle \sin \theta=\frac{\sqrt{5}}{5}\]

三角比の相互関係　まとめ

今回は必ず覚えたい重要公式の1つ“三角比の相互関係”を解説しました。

繰り返しになりますが、三角比の相互関係は当たり前に使えるようにしましょう。

これから習う数Ⅱ「三角関数」でも三角比の式変形は必須です。

三角比には覚えておきたい重要公式がたくさんあるので、以下の記事もぜひ参考にしてください。

三角比を一気に復習したい方はこちらの記事がおすすめです。

それでは最後まで見ていただいてありがとうございました。

みんなの努力が報われますように！