『2次関数』は数学Ⅰにおける重要な単元の1つです。
共通テストや大学入試でも二次関数はよく出題される単元なので、文系・理系に関わらず確実に理解しましょう!
2次関数の公式まとめ
まずは2次関数において確実に押さえたい“重要な公式6つ”をリストアップしました。
2次関数の公式を大急ぎで知りたい方はこちらをご覧ください。
2次関数の基本公式
\(a≠0\)において、下記のような式を2次関数といいます。
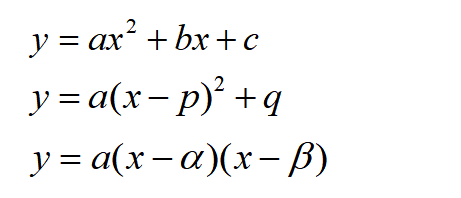
ベーシックな形は1番上の式ですが、上記はどれも2次関数を表しています。
2,3番目の式も展開すると1番上のような形になるので、心配な人はぜひ展開してみてください。
上記の2次関数の式はどれも2次関数の決定で使うので、どの形も思い出せるようにしておきましょう。
グラフの軸と頂点
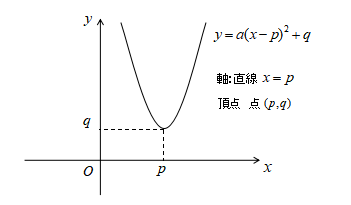
2次関数のグラフの形が分かる公式です。
2次関数 \(y=a(x-p)^{2}+q\) において、
放物線の軸:\(x=p\)
頂点の座標:\((p,q)\)
グラフの平行移動
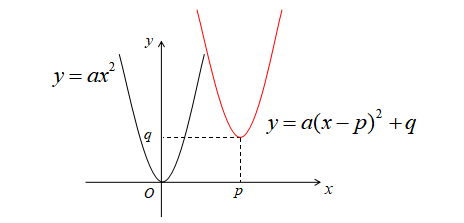
2次関数を平行移動させる問題はこの公式で解決できます。
\(y=ax^{2}\) のグラフを \(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\[y=a(x-p)^{2}+q\]
2次関数の決定
2次関数の決定は大きく3つの型に分けられます。

問題文で与えられた条件から上記のどの型を使うのか判断し、2次関数を求めます。
- 問題文で「頂点の座標」もしくは「軸のx座標」が与えられている
- \(y=a(x-p)^{2}+q\)
- 問題文で3点の座標が与えられている
- \(y=a^{2}+bx+c\)
- 問題文でx軸との交点が2つ与えられている
- \(y=a(x-p)(x-q)\)
2次関数の解の公式
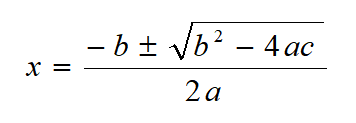
2次方程式 \(ax^{2}+bx+c=0\)\((a≠0)\) において、解の公式を使うと方程式の解を求めることができます。
判別式Dを求める公式
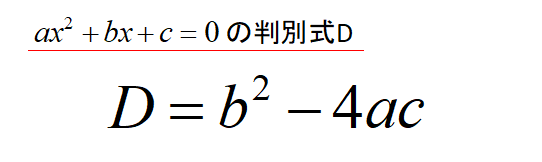
判別式Dの符号によって、2次方程式の実数解がいくつあるのかを求めることができます。
2次方程式 \(ax^{2}+bx+c=0\) の判別式
\[D=b^{2}-4ac\]
上で紹介した公式はどれも2次関数に欠かせない重要な公式です。
2次関数とは次数2の関数
2次関数を一言で言うと、「変数の次数(右肩に乗っている数字)が最大で2である関数」のことです。
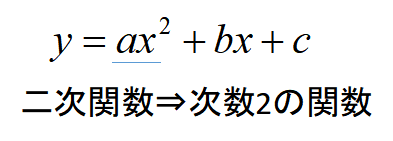
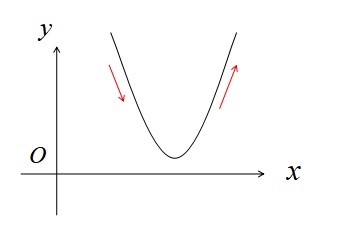
1次関数のグラフが直線だったのに対して、2次関数のグラフは放物線という滑らかな曲線を描きます。
そもそも関数とは?
(x)の値を1つ決めたとき、それに伴って(y)の値も1つに決まる数式のこと。
1次関数 \(y=2x , y=-3x+2\)
2次関数 \(y=3x^{2}+2x+1\)
3次関数 \(y=ax^{3}+bx^{2}+cx+d\)
4次関数 \(y=ax^{4}+bx^{3}+cx^{2}+dx+e\)
2次関数の頂点と軸
2次関数のグラフ(放物線)において、「頂点」と「軸」はグラフの場所や形を決定する最も重要な要素です。
自分で平方完成をして \(y=a(x-p)^{2}+q\) の形にして、軸と頂点を求める問題もあります。

2次関数 \(y=a(x-p)^{2}+q\) において、
放物線の軸:\(x=p\)
頂点の座標:\((p,q)\)
平方完成を使って2次関数の頂点・軸を求める手順については別ページで解説しています。
平方完成して頂点と軸を求める
自分で平方完成する場合は以下の手順で進めてください。
2次関数が以下の形になれば軸と頂点が分かります。
\[y=a(x-p)^{2}+q\]
【補足】平方完成とは?
\(ax^{2}+bx+c\) の形の2次式を \(a(x−p)^{2}+q\) の形へ変形することを平方完成と言います。
2次関数 \(x^{2}+6x+5\) を例として、軸と頂点を求めてみましょう。
\begin{eqnarray}
x^{2}+6x+5&=&(x^{2}+6x+9)-9+5\\
&=&(x+3)^{2}-4
\end{eqnarray}
与式を\((x+3)^{2}-4\)に変形できたので、グラフの軸と頂点を読み取ることができます。
放物線の軸:\(x=-3\)
頂点の座標:\((-3,-4)\)
このように平方完成を用いて、2次関数のグラフの頂点と軸を求められるようになりましょう。
2次関数のグラフの書き方
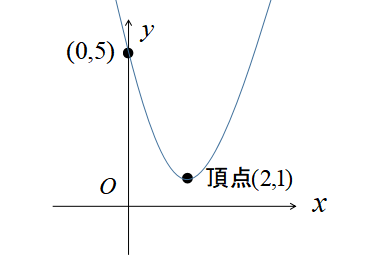
2次関数のグラフは以下の3ステップで書くことができます。
Step1:頂点を求める
Step2:y軸との交点を求める
Step3:頂点とy軸との交点を滑らかにつなぐ
\(y=x^{2}+6x+5\)を例にしてグラフを書いてみましょう。
初めに2次関数のグラフの頂点を求めましょう。
頂点の座標は、2次関数の式を平方完成することで求められます。
例として、\(y=x^{2}+6x+5\)を平方完成すると
\begin{eqnarray}
y&=&x^{2}+6x+5\\
&=&(x+3)^{2}-4
\end{eqnarray}
となります。
したがって、\(y=x^{2}+6x+5\)の頂点は \(-3,-4\) となります。

頂点の座標が分かっただけではグラフは書けません。
次はグラフとy軸との交点を求めます。
y軸上の点ということは、x座標が0であるので式に \(x=0\) を代入します。
\(y=x^{2}+6x+5\)に\(x=0\)を代入すると
\begin{eqnarray}
y&=&0^{2}+6 \cdot 0+5\\
&=&5
\end{eqnarray}
したがって、\(y=x^{2}+6x+5\) のグラフは\((0,5)\)でy軸と交わることが分かりました。
最後に頂点とy軸との交点を滑らかにつなぎます。
\(y=x^{2}+6x+5\)の頂点は\((-3,-4)\)、y軸との交点は\((0,5)\)でした。
この2点を滑らかにつなぎ、左右対称に描くと2次関数のグラフが完成します。
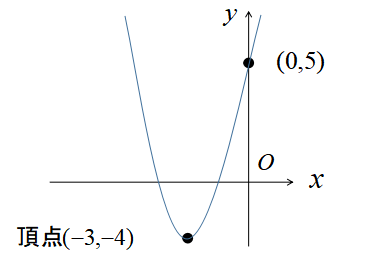
上記の3ステップを丁寧に進めれば、誰でも2次関数のグラフが書けます。
Step1:頂点を求める
Step2:y軸との交点を求める
Step3:頂点とy軸との交点を滑らかにつなぐ
2次関数の平行移動
グラフの形を変えないまま、平行に移動させることを平行移動といいます。
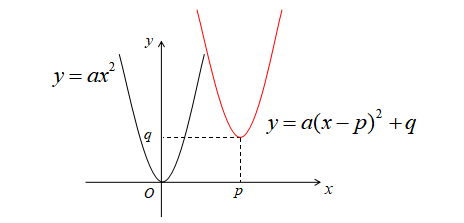
このとき、放物線の形は変わりませんが、頂点や軸の位置が移動しているため、2次関数の式は変わります。
\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させると
\[y=a(x-p)^{2}+q\]
\(y=x^{2}\)を\(x\)軸方向に\(3,y\)軸方向に\(2\)だけ平行移動させると、\(y=(x-3)^{2}+2\)となります。
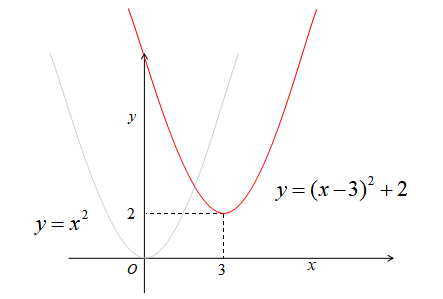
2次関数\(y=x^{2}+6x+4\)を、\(x\)軸方向に\(-2,y\)軸方向に\(3\)だけ平行移動させます。
このとき、\(y=x^{2}+6x+4\)を平行移動させる方法は2つあります。
- そのまま平行移動
- 平方完成してから平行移動
方法1.そのまま平行移動
\(y=x^{2}+6x+4\)を\(x\)軸方向に\(-2,y\)軸方向に\(3\)だけ平行移動するので、
\begin{eqnarray}
y&=&(x+2)^{2}+6(x+2)+4+3\\
&=&(x^{2}+4x+4)+6(x+2)+7\\
&=&x^{2}+10x+23
\end{eqnarray}
したがって、求める2次関数は\(y=x^{2}+10x+23\)だと分かりました。
方法2.平方完成してから平行移動
平方完成してから平行移動する方法も紹介します。
まずは\(y=x^{2}+6x+4\)を平方完成します。
\begin{eqnarray}
y&=&x^{2}+6x+4\\
&=&(x+3)^{2}-9+4\\
&=&(x+3)^{2}-5
\end{eqnarray}
この関数が\(x\)軸方向に\(-2\),\(y\)軸方向に\(3\)だけ平行移動するので
\begin{eqnarray}
y&=&(x+3+2)^{2}-5+3\\
&=&(x+5)^{2}-2\\
&=&x^{2}+10x+23
\end{eqnarray}
したがって、求める2次関数は\(y=x^{2}+10x+23\)となりました。
2次関数のグラフを平行移動させる公式は別記事で解説しているので、スムーズに移動させられるようにしておきましょう。
2次関数の最大値・最小値
2次関数では、最大値・最小値を求める問題もよく出題されます。
2次関数の最大値と最小値の問題は大きく4つのタイプがあります。
- 定義域がない場合
- 定義域がある場合
- 定義域に文字を含む場合
- 軸に文字を含む場合
最大値・最小値の求め方は問題のパターンによって異なります。
ここではざっくりとした解説をします。詳しく知りたい方は「2次関数の最大値・最小値を求める4つのパターン」をご覧ください。
定義域がない場合
定義域(範囲)のないパターンの問題から解説します。
定義域がない場合というのは以下のような問題です。
次の2次関数に最大値、最小値があれば求めなさい。
\(y=x^{2}-4x+3\)
\(y=-2x^{2}-4x\)
\(y=x^{2}-4x+3\)の最大値・最小値
まずは関数を変形して、グラフの軸と頂点を求めます。
\begin{eqnarray}
y&=&x^{2}-4x+3\\
&=&(x-2)^{2}-1
\end{eqnarray}
この関数をグラフにすると下図のようになります。
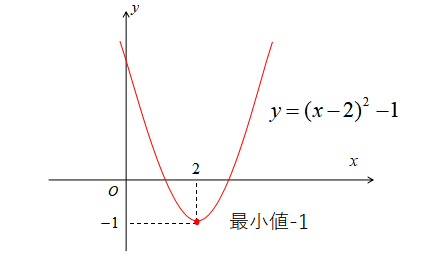
よって、この2次関数は\(x=2\)で最小値\(-1\)をとります。
また、グラフは永遠に上方向に伸びていくため、この問題において最大値は存在しません。
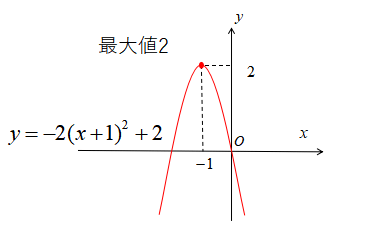
\(y=-2x^{2}-4x\)の最大値・最小値
関数の式を変形すると
\begin{eqnarray}
y&=&-2x^{2}-4x\\
&=&-2(x+1)^{2}+2
\end{eqnarray}
この関数をグラフにすると下図のようになります。

よって、この2次関数は\(x=-1\)で最大値\(2\)をとります。
また、グラフは永遠に下方向に伸びていくので最小値はありません。
上の2問のようにグラフに定義域が与えられていないときは、グラフが最大値、最小値を持たない場合もあるので注意して下さい。
定義域がある場合
定義域がある場合は、以下ような問題が出題されます。
次の2次関数の最大値、最小値を求めなさい。
\(y=x^{2}-4x+1 (0≦x≦3)\)
\(y=-2x^{2}+4x+5 (-1≦x≦0)\)
\(y=x^{2}-4x+1 (0≦x≦3)\)の最大値・最小値
まずは関数を変形して、
\begin{eqnarray}
y&=&x^{2}-4x+1\\
&=&(x-2)^{2}-3
\end{eqnarray}
ここで\(0≦x≦3\)なので、グラフは下図の実践部分になります。
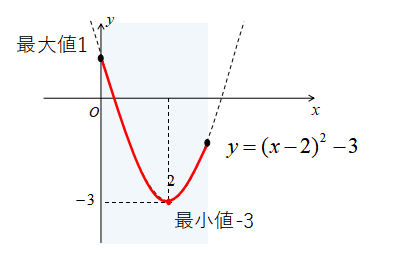
このグラフの実践部分で最大なのは\(x=0\)のときの\(y=1\)
また、実践部分で最小なのが\(x=2\)のときの\(y=-3\)です。
\(x=0\)のとき、最大値\(-1\)
\(x=2\)のとき、最小値\(-3\)
\(y=-2x^{2}+4x+3 (-1≦x≦0)\)の最大値・最小値
まずは関数を変形して、
\begin{eqnarray}
y&=&-2x^{2}+4x+3\\
&=&-2(x-1)^{2}+5
\end{eqnarray}
ここで\(-1≦x≦0\)なので、グラフは下図の実践部分になります。
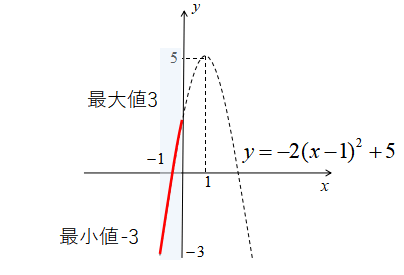
このグラフの実践部分で最大なのは\(x=0\)のときの\(y=3\)
また、実践部分で最小なのが\(x=-1\)のときの\(y=-3\)です。
\(x=0\)のとき、最大値\(3\)
\(x=-1\)のとき、最小値\(-3\)
定義域に文字を含む場合
定義域に文字を含むというのは、以下のような問題のことです。
次の2次関数の最大値、最小値を求めなさい。
\(y=x^{2}-2x+3 (0≦x≦a)\)
一つ前の定義域がある場合と同じように見えますが、よく見ると範囲に文字が含まれています。
この場合、\(a\)の値によって範囲が変化するため場合分けが必要です。
まずは関数を変形します。
\begin{eqnarray}
y&=&x^{2}-2x+3\\
&=&(x-1)^{2}+2
\end{eqnarray}
この問題では\(x\)の定義域が\(0≦x≦a\)でした。
ここで\(a\)の値によって、以下の4つの場合分けします。
- \(a<1\)のとき
- \(1≦a<2\)のとき
- \(a=2\)のとき
- \(2<a\)のとき
\(a<1\)のとき
\(a<1\)のとき、定義域に含まれるグラフは下図のようになります。
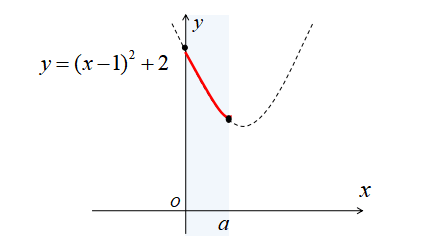
\(a<1\)のとき、\(y=(x-1)^{2}+2\)の軸は定義域に含まれていません。
したがって、\(a<1\)のときの最大値、最小値は
\(x=0\)のとき、最大値\(3\)
\(x=a\)のとき、最小値\(a^{2}-2a+3\)
\(1≦a<2\)のとき
\(1≦a<2\)のとき、定義域に含まれるグラフは下図のようになります。
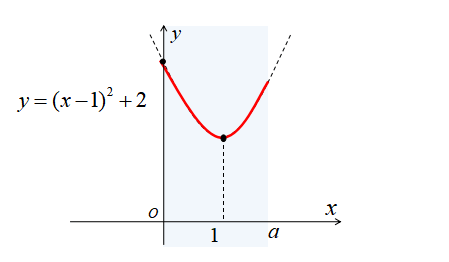
\(1≦a<2\)のとき、\(y=(x-1)^{2}+2\)の軸が定義域に含まれています。なので頂点が最小値になることが図から分かります。
したがって、\(1≦a<2\)のときの最大値、最小値は
\(x=0\)のとき、最大値\(3\)
\(x=1\)のとき、最小値\(2\)
\(a=2\)のとき
\(a=2\)のとき、定義域に含まれるグラフは下図のようになります。
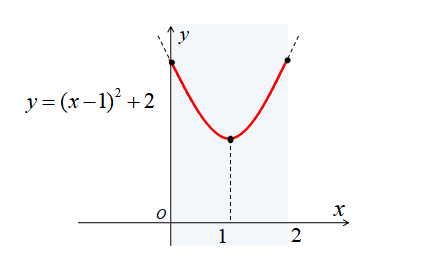
\(a=2\)のとき、図から分かるように最大値をとる点が2つ存在します。
したがって、\(a=2\)のときの最大値、最小値は
\(x=0,2\)のとき、最大値\(3\)
\(x=1\)のとき、最小値\(2\)
\(2<a\)のとき
\(2<a\)のとき、定義域に含まれるグラフは下図のようになります。
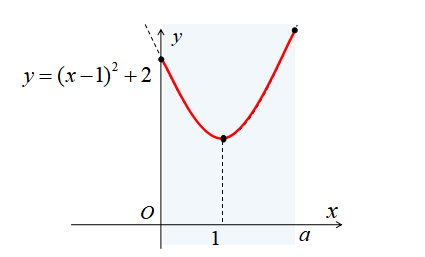
\(2<a\)のとき、定義域の右端が最大値をとるようになります。
したがって、\(2<a\)のときの最大値、最小値は
\(x=a\)のとき、最大値\(a^{2}-2a+3\)
\(x=1\)のとき、最小値\(2\)
したがって、求める最大値、最小値は
解答
\(a≦1\)のとき、最大値3、最小値\(\a^{2}-2a+3\)
\(1≦a≦2\)のとき、最大値3、最小値2
\(2≦a\)のとき、最大値\(a^{2}-2a+3\)、最小値2
軸に文字を含む場合
最後は軸に文字を含む場合ですが、以下のような問題が出題されます。
\(a\)は定数とします。
2次関数\(y=2x^{2}-4ax (0≦x≦1)\)の最小値を、それぞれの場合で求めましょう。
(1) \(a<0\)
(2) \(0≦a≦1\)
(3) \(1<a\)
まずは関数を変形します。
\begin{eqnarray}
y&=&2x^{2}-4ax\\
&=&2(x^{2}-2ax)\\
&=&2(x-a)^{2}-2a^{2}
\end{eqnarray}
ここで\(a\)の値によって、以下の3問を解いてみましょう。
(1) \(a<0\)
(2) \(0≦a≦1\)
(3) \(1<a\)
\(a<0\)の場合
\(a<0\)のとき、グラフは下図のようになります。
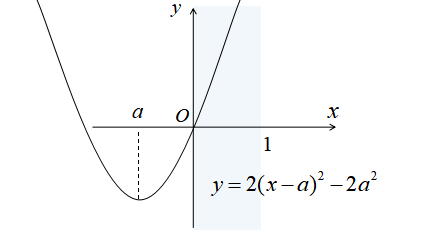
\(a<0\)のとき、\(x=0\)で最小値0をとります。
\(0≦a≦1\)の場合
\(0≦a≦1\)のとき、グラフは下図のようになります。
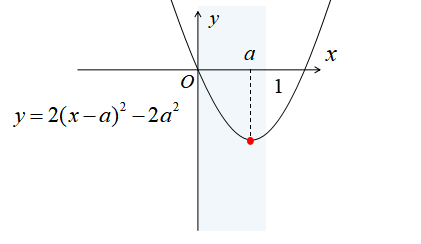
したがって\(0≦a≦1\)のとき、\(x=a\)で最小値\(-2a^{2}\)をとります。
\(1<a\)の場合
\(1<a\)のとき、グラフは下図のようになります。
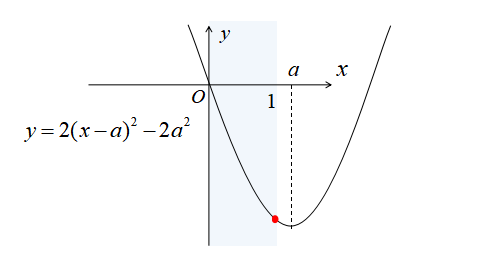
\(1<a\)のとき、\(x=1\)で最小値\(2-4a\)となる。
解答
\(a<0\)のとき、最小値0
\(0≦a≦1\)のとき、最小値\(-2a^{2}\)
\(1<a\)のとき、最小値\(2-4a\)
2次関数の最大値・最小値の問題はかなりの確率で定期テストに出題されます。
2次関数の決定
2次関数の決定は大きく3つのパターンに分けられます。

問題文で与えられたヒントからどのパターンなのかを考えます。
①頂点と1点の座標が分かっているとき
頂点の座標と他の1点が分かっているときは①のパターンです。

次の条件を満たす2次関数を求めよう。
頂点が点\((2,-4)\)で,点\((-1,5)\)を通る。
頂点の座標から求める2次関数が以下の形をしていることが分かります。
\[y=a(x-2)^{2}-4\]
この2次関数が点\((-1,5)\)を通るので、\(x=-1,y=5\)を代入して
\begin{eqnarray}
5&=&a(-1-2)^{2}-4\\
5&=&9a-4\\
a=1
\end{eqnarray}
よって、\(\displaystyle a=1\)を式に代入して、
求める2次関数の式は \(\displaystyle y=(x-2)^{2}-4\)だと分かりました。
②軸と2点の座標
軸の直線と他の2点の座標が分かっているときも①のパターンです。
次の条件を満たす2次関数を求めよう。
直線\(x=3\)を軸として、2点\((-1,4),(1,-8)\)を通る。
軸が\(x=3\)なので、
\(y=a(x-3)^{2}+q\)
この2次関数が
点(-1,4)を通るから、\(4=a(-1-3)^{2}+q\)
点(1,-8)を通るので、\(-8=a(1-3)^{2}+q\)
よって、
\begin{eqnarray}
4&=&16a+q \cdots ①\\
-8&=&4a+q \cdots ②
\end{eqnarray}
これを連立方程式で解くと \(a=1,q=-12\)
よって、求めたい2次関数が\(y=(x-3)^{2}-12\)だと分かりました。
③3点の座標
通る点の座標が3つ分かっているときは②のパターンです。

3点\((2,-2),(3,5),(-1,1)\)を通る2次関数の式を求めなさい。
3点が分かっているときは連立方程式を使います。
この2次関数が
点(2,-2)を通るから、\(-2=4a+2b+c \cdots ①\)
点(3,5)を通るので、\(5=9a+3b+c \cdots ②\)
点(-1,1)を通るので、\(1=a-b+c \cdots ③\)
②-①から、\(7=5a+b \cdots ④\)
②-③から、\(4=8a+4b \cdots ⑤\)
④×4-⑤から、\(24=12a\)となり\(a=2\)
④に\(a=2\)を代入すると、\(b=-3\)
①に\(a=2,b=-3\)を代入すると、\(c=-4\)
したがって、求める2次関数は\(y=2x^{2}-3x-4\)だと分かりました。
④x軸との交点と1点の座標
x軸との交点が2点と他の1点の座標が分かっているときは③のパターンです。

x軸と点\((1,0),(3,0)\)と交わり、点\((-1,8)\)を通る2次関数を求めよう。
x軸と点(1,0),(3,0)で交わるので、2次関数が以下の形をしていることが分かります。
\(y=a(x-1)(x-3)\)
この2次関数が点(-1,8)を通るので、
\begin{eqnarray}
8&=&a(-1-2)(-1-3)\\
8&=&12a\\
\displaystyle a&=&\frac{2}{3}
\end{eqnarray}
よって、求めたい2次関数が\(\displaystyle y=\frac{2}{3}(x-1)(x-3)\)だと分かりました。
説明が長くなってしまいましたが、2次関数の決定は慣れれば点数が取れる単元なので、沢山練習しましょう。
2次方程式と解の公式
2次方程式の解の求め方は主に2つあります。
- 因数分解して求める
- 解の公式を用いて求める
因数分解で解を求める
解の公式を解説する前に因数分解で求める方法を紹介します。
必ず押さえて欲しいので確認しておきましょう。
\begin{eqnarray}
x^{2}-5x+4&=&0\\
(x-1)(x-4)&=&0
\end{eqnarray}
したがって、\(x=1,4\)
\begin{eqnarray}
2x^{2}-4x-6&=&0\\
2(x^{2}-2x-3)&=&0\\
2(x+1)(x-3)&=&0
\end{eqnarray}
したがって、\(x=-1,3\)
解の公式を用いて求める
2次方程式\(ax^{2}+bx+c=0\)の解は以下の計算で求めることができます。
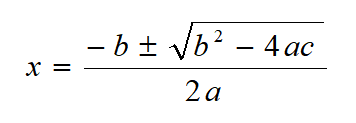
解の公式はかなり便利な公式なので必ず覚えましょう。
解の公式ならキレイに因数分解ができない2次方程式も解を求められます。
\(x^{2}-4x+1=0\)
\(a=1,b=-4,c=1\)として、解の公式に代入します。
\begin{eqnarray}
D&=&\frac{-b±\sqrt{b^{2}-4ac}}{2a}\\
&=&\frac{-(-4)±\sqrt{(-4)^{2}-4 \cdot 1 \cdot 1}}{2 \cdot 1}\\
&=&\frac{4±\sqrt{16-4}}{2}\\
&=&\frac{4±2\sqrt{3}}{2}\\
&=&2±\sqrt{3}
\end{eqnarray}
したがって、\(x=-2±\sqrt{6}\)となります。
解の公式は必ず押さえておきたい公式です。
2次方程式の判別式D
2次方程式\(ax^{2}+bx+c=0\)において、以下の公式を判別式といいます。
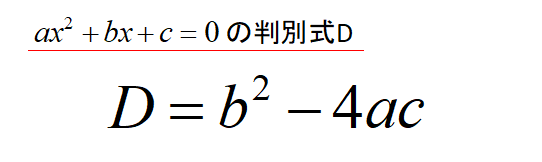
判別式の符号によってさまざまなことが分かるのでそれを解説していきましょう。
方程式の解の個数
判別式Dの符号によって、方程式を満たす実数解の個数が分かります。

例として、1つ問題を解いてみましょう。
例題1
次の2次方程式の実数解の個数を求めよう。
\(x^{2}+3x-5=0\)
\(a=1,b=3,c=-5\)として判別式Dに代入します。
\begin{eqnarray}
D&=&b^{2}-4ac\\
&=&3^{2}-4 \cdot 1 \cdot (-5)\\
&=&9+20\\
&=&29
\end{eqnarray}
D>0なので、異なる2つの実数解をもつ。
x軸との共有点の個数
判別式Dの符号によって、2次関数とx軸との共有点の個数も分かります。
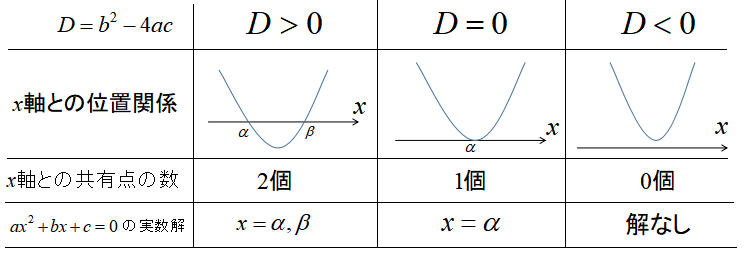
【補足】実数解の個数って、何の個数を表しているの?
\(ax^{2}+bx+c=0\)の実数解は、2次関数\(y=ax^{2}+bx+c\)とx軸との共有点のx座標を表しています。
これも例題で慣れていきましょう。
例題2
次の2次関数のグラフとx軸の共有点の個数を求めよう。
(1) \(y=x^{2}+3x+2\)
(2) \(y=2x^{2}-3x+2\)
(1) 2次方程式\(x^{2}+3x+2=0\)の判別式をDとすると
\begin{eqnarray}
D&=&b^{2}-4ac\\
&=&3^{2}-4 \cdot 1 \cdot 2\\
&=&9-8\\
&=&1
\end{eqnarray}
D>0より、グラフとx軸の共有点の個数は2個である。
(2) 2次方程式\(2x^{2}-3x+2=0\)の判別式をDとすると
\begin{eqnarray}
D&=&b^{2}-4ac\\
&=&(-3)^{2}-4 \cdot 2 \cdot 2\\
&=&9-16\\
&=&-7
\end{eqnarray}
D<0より、グラフはx軸の共有点をもたない。
このように共有点を持たない場合もあるから注意が必要です。
判別式Dと解の個数については別の記事でも詳しく解説しています。
2次関数《練習問題》
2次関数の練習問題をいくつか用意しました。
実際にノートに計算していただいても良いですし、今回は解法の確認に活用してもOKです!
練習問題1
次の2次関数の軸と頂点を求めよう。
\(y=x^{2}-4x+3\)
軸と頂点を求めるには、\(y=a(x-p)^{2}+q\)の形に式変形します。
\begin{eqnarray}
y&=&x^{2}-4x+3\\
&=&(x-2)^{2}-1
\end{eqnarray}
したがって、求める軸と頂点が分かりました。
◇解答
軸の直線:\(x=2\)
頂点の座標:\((2,-1)\)
練習問題2
次の2次関数の最大値、最小値を求めよう。
\(y=x^{2}+2x+3 (-2≦x≦2)\)
まずは関数を変形します。
\begin{eqnarray}
y&=&x^{2}+2x+3\\
&=&(x+1)^{2}+2
\end{eqnarray}
ここで\(-2≦x≦2\)なので、グラフは下図の実践部分になります。
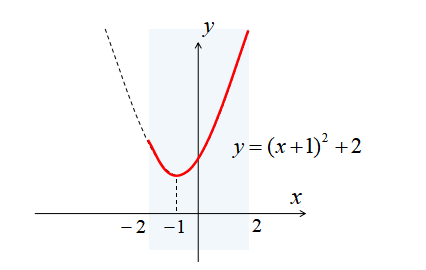
このグラフの実践部分は\(x=2\)のとき最大値\(11\)をとります。
また、頂点が定義域に含まれているので\(x=-1\)のとき最小値2となります。
したがって、求める最大値、最小値は
\(x=2\)のとき、最大値11
\(x=-1\)のとき、最小値2
練習問題3
2次方程式 \(x^{2}-2x+m=0\) が異なる2つの実数解をもつとき、定数\(m\)の値の範囲を求めなさい。
この2次方程式の判別式をDとすると
\begin{eqnarray}
D&=&b^{2}-4ac\\
&=&(-2)^{2}-4 \cdot 1 \cdot m\\
&=&4-4m
\end{eqnarray}
2次方程式が異なる2つの実数解をもつのは、\(D>0\)のときなので
\begin{eqnarray}
4-4m&>&0\\
m&<&1
\end{eqnarray}
したがって、\(m<1\)のとき異なる2つの実数解をもつ。
2次関数の公式【まとめ】
今回は2次関数を総復習できるように網羅的にまとめました。
2次関数の形を覚えておこう
- \(y=ax^{2}+bx+c\)
- \(y=a(x-p)^{2}+q\)
- \(y=a(x-\alpha)(x-\beta)\)

グラフの軸と頂点が読み取れるようにしよう
2次方程式 \(y=a(x-p)^{2}+q\) において、
軸の直線:\(x=p\) 、頂点の座標:\((p,q)\)
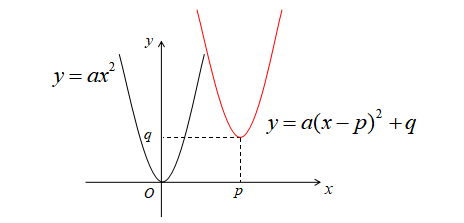
2次関数の平行移動は式で表す
\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\(y=a(x-p)^{2}+q\)
2次関数の決定は3つの型に分けられる。

判別式Dの符号によって、実数解の個数が分かる
- D>0 ⇒ 異なる2つの実数解をもつ
- D=0 ⇒ 実数解を1つもつ(重解)
- D<0 ⇒ 実数解をもたない
2次関数は問題のバリエーションが豊富なので、苦手意識を持っている人も多いです。
しかし問題の意図を正しく捉えられれば、ここで紹介した公式だけでほとんどの問題を解くことができます。
2次関数以外の単元についてもまとめ記事を出しています。
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

