[mathjax]
数学Ⅰ二次関数の中でも「二次関数の最大値・最小値」を求める問題は難しいですよね。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”50px auto 40px”]
「2次関数の最大値・最小値ってどうやって求めるの?」
「最大値・最小値の問題が苦手で…」
[/st-mybox]
今回は2次関数の中でも「最大値・最小値」に関する悩みを解決します。
 シータ
シータ最大値・最小値の問題には大きく4つのタイプがあるよ
「最大値・最小値を求める問題は難しい…」
そんな風に感じている方も多いと思います。
しかし安心してください!
実は、最大値・最小値の問題は大きく4つのパターンしかありません。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 範囲がない場合
- 範囲がある場合
- 範囲に文字を含む場合
- 軸に文字を含む場合
※詳細は下の目次からジャンプしてね!
[/st-mybox]
本記事では、2次関数の最大値・最小値の解き方をタイプ別に解説します。
自分の苦手な問題タイプの問題を探して、ぜひ解き方を学んでいってください。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
《復習》2次関数のグラフの書き方
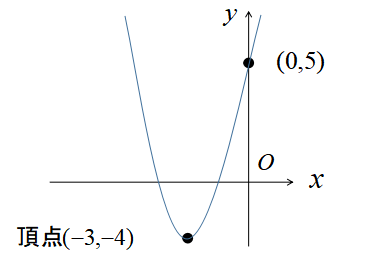
2次関数のグラフは以下の手順で書くことができます。
[st-mybox title=”グラフを書く手順” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”3″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 軸・頂点を求める
- y軸との交点を求める
- 頂点とy軸に交点を滑らかに結ぶ
[/st-mybox]
2次関数のグラフの書き方を詳しく知りたい方はこちらの記事からご覧ください。
⇒2次関数のグラフの書き方を3ステップで解説!
 シータ
シータグラフが書けないと最大値・最小値がイメージできないよ
2次関数の最大値・最小値

2次関数の最大値と最小値の求め方を解説します。
最大値と最小値の問題は大きく分けて4つのタイプがあります。
[st-mybox title=”最大値・最小値の4つのタイプ” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 範囲がない場合
- 範囲がある場合
- 範囲に文字を含む場合
- 軸に文字を含む場合
[/st-mybox]
それぞれのパターンで最大値・最小値の求め方が異なるので、1つずつ読んでみてください。
範囲がない場合
まずは範囲(定義域)のない2次関数の最大値・最小値から解説します。
範囲がない場合というのは以下のような問題です。
[st-mybox title=”範囲がない場合” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の2次関数に最大値、最小値があれば求めよう。
\(y=x^{2}-4x+3\)
\(y=-2x^{2}-4x\)
[/st-mybox]
 高校生
高校生見たことあるけど解けませんでした…
 シータ
シータこれは基本問題なので必ず解けるようにしよう!
\(y=x^{2}-4x+3\)の最大値・最小値
まずは平方完成をしてグラフの軸と頂点を求めます。
\begin{eqnarray}
y&=&x^{2}-4x+3\\
&=&(x-2)^{2}-1
\end{eqnarray}
この関数はグラフにすると下図のようになります。
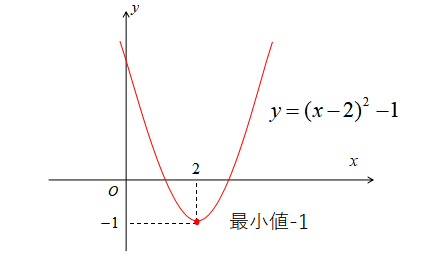
よって、\(y\)は\(x=2\)で最小値-1をとります。
このグラフはずっと上方向に伸びてしまうので最大値はありません。
このように定義域も文字も含まないパターンは、2次関数のグラフが書ければ簡単に最大値・最小値が求められます。
\(y=-2x^{2}-4x\)の最大値・最小値
問題2も考えていきましょう。
関数の式を変形すると
\begin{eqnarray}
y&=&-2x^{2}-4x\\
&=&-2(x+1)^{2}+2
\end{eqnarray}
この関数はグラフにすると下図のようになります。
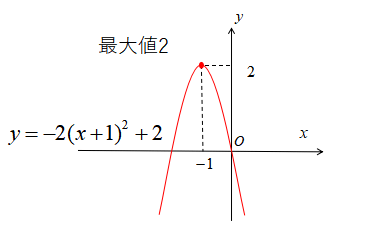
よって、\(y\)は\(x=-1\)で最大値2をとり、グラフは永遠に下方向に伸びていくので最小値はありません。
以上の2問のように定義域がない場合は、“グラフが最大値・最小値を持たない”こともあるので注意して下さい。
 高校生
高校生最大値や最小値がないこともあるんですね
範囲がある場合
次は定義域が与えられている場合を考えてみましょう。
[st-mybox title=”範囲がある場合” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=x^{2}-4x+1 (0≦x≦3)\)
\(y=-2x^{2}+4x+3 (-1≦x≦0)\)
[/st-mybox]
では、この2問を解説します。
\(y=x^{2}-4x+1 (0≦x≦3)\)の最大値・最小値
まずは関数を変形して、
\begin{eqnarray}
y&=&x^{2}-4x+1\\
&=&(x-2)^{2}-3
\end{eqnarray}
ここで\(0≦x≦3\)なので、グラフは下図の実践部分になります。
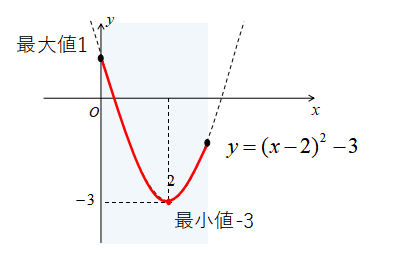
このグラフの実践部分で最大なのは\(x=0\)のときの\(y=1\)
また、実践部分で最小なのが\(x=2\)のときの\(y=-3\)です。
したがって、
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0\)のとき、最大値-1()
\(x=2\)のとき、最小値-3
[/st-mybox]
\(y=-2x^{2}+4x+3 (-1≦x≦0)\)の最大値・最小値
まずは関数を変形して、
\begin{eqnarray}
y&=&-2x^{2}+4x+3\\
&=&-2(x-1)^{2}+5
\end{eqnarray}
ここで\(-1≦x≦0\)なので、グラフは下図の実践部分になります。
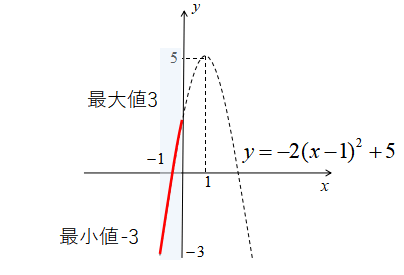
このグラフの実践部分で最大なのは\(x=0\)のときの\(y=3\)
また、実践部分で最小なのが\(x=-1\)のときの\(y=-3\)です。
したがって、
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0\)のとき、最大値3
\(x=-1\)のとき、最小値-3
[/st-mybox]
定義域が定まっている場合も、2次関数のグラフを書くことができれば簡単に最大値・最小値を求めることができます。
範囲に文字を含む場合
範囲(定義域)に文字を含むというのは、以下のような問題のことです。
[st-mybox title=”範囲に文字を含む場合” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=x^{2}-2x+3 (0≦x≦a)\)
[/st-mybox]
見たところ範囲がある場合と同じに見えますが、よく見ると範囲に文字が含まれています。
この場合、\(a\)の値によって範囲が変化するため場合分けが必要です。
 高校生
高校生場合分け苦手だ、、できるかな
 シータ
シータ大丈夫だよ!図使って丁寧に解説するからじっくり読んで見て!
まずは関数を変形します。
\begin{eqnarray}
y&=&x^{2}-2x+3\\
&=&(x-1)^{2}+2
\end{eqnarray}
この問題では\(x\)の定義域が\(0≦x≦a\)でした。
ここで\(a\)の値を以下の4つに場合分けします。
[st-mybox title=”4つの場合分け” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- \(a<1\)のとき
- \(1≦a<2\)のとき
- \(a=2\)のとき
- \(2<a\)のとき
[/st-mybox]
ここからかなり複雑になります。
難しそうに見えますが、落ち着いて読めばきっと理解できるので、ゆっくり読んでみて下さい。
\(a<1\)のとき
\(a<1\)のとき、定義域に含まれるグラフは下図のようになります。
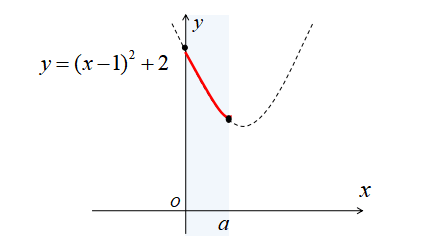
\(a<1\)のとき、\(y=(x-1)^{2}+2\)の軸は定義域に含まれていません。
したがって、\(a<1\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0\)のとき、最大値3
\(x=a\)のとき、最小値\(a^{2}-2a+3\)
[/st-mybox]
\(1≦a<2\)のとき
\(1≦a<2\)のとき、定義域に含まれるグラフは下図のようになります。
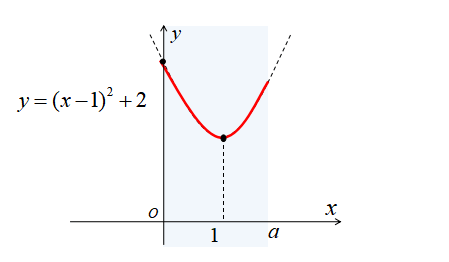
\(1≦a<2\)のとき、\(y=(x-1)^{2}+2\)の軸が定義域に含まれています。なので頂点が最小値になることが図から分かります。
したがって、\(1≦a<2\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0\)のとき、最大値3
\(x=1\)のとき、最小値2
[/st-mybox]
\(a=2\)のとき
\(a=2\)のとき、定義域に含まれるグラフは下図のようになります。
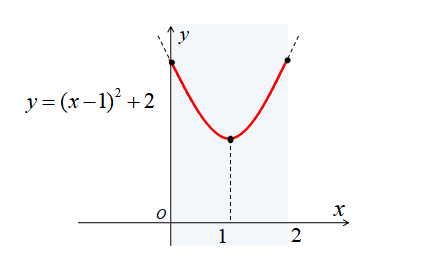
\(a=2\)のとき、図から分かるように最大値をとる点が2つ存在します。
したがって、\(a=2\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0,2\)のとき、最大値3
\(x=1\)のとき、最小値2
[/st-mybox]
\(2<a\)のとき
\(2<a\)のとき、定義域に含まれるグラフは下図のようになります。
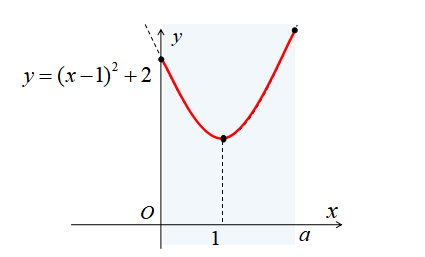
\(2<a\)のとき、定義域の右端が最大値をとるようになります。
したがって、\(2<a\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=a\)のとき、最大値\(a^{2}-2a+3\)
\(x=1\)のとき、最小値2
[/st-mybox]
したがって求める最大値、最小値は
[st-mybox title=”解答” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”10″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a<1\)のとき、最大値3、最小値\(a^{2}-2a+3\)
\(1≦a<2\)のとき、最大値3、最小値2
\(a=2\)のとき、最大値3、最小値2
\(2<a\)のとき、最大値\(a^{2}-2a+3\)、最小値2
[/st-mybox]
この問題のポイントは、\(a\)の値によって最大値・最小値が変わってしまうことです。
文字では分かりづらい方もいると思うので、分かりやすい動画も貼っておきます。
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2次関数の最大・最小⑤ ・ 動く定義域編①
[/st-mybox]
軸に文字を含む場合
最後は軸に文字を含む場合ですが、以下のような問題が出題されます。
[st-mybox title=”軸に文字を含む場合” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a\)は定数とする。関数\(y=2x^{2}-4ax(0≦x≦1)\)の最小値を、次の各場合について、それぞれ求めよう。
(1) \(a<0\)
(2) \(0≦a≦1\)
(3) \(1<a\)
[/st-mybox]
まずは関数を変形します。
\begin{eqnarray}
y&=&2x^{2}-4ax\\
&=&2(x^{2}-2ax)\\
&=&2(x-a)^{2}-2a^{2}
\end{eqnarray}
ここで\(a\)の値によって、以下の3問を解いてみましょう。
(1) \(a<0\)
(2) \(0≦a≦1\)
(3) \(1<a\)
\(a<0\)の場合
\(a<0\)のとき、グラフは下図のようになります。
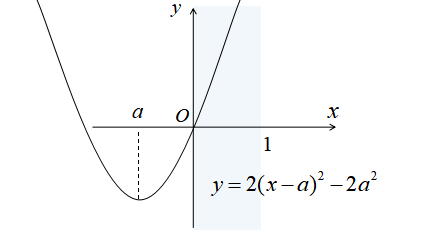
\(a<0\)のとき、\(x=0\)で最小値をとります。
したがって、最小値は\(x=0\)のとき、最小値0
\(0≦a≦1\)の場合
\(0≦a≦1\)のとき、グラフは下図のようになります。
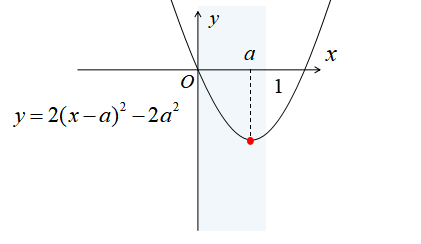
\(0≦a≦1\)のとき、\(x=a\)で最小値をとります。
したがって、最小値は\(x=a\)のとき、最小値\(-2a^{2}\)
\(1<a\)の場合
\(1<a\)のとき、グラフは下図のようになります。
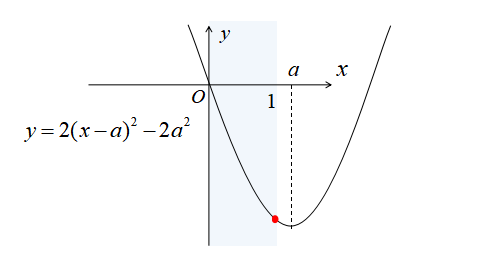
\(1<a\)のとき、\(x=1\)で最小値をとります。
したがって、最小値は\(x=1\)のとき、最小値\(2-4a\)
[st-mybox title=”解答” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a<0\)のとき、最小値0
\(0≦a≦1\)のとき、最小値\(-2a^{2}\)
\(1<a\)のとき、最小値\(2-4a\)
[/st-mybox]
このパターンもかなり複雑だったので、分かりやすい解説動画もつけておきます。
2次関数の最大・最小④ ・ 動く軸編
最大値・最小値《練習問題》

2次関数の最大値・最小値の求め方を4つのタイプに分けて解説しました。
4つのパターンを理解したところで、実際に最大値・最小値を求める練習をしてみましょう。
練習問題1
[st-mybox title=”練習問題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の2次関数の最大値、最小値を求めよう。
\(y=x^{2}+2x+3 (-2≦x≦2)\)
[/st-mybox]
まずは関数を変形します。
\begin{eqnarray}
y&=&x^{2}+2x+3\\
&=&(x+1)^{2}+2
\end{eqnarray}
ここで\(-2≦x≦2\)なので、グラフは下図の実践部分になります。
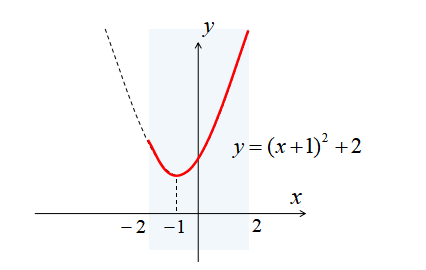
このグラフの実践部分で最大なのは\(x=2\)のときの\(y=11\)
また、実践部分で最小なのが\(x=-1\)のときの\(y=2\)です。
したがって、求める最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=2\)のとき、最大値11
\(x=-1\)のとき、最小値2
[/st-mybox]
練習問題2
[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=x^{2}-4x+1 (0≦x≦a)\)
[/st-mybox]
まずは関数を変形します。
\begin{eqnarray}
y&=&x^{2}-4x+1\\
&=&(x-2)^{2}-3
\end{eqnarray}
ここで\(a\)の値によって、以下の4つの場合分けします。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- \(0<a<2\)のとき
- \(2≦a<4\)のとき
- \(a=4\)のとき
- \(4<a\)のとき
[/st-mybox]
\(0<a<2\)のとき
\(0<a<2\)のとき、定義域に含まれるグラフは下図のようになります。
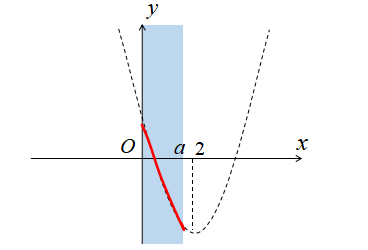
\(0<a<2\)のとき、\(y=(x-2)^{2}-3\)の軸は定義域に含まれていません。
したがって、\(0<a<2\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0\)のとき、最大値1
\(x=a\)のとき、最小値\(a^{2}-4a+1\)
[/st-mybox]
\(2≦a<4\)のとき
\(2≦a<4\)のとき、定義域に含まれるグラフは下図のようになります。
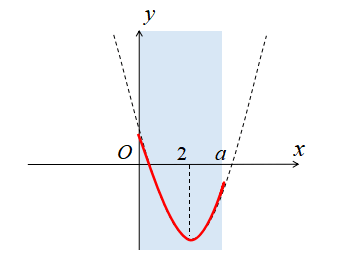
\(2≦a<4\)のとき、最小値は頂点になることが図から分かります。
したがって、\(2≦a<4\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0\)のとき、最大値1
\(x=2\)のとき、最小値-3
[/st-mybox]
\(a=4\)のとき
\(a=4\)のとき、定義域に含まれるグラフは下図のようになります。
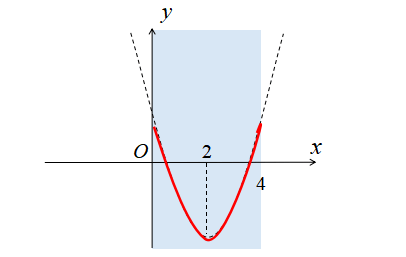
\(a=4\)のとき、最大値をとる点が2つ存在します。
したがって、\(a=4\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=0,4\)のとき、最大値1
\(x=2\)のとき、最小値-3
[/st-mybox]
\(4<a\)のとき
\(4<a\)のとき、定義域に含まれるグラフは下図のようになります。
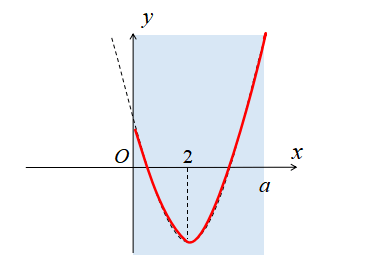
\(4<a\)のとき、最大値は右端の点になります。
したがって、\(4<a\)のときの最大値、最小値は
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(x=a\)のとき、最大値\(a^{2}-4a+1\)
\(x=2\)のとき、最小値-3
[/st-mybox]
よって、\((0≦x≦a)\)における\(y=x^{2}-4x+1\)の最大値、最小値は
[st-mybox title=”解答” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(0<a<2\)のとき、最大値1、最小値\(a^{2}-4a+1\)
\(2≦a<4\)のとき、最大値1、最小値-3
\(a=4\)のとき、最大値1、最小値-3
\(4<a\)のとき、最大値\(a^{2}-4a+1\)、最小値-3
[/st-mybox]
2次関数の最大値・最小値 まとめ
今回は2次関数の最大値・最小値の求め方をまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 20px 0″ myclass=””]最大値・最小値 まとめ[/st-marumozi]
[st-mybox title=”最大値・最小値の4パターン” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 範囲がない場合
- 範囲がある場合
- 範囲に文字を含む場合
- 軸に文字を含む場合
[/st-mybox]
最大値・最小値はまずグラフを書くと解きやすくなる。
範囲や軸に文字を含む場合は場合分けが必要。
関数をみて最大値・最小値を判断するのは難しいです。
実際にグラフを書いてみると最大値・最小値がイメージがしやすくなります。
グラフの平行移動や2次関数の決定は以下の記事で解説しています。
2次関数を総復習したい方はこちらの記事がおすすめです。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

