[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 30px”]
「メネラウスの定理ってどんな公式?」
「メネラウスの使い方が知りたい」
[/st-mybox]
今回は数学1Aの図形の性質から「メネラウスの定理」に関するこんな悩みを解決します。
 高校生
高校生図形の問題はどうしても苦手で…
メネラウスの定理は、三角形と直線の関係についての公式です。
[st-mybox title=”メネラウスの定理” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCと直線DEがあります。
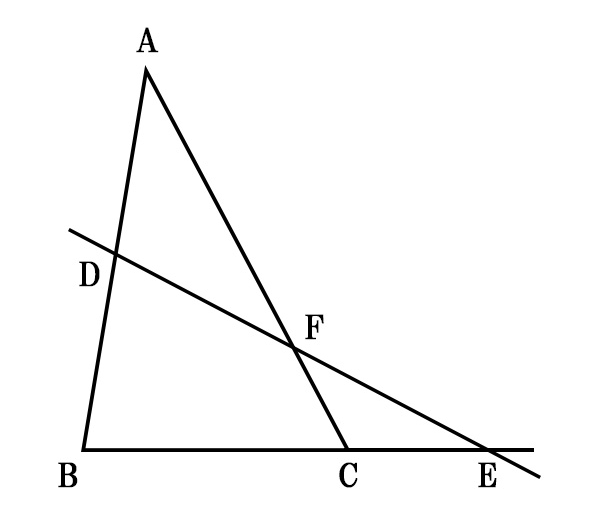
三角形と直線の交点をそれぞれ点D,E,Fで交わるとき
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
[/st-mybox]
メネラウスの定理は公式を知っているだけでパッと答えを出せる便利な公式の1つです。
本記事ではメネラウスの定理の使い方や証明方法、覚え方などについて解説していきます。
また、メネラウスの定理とセットで習う「チェバの定理」についても説明しているので、合わせて参考にしていただければと思います!
 シータ
シータ入塾を検討している方は
ぜひ最後までご覧ください。
それではメネラウスの定理について解説していきましょう。
[st_af id=”13737″]
メネラウスの定理とは
メネラウスの定理とは「三角形」と「直線」の関係についての公式です。
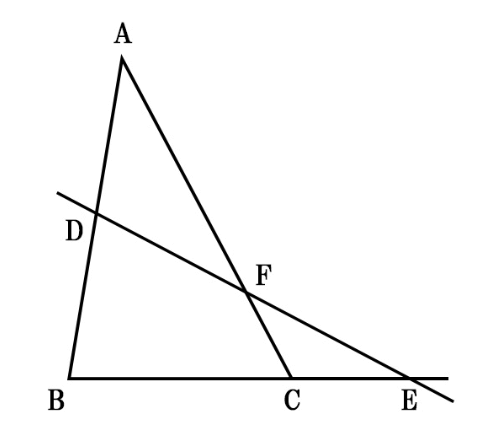
上画像のように「直線」が「三角形」の頂点を“通らず”に2点で交わるとき、以下の式が成り立ちます。
[st-mybox title=”メネラウスの定理” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
三角形と直線の交点をそれぞれ点D,E,Fで交わるとき
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
が成り立つ。
[/st-mybox]
また、上の図では、三角形と直線が交わる場合ですが、交わらない場合でもメネラウスの定理は成り立ちます。
メネラウスの定理(三角形と直線が交わらない場合)
.png)
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”0″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
[/st-mybox]
この内部で交わらないパターンは、なかなか理解するのが難しいと思います。
慣れるまでは、最初に紹介した「三角形と直線が交わるパターン」で理解を進めましょう。
メネラウスの定理の覚え方
「三角形」と「直線」の問題が出てきた時に使える公式ということは、何となく分かりますが、ちょっと覚えづらいかも…と不安になりますよね!
ここでは、定理の覚え方を解説します。
メネラウスの定理の覚え方①
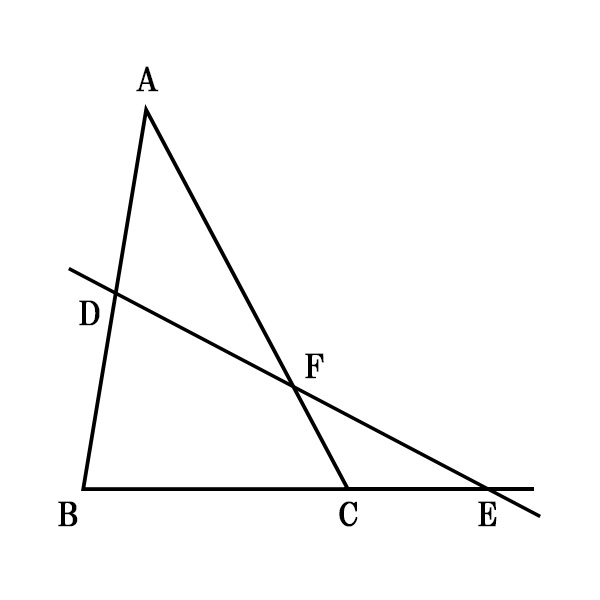
キツネの顔で覚える方法です。下のように赤い部分をキツネの輪郭と考えます。
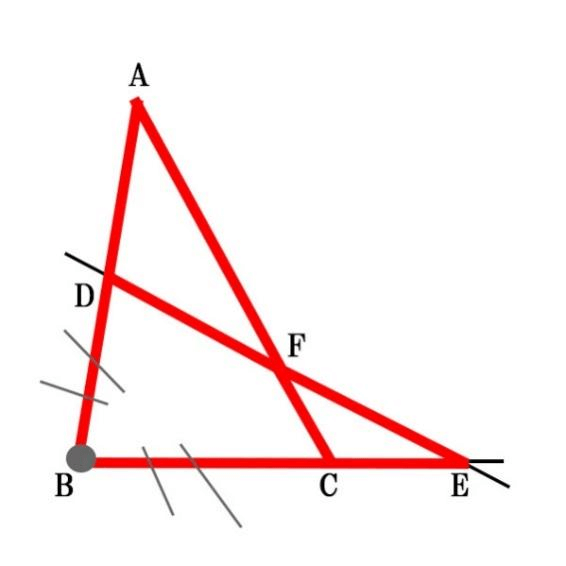
動き方を確認していきましょう。
1.キツネの頭→耳(下側)(①)から始まって、耳→途中(➁)まで戻ります。
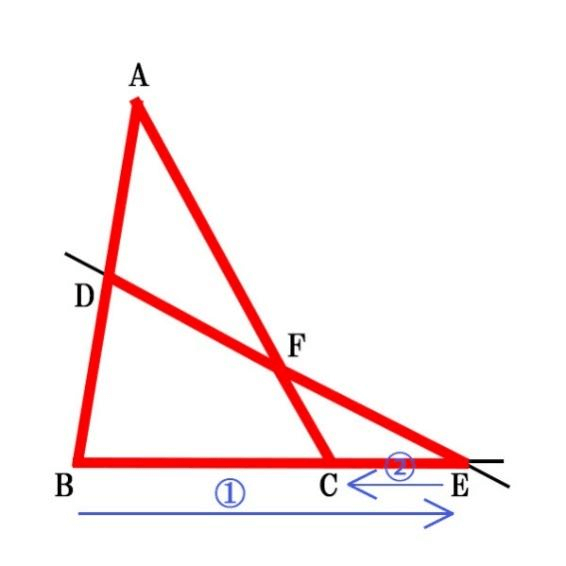
2.そこからは順番に「三角形と直線の交点」→「三角形の頂点」(③→④→⑤→⑥)といった順番です。
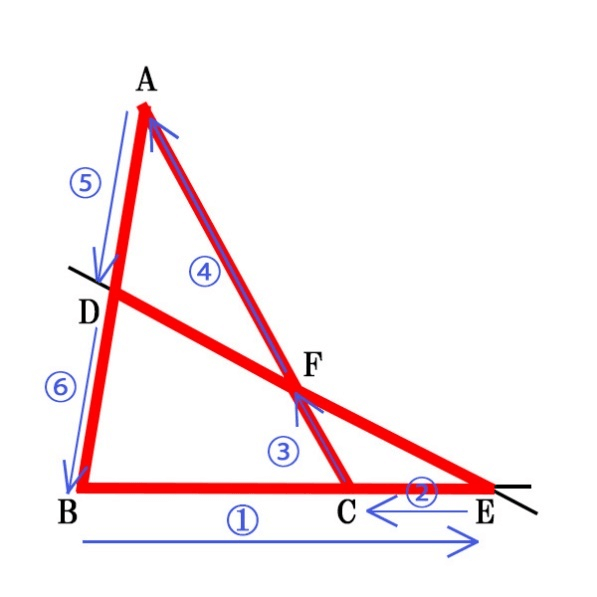
①~⑥を分子分母に以下のように当てはめていきます。
\[\displaystyle \frac{①}{②} \times \frac{③}{④} \times \frac{⑤}{⑥}=1\]
①~⑥に線分を当てはめていきます。
\[\displaystyle \frac{BE}{EC} \times \frac{CF}{FA} \times \frac{AD}{DB}=1\]
アルファベットの順番を追うようにすると、さらに分かりやすく理解できると思いますので、おすすめです。
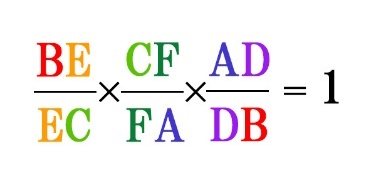
B→E→C→F→A→D→Bといった風に、最初に始まった点に戻ってきます。
順番が分からなくなった場合の参考にしてください。
メネラウスの定理の覚え方②
キツネが分かりづらい人ために別の覚え方も紹介します。
まず三角形の頂点と、直線上にある点を分けます。
ここでは、三角形の頂点を 〇、直線上の点を ☆ とします。
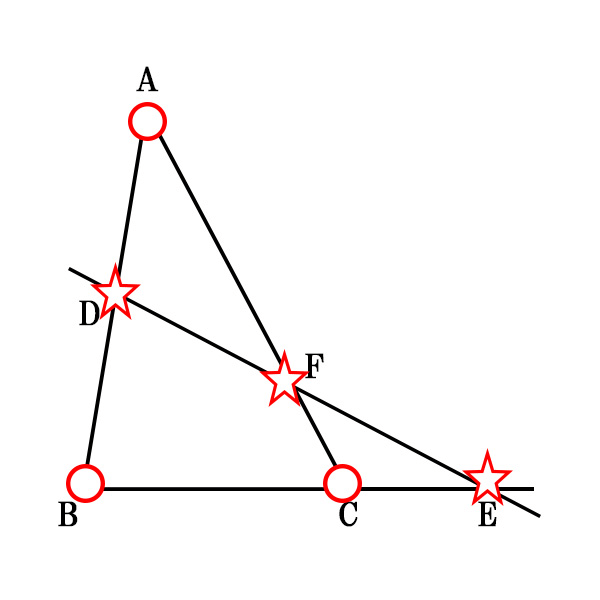
そしたら、点Bから始めて、「三角形と直線の交点」と「三角形の頂点」とを交互に結びます。
〇→☆→〇→☆→〇→☆→〇というイメージです。
すると、メネラウスの定理の式が出来上がります。
\[\displaystyle \frac{BE}{EC} \times \frac{CF}{FA} \times \frac{AD}{DB}=1\]
この覚え方を理解しておくと、「三角形と直線が交わらない場合でも」メネラウスの定理を理解しやすくなります。
ここで、三角形の頂点を 〇、直線上の点を ☆ とします。
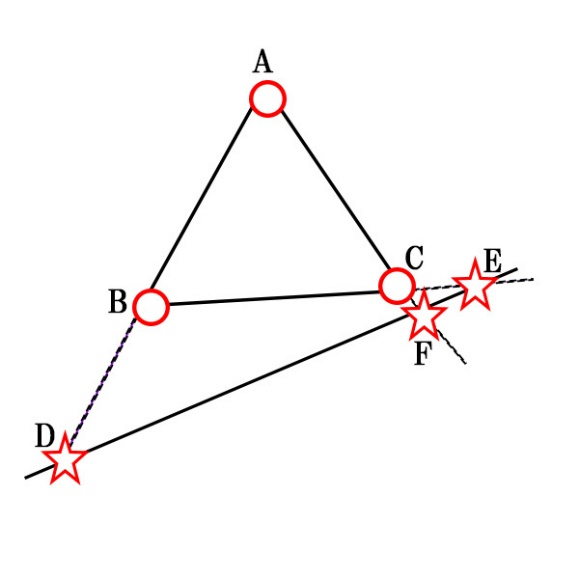
そしたら、点Bから始めて三角形の頂点と直線上にある点を交互に結びます。
先ほどと同じように〇→☆→〇→☆→〇→☆→〇というイメージです。
\[\displaystyle \frac{BE}{EC} \times \frac{CF}{FA} \times \frac{AD}{DB}=1\]
 高校生
高校生僕は覚え方②のほうが分かりやすかったです!
メネラウスの定理の使い方
メネラウスの定理は、図形が絡んでいる問題で「線分の比・長さ」を求める場合に使うことが多いです。
以下の例題でメネラウスの定理の使い方を見てみましょう。
[st-mybox title=”例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
辺ABを3:2に内分する点をD、辺ACを4:1に内分する点をFとする。
このとき、BE:ECを求めよ。
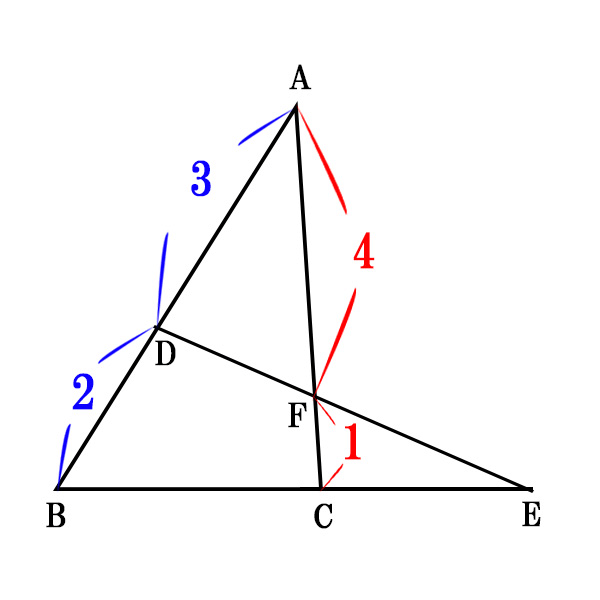
[/st-mybox]
これをメネラウスの定理を使って解いていきます!
まず、線分に関する情報を整理しましょう。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”0″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
辺ABを3:2に内分する点をD → AD:DB=3:2
辺ACを4:1に内分する点をF → AF:FC=4:1
[/st-mybox]
ここでABCに注目してみると、メネラウスの定理が使えます。
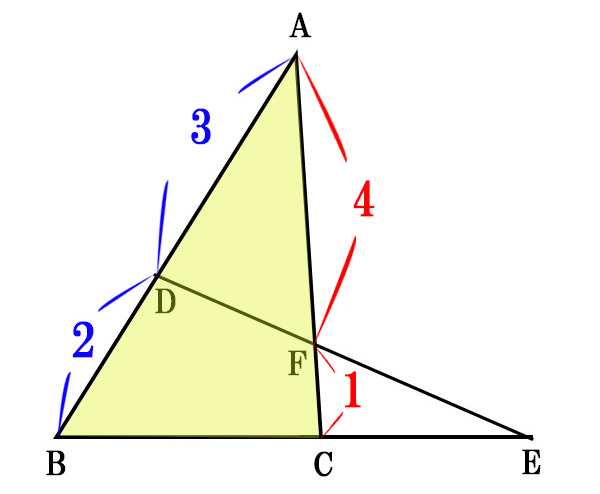
メネラウスの定理より、
\[\displaystyle \frac{BE}{EC} \times \frac{CF}{FA} \times \frac{AD}{DB}=1\]
が成り立ちます。
ここに分かっている情報を代入してみると
\[\displaystyle \frac{BE}{EC} \times \frac{1}{4} \times \frac{3}{2}=1\]
この式を解くと、
\[\displaystyle \frac{BE}{EC}=\frac{8}{3}\]
よって、BE:EC=8:3となります。
 高校生
高校生図形から分かる情報を代入したら解けました!
メネラウスの定理の証明方法
ここでは2つの方法で、メネラウスの定理を証明していきます。
証明①平行線と比の定理で考える
ある「直線」が「三角形」の頂点を“通らず”に 2点で交わるとき、以下の式が成り立ちます。
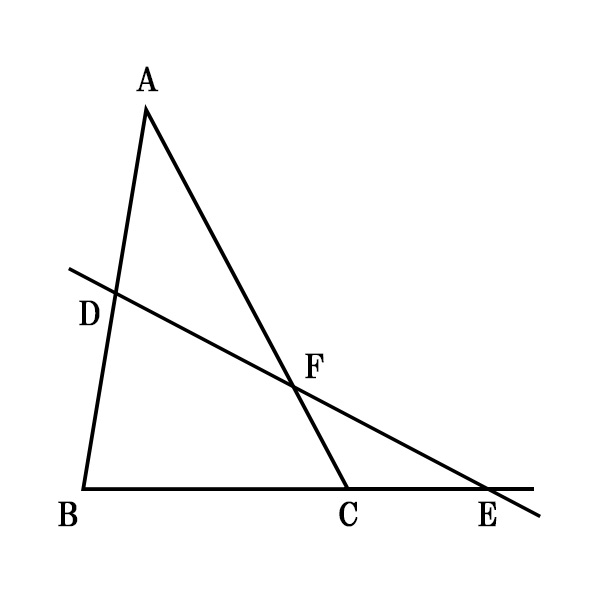
図において、
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
が成り立つことを証明してください。
【証明】
直線に平行な線かつ、点Cを通る直線を引き、この直線と辺ABとの交点をPとします。
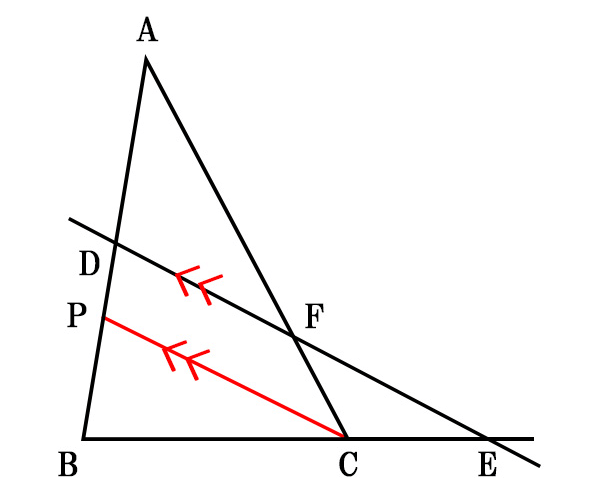
DE//PC、DF//PCより、
\[BE:EC=BD:DP\]
よって、
\[\displaystyle \frac{BE}{EC} = \frac{BD}{DP} \cdots ①\]
また、同様に、PD:DA=CF:FA
よって、
\[\displaystyle \frac{PD}{DA} = \frac{CF}{FA} \cdots ②\]
①➁より
\[\displaystyle \frac{BE}{EC} \times \frac{CF}{FA} =\frac{BD}{DP} \times \frac{PD}{DA}\]
両辺に\(\displaystyle \frac{AD}{DB}\)を掛けて
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=\frac{AD}{DB} \times \frac{BD}{DP} \times \frac{PD}{DA}\]
ここで
\[\displaystyle \frac{AD}{DB} \times \frac{BD}{DP} \times \frac{PD}{DA}=1\]
なので、左辺も同様に
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
となり、メネラウスの定理が成り立つ。
 高校生
高校生平行線を引いて、辺の比で証明するんですね!
証明②面積の比で考える
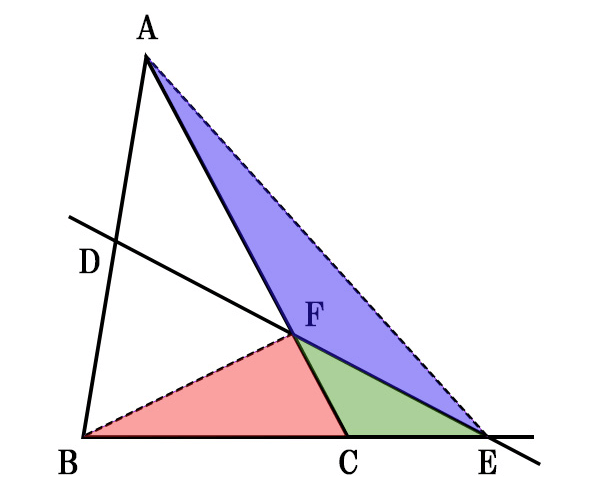
上記画像において、
\[\triangle{BFE}=p\]
\[\triangle{CFE}=q\]
\[\triangle{AFE}=r\]
とする。
\(\triangle{BFE}\)と\(\triangle{CFE}\)は高さが同じ三角形であり、この場合、底辺の長さの比=面積比と成り立つので、
\[\displaystyle \frac{BE}{CE}=\frac{p}{q} \cdots ①\]
同様に、\(\triangle{CFE}\)と\(\triangle{AFE}\)も高さが同じ三角形であるため、
\[\displaystyle \frac{CF}{AF}=\frac{q}{r} \cdots ➁\]
また、\(\triangle{AFE}\)と\(\triangle{BFE}\)は、辺FE(底辺)が共通の三角形である。
底辺が共通の三角形の場合、高さの比=面積比が成り立ちますよね。
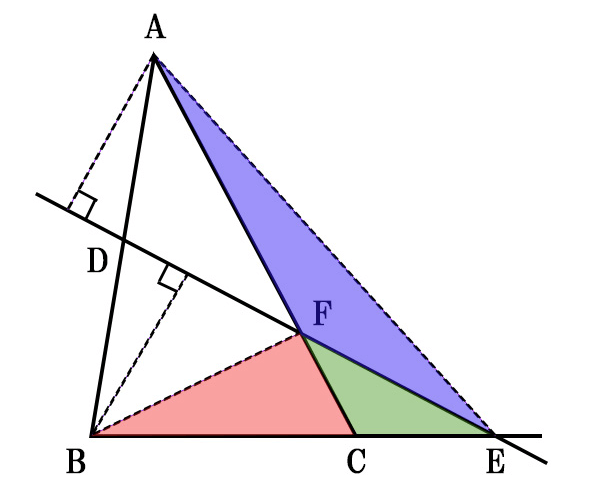
この高さの比は線分AD、DBの比と等しいので、
\[\displaystyle \frac{AD}{DB}=\frac{r}{p} \cdots ➂\]
①➁➂より、
\[\displaystyle \frac{BE}{EC} \times \frac{CF}{FA} \times \frac{AD}{DB}=\frac{p}{q} \times \frac{q}{r} \times \frac{r}{p}=1\]
となり、メネラウスの定理が成り立つ。
 高校生
高校生面積比と辺の比を用いて証明していますね!
メネラウスの定理<練習問題>
メネラウスの定理を使った練習問題に挑戦し、公式の使い方を定着させましょう!
[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
下の図において、以下が成り立つ。
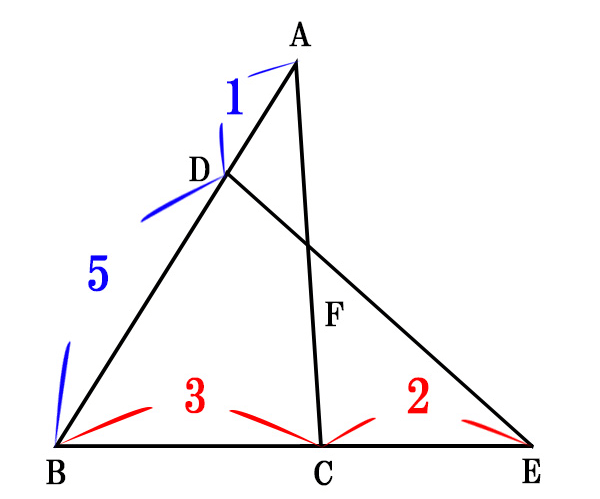
\(BC:CE=3:2\)
\(AD:DB=1:5\)
このとき、線分CFとFAの比を求めよ。
[/st-mybox]
解答
メネラウスの定理より、
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
が成り立つ。
よって、
\[\displaystyle \frac{1}{5} \times \frac{5}{2} \times \frac{CF}{FA}=1\]
これを解くと、CF:FA=2:1
解けましたでしょうか?
もう1問やってみましょう。
[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
下の図において、以下が成り立つ。
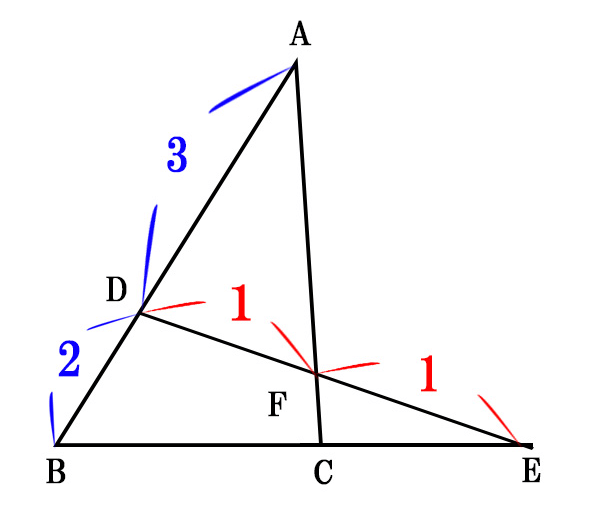
\(DF:FE=1:1\)
\(AD:DB=3:2\)
線分BCとCEの比を求めよ。
[/st-mybox]
この場合は\(\triangle{EDB}\)に直線CAが刺さっていると考えます。
なので、メネラウスの定理は以下のようになります。
\[\displaystyle \frac{EC}{CB} \times \frac{BA}{AD} \times \frac{DF}{FE}=1\]
が成り立つ。
よって、
\[\displaystyle \frac{EC}{CB} \times \frac{5}{3} \times \frac{1}{1}=1\]
これを解くと、BC:CE=5:3
 高校生
高校生向きが変わるとまだ混乱します
 シータ
シータ問題用紙の向きを変えて見やすい向きにすると良いよ!
チェバの定理
メネラウスの定理と同タイミングで習うのが「チェバの定理」ですよね!
ということで、チェバの定理についても解説していきます。
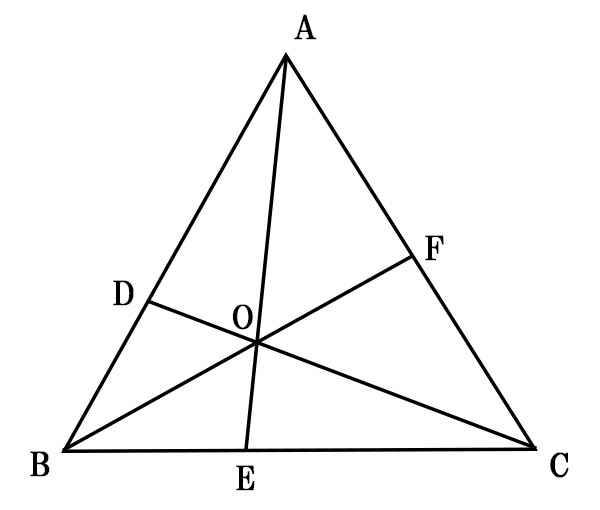
チェバの定理
チェバの定理は、三角形の各頂点から対辺に引いた線分が1点で交わるときに、辺の線分の比に対して成り立つものです。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”0″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
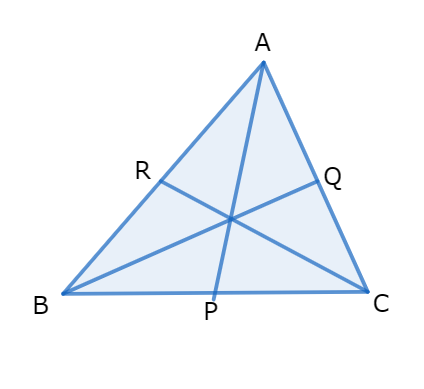
このとき、
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
が成り立つ。
[/st-mybox]
 高校生
高校生チェバの定理は周囲をグルっと回るだけだから覚えやすいです!
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
チェバの定理については別の記事で解説しています。
≫チェバの定理の使い方や証明を解説!簡単に辺の長さが求められる!
[/st-mybox]
メネラウスの定理との使い分け
チェバの定理とメネラウスの定理は似ていますが、これらの使い分けは三角形と直線の関係がポイントです。
メネラウスの定理は、「三角形」と「三角形の頂点を通らない直線」がある図形の問題に対して使うことができます。三角形の頂点を通らない直線については、三角形の外部を通る場合もあります。
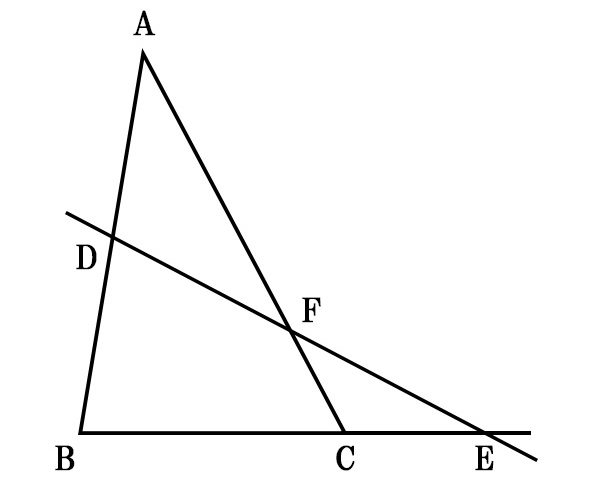
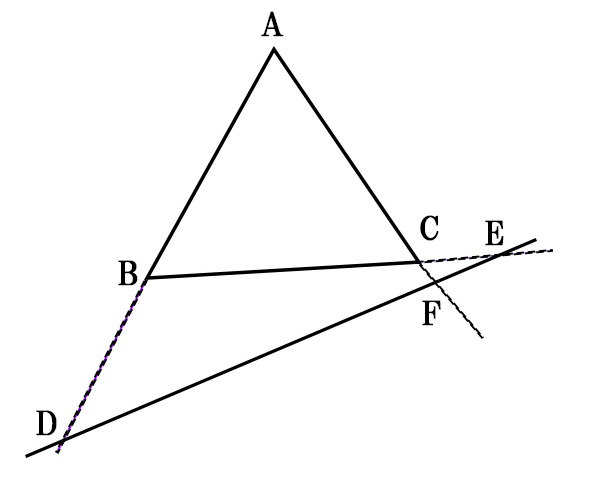
また、チェバの定理は「三角形の頂点から対辺へ下ろした3線が交差する図形」の問題に対して使うことができます。
メネラウスの定理 まとめ
今回はメネラウスの定理についてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 20px 0″ myclass=””]メネラウスの定理まとめ[/st-marumozi]

[st-mybox title=”メネラウスの定理” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
三角形と直線の交点をそれぞれ点D,E,Fで交わるとき
\[\displaystyle \frac{AD}{DB} \times \frac{BE}{EC} \times \frac{CF}{FA}=1\]
[/st-mybox]
メネラウスの定理の覚え方は2つありました。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”1″ borderradius=”1″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
2つの定理の使い分けは以下の通りです。
[st-midasibox-intitle title=”チェバ&メネラウスの使い分け” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
・チェバの定理
⇒三角形の頂点から対辺へ下ろした3線が交差する図形
・メネラウスの定理
⇒「三角形」と「三角形の頂点を通らない直線」がある図形の問題
[/st-midasibox-intitle]
チェバの定理とメネラウスの定理はどちらも辺の比や長さを求める時に使うので、三角形の辺の比や長さを聞かれたら、この2つの定理を思い出してください!
反復練習していけば必ず解けるようになるので学校の問題集でたくさん練習しましょう。
図形の性質についてまとめているのでぜひご覧ください。
[st-card myclass=”” id=”13722″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
♦三角形の五心(内心,外心,重心,垂心,傍心)の性質と証明を解説!
♦三角形の内心とは?内心の意味や座標&ベクトルの求め方を解説
♦三角形の重心の性質と証明!座標とベクトルの求め方も徹底解説!
[/st-mybox]

