今回解決する悩み
「チェバの定理ってどんな公式?」
「チェバの定理の使い方が知りたい」
今回は数学1Aの図形の性質から「チェバの定理」に関するこんな悩みを解決します。
 高校生
高校生図形の問題はどうしても苦手で…
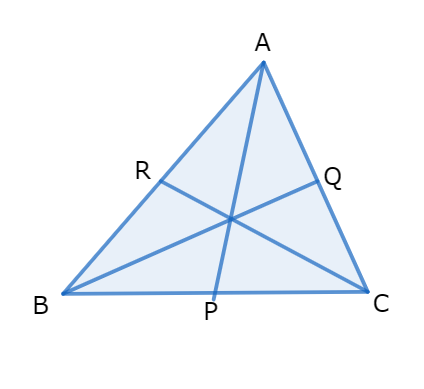
チェバの定理
△ABCの内部に点Oがある。
頂点A,B,Cと点Oを結ぶ直線が、向かい合う辺とそれぞれ点P,Q,Rで交わるとき
\[\displaystyle \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB}=1\]
チェバの定理は各辺の比を用いて、三角形の辺の長さを求める公式です。
本記事ではチェバの定理の使い方や証明方法、覚え方などについて解説していきます。
また、チェバの定理とセットで習う「メネラウスの定理」についても説明しているので、合わせて参考にしていただければと思います!
 シータ
シータ入塾を検討している方は
ぜひ最後までご覧ください。
それではチェバの定理について解説していきましょう。
チェバの定理とは
チェバの定理は辺の比や長さを求める時に使う定理です。
チェバの定理

△ABCの内部に点Oがある。
頂点A,B,Cと点Oを結ぶ直線が、向かい合う辺とそれぞれ点P,Q,Rで交わるとき
\[\displaystyle \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB}=1\]
上記の公式にしたがって、各辺の値を式に代入して積を求めると1になるという定理ですね。
チェバの定理の証明方法
ここからはチェバの定理の証明方法について説明していきます。
まず、△ABCにおいて△OABと△OACに注目して考えます。
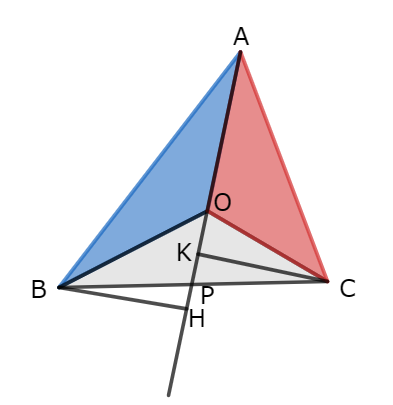
すると、このとき次の等式が成り立ちます。
\[\displaystyle \frac{\triangle{OAB}}{\triangle{OCA}}=\frac{BP}{PC}\]
まずは、これを証明していきます。
【証明】
点B,Cから垂直に下した点をそれぞれH,Kとすると、\(BH // CK\)―①
次に三角形の面積を考えると、
\(\displaystyle \triangle{OAB}=AO \times BH \times \frac{1}{2}\)―②
\(\displaystyle \triangle{OAC}=AO \times CK \times \frac{1}{2}\)―③
②,③でAOと\(\frac{1}{2}\)を消去すると、
\[\triangle{OAB}:\triangle{OAC}=BH:CK―④\]
④より、
\[BH:CK=BP:PC\]
④,⑤より、\(\triangle\ OAB:\triangle OAC=BP:PC\)
これで、
\[\displaystyle \frac{\triangle{OAB}}{\triangle{OCA}}=\frac{BP}{PC}\]
が証明されました。
これと同じように考えると、
\(\displaystyle \frac{\triangle{OAB}}{\triangle{OCA}}=\frac{CQ}{QA}\)―⑦
\(\displaystyle \frac{\triangle{OBC}}{\triangle{OAB}}=\frac{AR}{RB}\)―⑧
となります。
⑥,⑦,⑧より、
\begin{eqnarray}
&&\frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB}\\
&=&\frac{\triangle{OAB}}{\triangle{OCA}} \cdot \frac{\triangle{OBC}}{\triangle{OAB}} \cdot \frac{\triangle{OCA}}{\triangle{ABC}}\\
&=&1
\end{eqnarray}
となり、チェバの定理が証明されました。
チェバの定理の覚え方
ここまで、チェバの定理の証明方法を説明してきました。
ここからは、「チェバの定理、覚えられない!」という人に向けて覚え方をご紹介していきます。
チェバの定理を覚えるうえでのポイントは、図のように「三角形の1つの頂点から、1周するようにアルファベットをたどっていく」ことです。
下の図で説明すると、点Aからスタートして点Aに戻るようにして1周します。
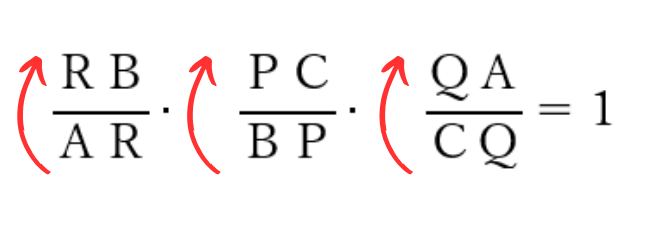
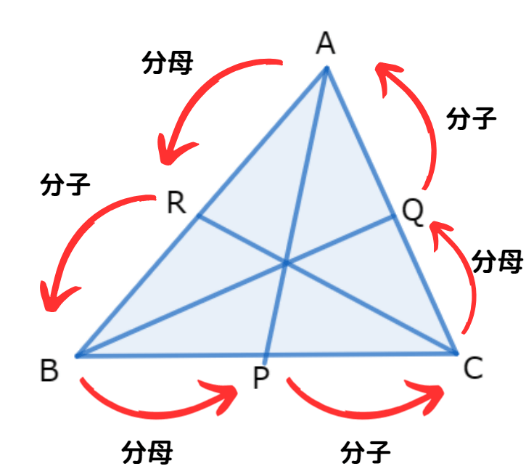
※このときたどっていく向きは時計回りでも、反時計回りでもどちらでも大丈夫です。
チェバの定理はアルファベットの順番がとても大事です。
そのため、順番を間違えると答えが合わなくなってしまいます。
下図の→の順番で式を立てていくと、間違えにくいのではないかと思います。
チェバの定理の使い方
チェバの定理ですが、実際どんなときに使うのか分からない人もいますよね。
ここからは、いつチェバの定理を使えば良いのか、解説していきます。
まず、早速ですがチェバの定理は「三角形の3つの頂点から対辺に向かって引いた3本の線が1点で交わるとき」に使います。

このとき、対辺に向かって引いた線は垂線や角の二等分線である必要はありません。
とにかく3つの線が1点で交わっているときにチェバの定理は発動します。
チェバの定理の練習問題
ここからは、実際に練習問題をやってみましょう!
(1) 次の図においてARの値を求めなさい。
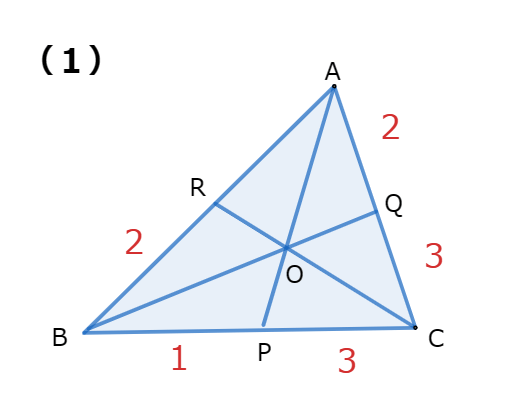
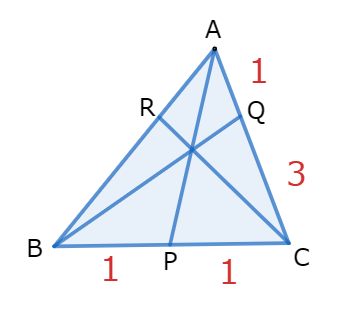
(2) 次の図においてAR:RBを求めなさい。
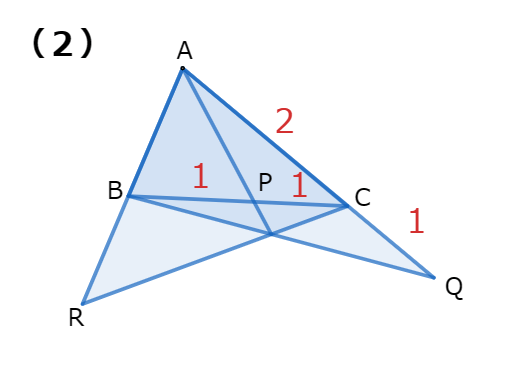
練習問題①の解答
チェバの定理より、
\begin{eqnarray}
\displaystyle \frac{QC}{AQ} \cdot \frac{PB}{CP} \cdot \frac{RA}{BR}&=&1\\
\displaystyle \frac{3}{2} \cdot \frac{1}{3} \cdot \frac{AR}{2}&=&1\\
AR&=&4
\end{eqnarray}
したがって、 AR=4
☆練習問題①の解説
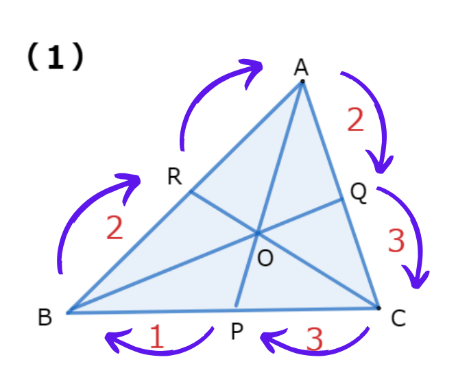
この問題ではチェバの定理を時計回りで考えましたが、反時計回りで考えても良いです。
ですが、式を立てた時に、求めるアルファベットは分子にあった方が計算しやすいと思います。
今回の問題の場合は反時計回りで考えてしまうと、求めるARが分母になってしまい、計算しにくくなります。
\[\frac{2}{AR} \cdot \frac{3}{1} \cdot \frac{2}{3}=1\]
時計回りで考えると、ARが分母になってしまい、計算しにくい。
チェバの定理に慣れてきたら、計算のしやすさも考えながら、解いてみてください。
練習問題②の解答
チェバの定理より、
\begin{eqnarray}
\displaystyle \frac{QC}{AQ} \cdot \frac{PB}{CP} \cdot \frac{RA}{BR}&=&1\\
\displaystyle \frac{3}{1} \cdot \frac{1}{1} \cdot \frac{RA}{BR}&=&1\\
\displaystyle \frac{RA}{BR}&=&3
\end{eqnarray}
したがって、 AR:RB=3:1
☆練習問題①の解説
この問題はこの図のままだとチェバの定理を使うのかわかりにくいと思います。
そのため、ここでのポイントはまず、問題の図を次のような図に書き換えることです。
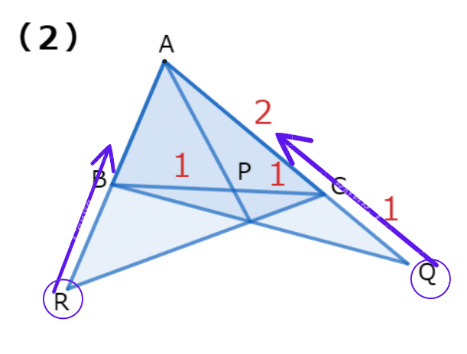
- ➡
注意ポイント
Q,RをそれぞれAC,AB間に入れて考えることによって、チェバ定理を使う問題だということがすぐにわかる図になると思います。
図を書き換えた時に値を書き間違えないように注意してください。
メネラウスの定理も大事!
チェバの定理とセットで習う定理にメネラウスの定理があります。
メネラウスの定理はチェバの定理と混同しやすいので、ぜひこの記事を読んでマスターしてもらえればと思います!
メネラウスの定理とは
メネラウスの定理もチェバの定理と同じく、辺の比や長さを求める時に使う定理です。
<メネラウスの定理>
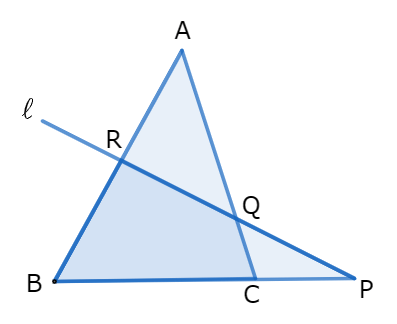
△ABCの辺BC,CA,ABまたはその延長が、三角形の頂点を通らない直線l、それぞれ点P、Q、Rで交わるとき、
\[\displaystyle \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB}=1\]
参考
メネラウスの定理については別の記事で解説しています。
チェバの定理とメネラウスの定理の使い分け
ここまでチェバの定理とメネラウスの定理をご紹介してきました。
でも実際に問題を解こうとすると「チェバとメネラウス、どっちを使えばいいの?」と分からなくなってしまう人がいるかと思います。
2つの定理の使い分けは以下の通りです。
これはどういうことかを図で示します。
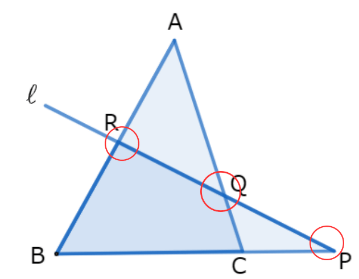
この図を見ると、三角形ABCに直線ℓが重なって、P、Q、RがそれぞれBC、AC、ABで交わっているのがわかると思います。
PはBCの延長線上で交わっています。このような図の時にメネラウスの定理を使います。
チェバ&メネラウスの定理の演習
△ABCについて次の値を求めなさい。
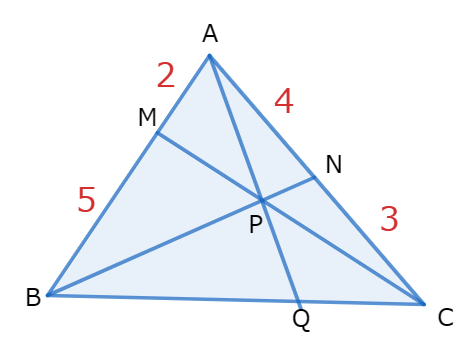
練習問題
(1) PB:PN
(2) BQ:QC
解答①
メネラウスの定理より、
\begin{eqnarray}
\displaystyle \frac{PN}{BP} \cdot \frac{CA}{NC} \cdot \frac{MB}{AM}&=&1\\
\displaystyle \frac{PN}{BP} \cdot \frac{7}{3} \cdot \frac{5}{2}&=&1\\
\displaystyle \frac{PN}{BP}&=&\frac{6}{35}
\end{eqnarray}
したがって、 BP:PN=35:6
☆解説(1)
この問題の難しいところはチェバの定理とメネラウスの定理、どちらを使うのか判断しなければならないことです。
結果から言うと(1)はメネラウスの定理を使います。
まずこの問題は、△ABCではなく、△ABNを主役にして考えます。
△ABNに直線MCが重なっていると考えてください。そこだけを書いた図を載せておきます。
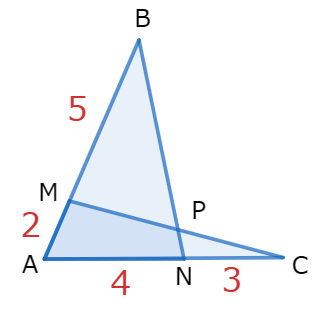
この問題を最初に見た時「チェバの定理を使うのかな?」と思った人もいるのではないかと思います。
しかし、チェバの定理では求めたいBP:PNが式に入らないので、今回の問題はメネラウスの定理を使います。
ポイントは求めたい辺が入るように定理を使うことです。
解答②
チェバの定理より、
\begin{eqnarray}
\displaystyle \frac{NC}{AN} \cdot \frac{QB}{CQ} \cdot \frac{MA}{BM}&=&1\\
\displaystyle \frac{3}{4} \cdot \frac{QB}{CQ} \cdot \frac{2}{5}&=&1\\
\displaystyle \frac{QB}{CQ}&=&\frac{10}{3}
\end{eqnarray}
したがって、BQ:QC=10:3
☆解説(2)
この問題は(1)に比べて分かりやすかったと思います。
まず、今回使うのはチェバの定理です。
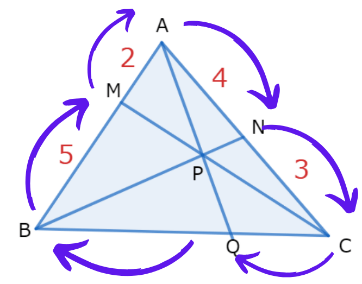
今度は△ABCを主役に考えます。下の図のように点Aから時計回りにチェバの定理を使えば、解ける問題です。
チェバの定理 まとめ
今回はチェバの定理についてまとめました。
チェバの定理まとめ
チェバの定理
△ABCの内部に点Oがある。
頂点A,B,Cと点Oを結ぶ直線が、向かい合う辺とそれぞれ点P,Q,Rで交わるとき
\[\displaystyle \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB}=1\]
チェバの定理の覚え方
「三角形の一つの頂点から、1周するようにアルファベットをたどっていく」ということだけは押さえておいてください。
2つの定理の使い分けは以下の通りです。
チェバの定理とメネラウスの定理はどちらも辺の比や長さを求める時に使うので、三角形の辺の比や長さを聞かれたら、この2つの定理を思い出してください!
反復練習していけば必ず解けるようになるので学校の問題集でたくさん練習しましょう。
図形の性質についてまとめているのでぜひご覧ください。







コメント