重複順列とは？重複順列の公式と使い方

「重複順列ってなに？」
「順列との違いは？」
今回はこんな悩みを解決します。

\(n\)個の異なるものから、重複を許して\(r\)個とる順列を、重複順列といいます。

重複順列は、順列のなかの特殊な並び方の1つです。

本記事では重複順列の公式と使い方を解説します。

後半には練習問題もあるので、ぜひ最後までご覧ください。

重複順列とは？

重複順列とは「重複が許された順列」のことです。

「重複が許された」というのは、同じものを何度も使って良いということです。

これだけではピンとこない人がほとんどだと思うので、順列の問題と重複順列の問題の違いを解説します。

重複順列と順列の違い

具体的に重複順列と順列の問題を比較しましょう。

よくある順列の問題はこのような問題が多いです。

これは4枚のカードそれぞれが1回ずつしか使えないので、重複が許されていないということになります。

2桁の自然数の作り方は、4枚から2枚を取り出して並べるので、

\(_{4}P_{2}=4 \times 3 =12\)

全部で12通りの2桁の自然数の作り方があることが分かりました。

つぎに重複が許された順列、つまり重複順列の場合はこのような問題になります。

同じものを何度使ってもよいとあるので、これは重複が許されているということです。

つまり、重複が許された並び替えの問題なので、重複順列の問題だと分かります。

重複が許されていると、2桁の自然数の作り方も増えます。

順列の時は、同じ数字が使えないので「11」や「22」を作ることはできませんでした。

しかし、重複順列では「11」や「22」「33」も2桁の自然数の1つとして考えます。

つまり、10の位に入る値は1~4の4通りあり、1の位に入る値も1~4の4通りあるので、

\(4^{2}=4 \times 4 =16\)

重複を許した2桁の自然数の作り方は16通りあることが分かりました。

同じものを何度も使ってよいかが、順列と重複順列の違いです。

次に重複順列の公式と使い方を確認していきましょう。

重複順列の公式と使い方

異なる\(n\)種類のものから、重複を許して\(r\)個取り出して並べる順列を、\(n\)個から\(r\)個取る重複順列という。

重複順列では、\(r \leq n\)とは限らず、\(r \gt n\)であってもよい。

文字で説明しても分かりづらいと思うので、例題を解いてみます。

この問題は「重複を許して」と書いてあるので、重複順列の問題だと判断することができます。

３つの数字を重複を許して3ケタの数字を作るので

「111」や「122」のように同じ数字を複数回使うことが許されます。

したがって、

百の位に1,2,3の３パターン

十の位に1,2,3の３パターン

一の位に1,2,3の３パターンとなり

\(3^{3}=3\times{3}\times{3}=27\)

よって27通りの数字が作れることが分かりました。

重複順列と順列では解答が変わるので、しっかりと重複順列であることを見分けられる必要があります。

重複順列の見分け方を確認していきます。

重複順列の見分け方

では重複順列の見分け方について確認していきます。

やはり、一番の違いは同じものを何度も使って良いところです。

頭の中で問題の様子をイメージしたときに、同じものを何度も使って並べていたらそれは重複順列になります。

4種類のカードA,J,Q,Kを重複を許して左から3枚並べる。

{AJQ},{AJJ},{KKA},{KAQ},{AAA}

これは4個のものを重複を許して、3枚並べているので重複順列となり、\(4^{3}\)通り。

一方で、4枚のカードA,J,Q,Kの中から3枚取り出し左から3枚並べる。

{AJQ},{JQK},{AQK},{AJK},{KQJ}

これは4個のものの中から異なる3個を取り出して並べる順列となり、\(_{4}P_{3}\)通り。

こんな問題もあります。

この問題も重複順列の問題なんです。

考え方としては、ボールを1つ取り出す時、ボールを2つ取り出すときのように場合分けして和の法則を使っても良いのですが、

視点を少し変えましょう。

袋の中の６つのボールに注目します。

この問題は取り出して並べるわけではないので、取り出された順番は気にしなくて良いです。

そこで6つのボールに「取り出す」「取り出さない」のシールをつけると考えましょう。

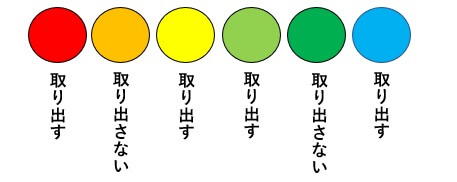
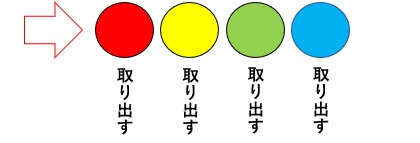
そうすることで、

\[2\times{2}\times{2}\times{2}\times{2}\times{2}=2^{6}=64\]

64通りの取り出し方があることが分かる。

ここで油断してはいけません。

1個以上取り出すときの取り出し方なので、「すべて取り出さない」場合を引く必要があります。

よって\(64-1=63\)

答えは63通りです。

重複順列の見分け方が身についてところで、練習問題に挑戦しよう！

重複順列＜練習問題＞

では、練習問題をやっていきましょう！

解答

硬貨の出方は表か裏の２通りである。

「表・表・表・表・表」のように何回も同じ面が出ても良いので、これは重複順列の問題だと分かります。

よって5回硬貨を投げるときの表と裏の出方は
\(2^{5}=2\times{2}\times{2}\times{2}\times{2}=32\)

したがって、32通りである。

解答
じゃんけんの出し方はグー、チョキ、パーの３通りで、それは４人とも同じです。

したがって、出し方の総数は
\(3^{4}=3\times{3}\times{3}\times{3}=81\)（通り）

重複順列の公式　まとめ

今回は重複順列の公式と使い方についてまとめました。

重複順列と似たものに、重複組み合わせというものがあります。

また、機会があれば重複組み合わせについての記事も書きます。

では、ここまで読んでくださってありがとうございました。