[st-mybox title=”こんな方におすすめ” fontawesome=”fa-file-text-o” color=”#3fc1c9″ bordercolor=”#bae8e8″ bgcolor=”” borderwidth=”3″ borderradius=”5″ titleweight=”bold” title_bordercolor=”#bae8e8″ fontsize=”” myclass=”st-mybox-class st-title-under st-list-border st-list-check” margin=”25px 0 25px 0″]
- 場合の数ってなに?
- 足すのか掛けるのか分からない
[/st-mybox]
「場合の数を求めるのが苦手なんだよね…」
場合の数の数え方には”和の法則”と”積の法則”の2つの数え方しかありません。
実際には、両方の合わせ技で解く問題もありますが、基本的には”和の法則”と”積の法則”をマスターしておけば問題ないです。
本記事を読めば、場合の数の数え方をしっかりとマスターすることができます。
場合の数にまだ不安がある方は、ぜひ最後まで読んでいってください。
場合の数とは
ある事柄Aが起こる確率を知るためには、起こりうる事象が全部で何通りで、Aが起こる場合の数は何通りあるのかを知る必要があります。
なので、事象Aが起こるすべての場合をもれなく、かつ重複なく数える必要があるのです。
例えば、サイコロの目は1~6までの6通り。
しかし、{1、2、3、4、6}と数え洩れがあったり
{1、2、3、4、5、5、6}と重複して数えてしまうと
正確な場合の数ではなくなってしまいますよね。
場合の数を正しく求められないと、
この後の確率でかなり苦戦することになるでしょう。
樹形図
下の図のように道路が通っている町があるとしましょう。


交差点Oから交差点Hまで最短の行き方は何通りありますか?
すべて書き出してみると
全部で6通りであることが分かります。
これでは少し見づらいので、下の図の様に枝分かれの図でも表すことができます。
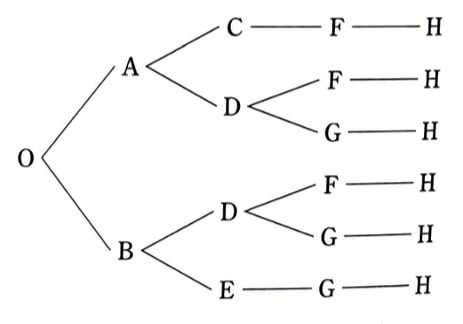
これが樹形図です。

大小2種類のサイコロを投げるとき、目の和が4になる場合は何通りありますか。<解答>
大小のサイコロの出目を樹形図で書き出していく。サイコロの出目の和が4になるときなので、大きいサイコロの目が4以上は確かめなくても良い。よって、(1,3),(2,2),(3,1)の3通りである。
1枚の硬貨を繰り返し投げ、表が2回出たら賞品がもらえるゲームをする。
ただし、投げられる回数は5回までとして、2回目の表が出たらそこで終了とする。
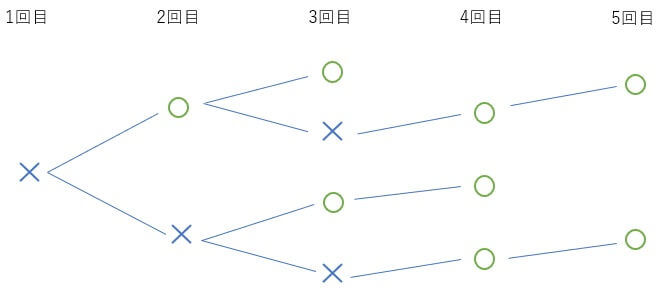
1回目に裏が出たとき、賞品がもらえるための表裏の出方の順は何通りあるか。<解答>
これも頭の中で難しく考えるよりも、実際に樹形図を書いてしまった方が早い。書き出してみるとこのようになり、4通りと分かる。
和の法則・積の法則
場合の数を数えるときに、足す場合と掛け合わせる場合がありますね。
ここで混乱する方が多いのではないでしょうか?
ここからは和の法則と積の法則について解説していきます。
和の法則
2つの事柄AとBの起こり方に重複はないとする。
Aの起こり方がa通りあり、Bの起こり方がb通りあれば、
AまたはBが起こる場合は、a+b通りある。
和の法則の特徴は、2つ事象A,Bが重複しないこと
 高校生
高校生重複ってなんだ…
重複しないというのは、同時に起きないということです
例えば、事象Aを「サイコロの1の目が出る」,事象Bを「サイコロの6の目が出る」だとします。
このときサイコロを1回振って、事象AとBは同時には起きませんよね?
1でもあり6でもある目なんてサイコロにはありえませんね。
したがって、事象Aと事象Bは重複しません。
1個のサイコロを2回投げるとき、目の和が4の倍数になる場合は何通りあるか。目の和が4、8、12になる場合を探していく。4になるのは、(1,3),(2,2),(3,1)の3通り。8になるのは、(2,6),(3,5),(4,4),(5,3)(6,2)の5通り。12になるのは、(6,6)の1通り。よって、和の法則より
\(3+5+1=9\)
A.9通り
積の法則
2種類の飲み物と3種類のケーキからそれぞれ1種類ずつ選ぶ。
飲み物を2種類から選んでからのケーキを3種類から選ぶ。
よって、飲み物とケーキのセットは
\(2 \times 3 = 6\) すなわち 6通りである。
このような「~からの」で繋げられる事象の場合の数を求めるときは、
次の積の法則が成り立つ。
事柄Aの起こり方がa通りあり、そのどの場合に対しても事柄Bの起こり方が
b通りあれば、Aが起こり、そしてBが起こる場合はa×b通りである
大中小3個のサイコロを投げるとき、すべての目が偶数である場合は何通りあるか。<解答>
1個のサイコロで偶数の目の出方は3通りある。よって、積の法則により
\(3\times3\times3=27\)
A.27通り
次の数について、正の約数は何個あるか。
(1) 8
(2) 72<解答>
(1) \(8=2^{3}\)なので、8の約数は\(1,2,2^{2},2^{3}\)である。よって4個である。(2) \(72=2^{3}\times 3^{2}\)なので、72の正の約数は\(2^{3}\)と\(3^{2}\)の約数の積で表される。つまり、\(2^{3}\)の約数は(1)より4個。\(3^{2}\)の約数は\(1,3,3^{2}\)の3個。したがって、積の法則より \(4\times3=12\)
12個である。
場合の数~和の法則・積の法則~おわりに
今回は数学Aの「場合の数」についてまとめました。
教科書に沿った解説記事を挙げていくので、お気に入り登録して定期試験前に確認してください。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!

