[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=””]
「集合の要素ってなんのこと?」
「要素の数え方が分からない」
[/st-mybox]
今回は数Aから、集合の要素についての悩みを解決していくよ!
 高校生
高校生要素の個数というのがイマイチ分からなくて教えて欲しいです。
まずはこちらをご覧ください。
[st-mybox title=”集合の要素” fontawesome=”fa-check” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
集合Aがあります。
\[A=\{1,3,5,7\}\]
このとき集合Aに含まれる、\(1,3,5,7\)を集合の要素といいます。
[/st-mybox]
集合に含まれている数字や文字のことを集合の要素といいます。
つまり、今回のテーマである”要素の個数”というのは、いくつ要素が入っているかを数えるだけの簡単な話です。
定期テストでも得点源にしたい単元なので、この記事を読んで必ず理解してください。
本記事では、集合の要素の個数について解説しています。
 シータ
シータ超基本なので必ず理解しておこう!
集合の要素の個数
まず、集合に含まれる数字や文字を集合の要素といいます。
[st-mybox title=”集合の要素” fontawesome=”fa-check” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
集合Aがあります。
\[A=\{1,3,5,7\}\]
このとき集合Aに含まれる、\(1,3,5,7\)を集合の要素といいます。
[/st-mybox]
そして、要素がいくつ入っているかを”要素の個数”といいます。
\[A=\{1,3,5,7\}\]
この場合だと、1,3,5,7の4つの要素が入っているので、集合Aの要素の個数は4です。
集合の要素の個数は\(n(A)\)と表し、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[A=\{1,3,5,7\}\]
\[n(A)=4\]
[/st-mybox]
となります。
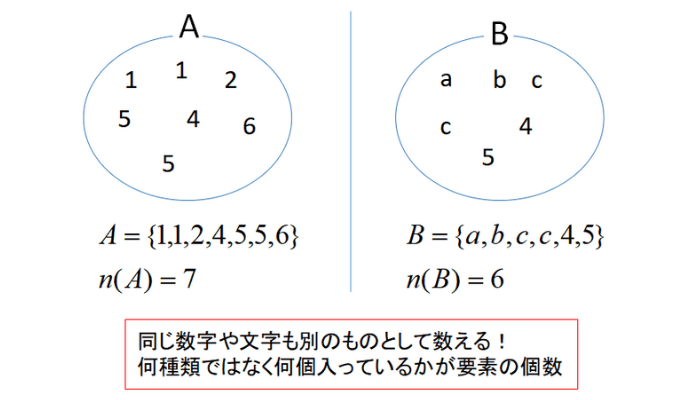
 高校生
高校生要素の種類ではなく、個数なので注意ですね!
共通部分の要素
複数の集合がある場合、重なってるところを共通部分と呼びます。
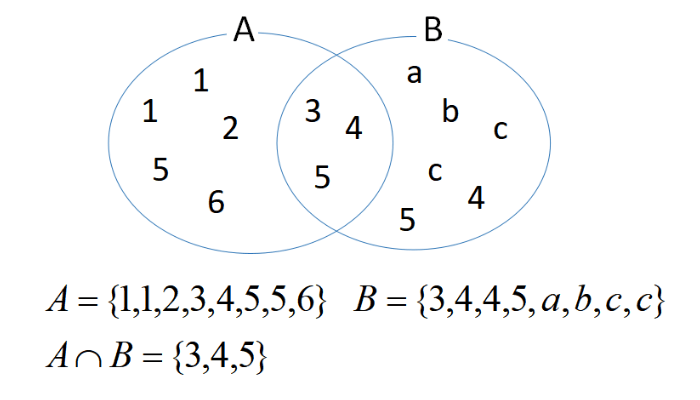
上図の場合、共通部分にある要素は
\[A \cap B=\{3,4,5\}\]
となり、共通部分\(A \cap B\)の要素の個数は
\[n(A \cap B)=3\]
となります。
共通部分と和集合
集合に出てくる記号をしっかり理解できていますか?
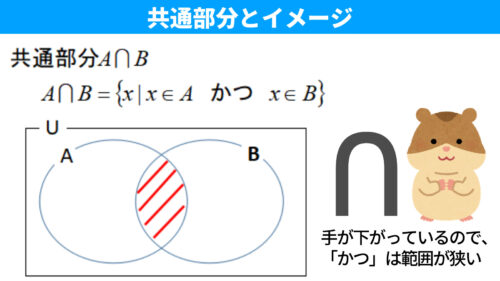
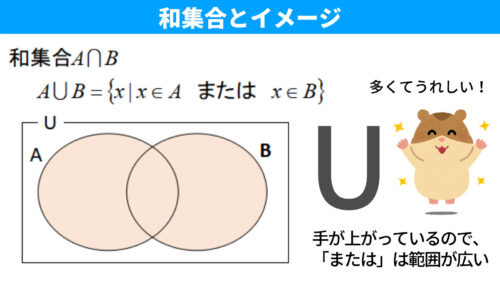
共通部分「AかつB」を\(A \cap B\)、和集合「AまたはB」を\(A \cup B\)として、集合の記号を使って表します。
和集合\(\cup\)の要素
複数の集合がある場合、集合全体のことを和集合といいます。
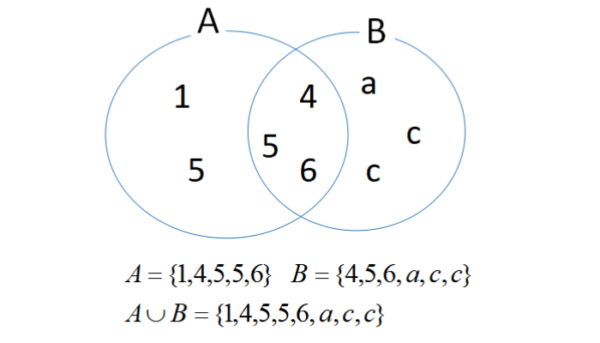
[st-mybox title=”和集合の要素” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\begin{eqnarray}
A&=&\{1,4,5,5,6\}\\
B&=&\{4,5,6,a,c,c\}\\
A \cup B&=&\{1,4,5,5,6,a,c,c\}
\end{eqnarray}
[/st-mybox]
この場合、和集合\(A \cup B\)の要素の個数は
\[n(A \cup B)=8\]
となります。
 高校生
高校生集合の記号で混乱するときがあります
 シータ
シータ集合の記号については別の記事でまとめているよ
[st-mybox title=”関連” fontawesome=”fa-search” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
要素の個数を求める文章題
要素の個数は文章題で出題されることもあります。
[st-mybox title=”要素の個数《文章題》” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
50人の生徒に数学と英語の試験を行った。
数学の合格者は25人,英語の合格者は30人,2科目ともに不合格であった者は5人であった。
(1) 2科目とも合格したのは何人?
(2) 数学だけ合格したのは何人?
[/st-mybox]
意外に思うかもしれませんが、これは集合の問題で問題文をベン図にすると下図のようになります。
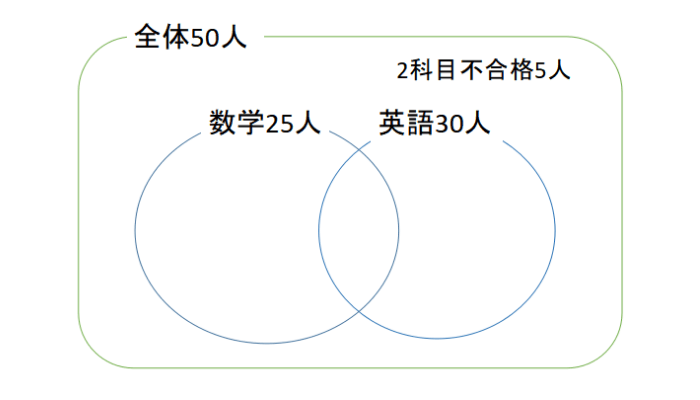
(1) 2科目とも合格したのは何人でしょう。
50人のうち、2教科とも不合格であった者は5人なので、残りの45人は数学、英語のいずれかには合格していることになる。
\[n(数学 \cup 英語)=45\]
にもかかわらず、数学の合格者は25人,英語の合格者は30人を合わせると55人なので、45人を超えています。
この超過分の10人が数学と英語の2科目に合格した人の人数です。
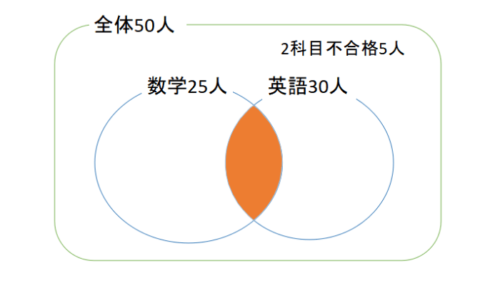
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class scroll-box” margin=”25px 0 25px 0″]
\begin{eqnarray}
n(数学 \cap 英語)&=&n(数学)+n(英語)-n(数学 \cup 英語)\\
&=&25+30-45\\
&=&10
\end{eqnarray}
[/st-mybox]
(2) 数学だけ合格したのは何人でしょう。
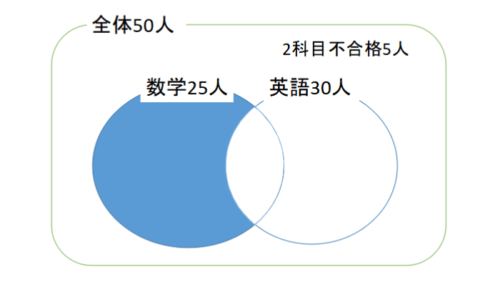
(1)で\(n(数学 \cap 英語)=10\)と分かったので、数学だけに合格したのは残りの15人だと分かります。
以上が、集合の要素の個数を用いた文章題です。
集合の要素の個数《練習問題》

せっかく集合の要素について理解できたので、練習問題に挑戦してもっと理解を深めよう!
[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
100以下の自然数のうち、次のような個数を求めよ。
(1) 3の倍数
(2) 7の倍数
(3) 3の倍数または7の倍数
[/st-mybox]
解説
(1) 3の倍数の個数
100以下の自然数全体の集合をUとして、Uの部分集合で3の倍数を集合A、7の倍数を集合Bとすると、
\[A=\{3\times{1}, 3\times{2},…,3\times{33}\}\]
\[B=\{7\times{1}, 7\times{2},…,7\times{14}\}\]
したがって、100以下の自然数に3の倍数は33個ある。
\[n(A)=33\]
(2) 7の倍数の個数
同様に、100以下の自然数に7の倍数は14個ある。
\[n(B)=14\]
(3) 3の倍数または7の倍数
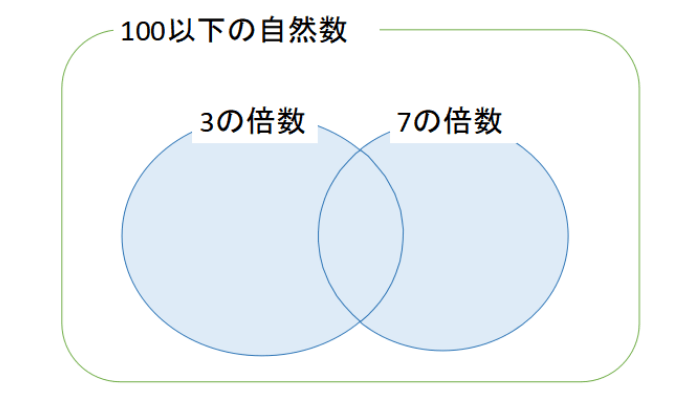
3の倍数または7の倍数なので、求めるのは\(n(A \cup B)\)である。
\[n(A \cup B)=n(A)+n(B)-n(A \cap B)\]
\(n(A \cap B)\)は、「3の倍数かつ7の倍数」なので21の倍数がいくつあるかを求めれば良い。
\[A \cap B =\{21\times{1},21\times{2},…,21\times{4}\}\]
よって、\(n(A \cap B)=4\)
これを用いて
\begin{eqnarray}
n(A \cup B)&=&n(A)+n(B)-n(A \cap B)\\
&=&33+14-4\\
&=&43
\end{eqnarray}
[st-mybox title=”練習問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
100人を対象に、2つの提案a,bの賛否を調べたところ、aに賛成の人は67人
bに賛成の人は84人、aにもbにも賛成の人は60人いた。
aにもbにも賛成ではない人は何人いるか。
[/st-mybox]
解説
この100人を全体集合Uとして、aに賛成の人の集合をA、bに賛成の人の集合をBとすると、
\[n(A)=67 \quad n(B)=84 \quad n(A \cap B)=60\]
aにもbにも賛成でない人の集合は\(\overline{ A } \cap \overline{ B }\)、すなわち\(\overline{ A \cup B }\)である。
\begin{eqnarray}
n(A \cup B )&=&n(A)+n(B)-n(A \cap B)\\
&=&67+84-60\\
&=&91
\end{eqnarray}
よって,
\begin{eqnarray}
n(\overline{ A \cup B })&=&n(U)-n(A \cup B)\\
&=&100-91\\
&=&9
\end{eqnarray}
したがって、aにもbにも賛成ではない人は9人いる。
集合の要素の個数 まとめ

今回は集合の要素の個数について順を追って確認してきました。
意味さえ分かってしまえば、そこまで難しい話でもないのでこの機会で理解しておきましょう。
[st-mybox title=”集合の要素の個数” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class shadow” margin=”25px 0 25px 0″]
\[A=\{1,3,5,7\}\]
\[n(A)=4\]
[/st-mybox]

要素の種類ではなく、要素の個数なので注意です。
集合で使う記号についてはコチラの記事でまとめました。
▼数学A「場合の数と確率」の重要ポイントをまとめた記事を作りました。
[st-card myclass=”” id=”3301″ label=”おすすめ!” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]

