平行移動したい式を入力してください。
y=ax+b
係数を入力してください。
平行移動の移動量を入力してください。
y=ax2+bx+c
係数を入力してください。
平行移動の移動量を入力してください。
a の値は0以外を入力してください。
 高校生
高校生計算に困っていたので助かりました!
今回は2次関数の平行移動に関する悩みを解決します。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”50px auto 40px”]
「平行移動の公式ってなんだっけ」
「2次関数の平行移動って?」
[/st-mybox]
グラフの形を一切変えることなく移動させることを平行移動といいます。
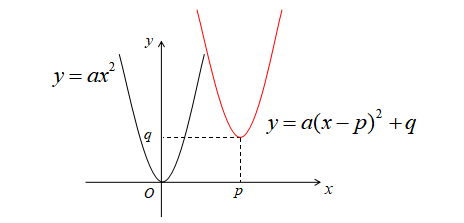
[st-mybox title=”平行移動の公式” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\[y=a(x-p)^{2}+q\]
と表します。
[/st-mybox]
本記事では2次関数の平行移動について解説します。
なぜ平行移動の公式では符号が逆になるのかも解説しているので、ぜひ最後までご覧ください。
2次関数の平行移動
2次関数の平行移動には公式があります。
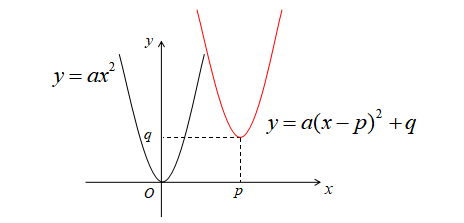
[st-mybox title=”平行移動の公式” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\(y=a(x-p)^{2}+q\)
[/st-mybox]
\(x\)軸方向に\(p\)だけ平行移動するときは、\(x\)を\(x-p\)に置き換えます。
また、\(y\)軸方向に\(q\)だけ平行移動するなら、\(y\)を\(y-p\)に置き換えます。
これで\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\(y=a(x-p)^{2}+q\)となります。
2次関数の軸や頂点を求め方を知っていると、今回の平行移動の公式も理解しやすくなるでしょう。
>>2次関数の頂点・軸を平方完成で求める手順を分かりやすく解説!
 高校生
高校生これは暗記する公式ですか?
 シータ
シータ平行移動は暗記ではなく、使い方を覚えて欲しいかな!
具体例を見せるから使えるようにしよう。
例1 \(y=x^{2}\)を平行移動
[st-mybox title=”例題1” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
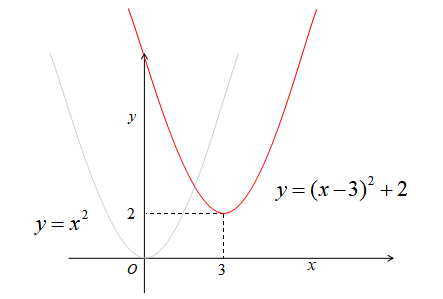
\(y=x^{2}\)を\(x\)軸方向に\(3\),\(y\)軸方向に\(2\)だけ平行移動させる。
[/st-mybox]
この場合、\(x\)を\(x-3\)に置き換えて、\(y\)を\(y-2\)に置き換えます。
[st-midasibox title=”ポイント” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
x &⇒& x-3\\
y &⇒& y-2
\end{eqnarray}
[/st-midasibox]
すると、平行移動した式は以下のようになります。
\[y-2=(x-3)^{2}\]
これを整理して平行移動の完成です。
\[y=(x-3)^{2}+2\]
例2 \(y=-2x^{2}\)を平行移動
次は\(x^{2}\)が係数を持つ場合で考えてみましょう。
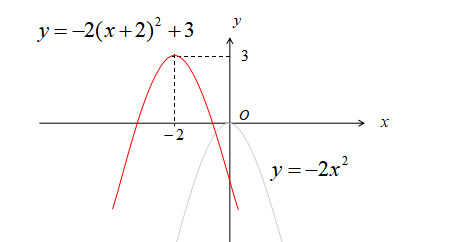
[st-mybox title=”例題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=-2x^{2}\)を\(x\)軸方向に\(-2\),\(y\)軸方向に\(3\)だけ平行移動させる。
[/st-mybox]
\(x\)を\(x+2\)に置き換えて、\(y\)を\(y-3\)に置き換えます。
[st-midasibox title=”ポイント” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
x &⇒& x+3\\
y &⇒& y-3
\end{eqnarray}
[/st-midasibox]
\[y-3=-2(x+2)^{2}\]
これを整理して、
\[y=-2(x+2)^{2}+3\]
例3 \(y=x^{2}+6x+4\)を平行移動
最後にこんな問題も用意しました。
[st-mybox title=”例題3″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=x^{2}+6x+4\)を\(x\)軸方向に\(-2\),\(y\)軸方向に\(3\)だけ平行移動させる。
[/st-mybox]
このとき、\(y=x^{2}+6x+4\)を平行移動させる方法が2つあります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- そのまま平行移動
- 平方完成してから平行移動
[/st-mybox]
方法1.そのまま平行移動
\(x\)軸方向に\(-2\),\(y\)軸方向に\(3\)だけ平行移動するので、
\begin{eqnarray}
y-3&=&(x+2)^{2}+6(x+2)+4\\
y&=&(x^{2}+4x+4)+6(x+2)+4+3\\
y&=&x^{2}+10x+23
\end{eqnarray}
したがって、求める2次関数は
\[y=x^{2}+10x+23\]
だと分かりました。
方法2.平方完成してから平行移動
もう1つのやり方として、平方完成してから移動する方法を紹介します。
まずは\(y=x^{2}+6x+4\)を平方完成します。
\begin{eqnarray*}
y&=&x^{2}+6x+4\\
&=&(x+3)^{2}-9+4\\
&=&(x+3)^{2}-5
\end{eqnarray*}
この関数が\(x\)軸方向に\(-2\),\(y\)軸方向に\(3\)だけ平行移動するので
\(x\)を\(x+2\)に置き換えて、\(y\)を\(y-3\)に置き換えます。
\begin{eqnarray*}
y-3&=&(x+2+3)^{2}-5\\
&=&(x+5)^{2}-5+3\\
&=&x^{2}+10x+23
\end{eqnarray*}
したがって、求める2次関数は
\[y=x^{2}+10x+23\]
となりました。
2つのやり方を紹介しましたが、どちらのやり方でも同じ式になるので安心してください。
 高校生
高校生平行移動のやり方が分かってきました!
なぜ符号が逆になる?
 高校生
高校生どうして(x)軸方向に(p)移動させるのに、(x-p)が出てくるの?
 シータ
シータいい質問だね!なぜそうなるのか解説するよ!
\(x\)軸方向に\(p\)だけ平行移動したときに、なぜ\(x-p\)になるのか疑問に思う方も多いはず。
ひょっとすると、
「\(p\)だけ平行移動したから、\(x+p\)のほうが納得できるんだけど…」
こんな人もいるのではないでしょうか。
🔻ここでは符号が逆になることを解説します。
\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\[y=a(x-p)^{2}+q\]
でしたね。
ここに2次関数\(y=f(x)\)があります。

\(y=f(x)\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものを\(y=g(x)\)とします。

このとき\(y=f(x)\)上のとある点\((x,y)\)は、\(y=g(x)\)上の\((X,Y)\)へ平行移動します。
つまり、以下の2つが成り立っています。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[X=x+p\]
\[Y=y+q\]
[/st-mybox]

これは式変形をすると
\begin{eqnarray}
x &=& X-p\\
y &=& Y-q
\end{eqnarray}
となりますね。
したがって、元の2次関数\(y=f(x)\)に代入すると
\[Y-q=f(X-p)\]
となり、
\[y=f(x-p)+q\]
が成立しました。
したがって、\(x\)軸方向に\(p\)だけ平行移動とき、\(x\)の部分には\(x-p\)が代入されていることが分かります。
難しい話なのでよく分からない方は、公式だけ覚えておけば大丈夫です。
平行移動《練習問題》
2次関数のグラフを平行移動させる練習をしましょう。
今回は以下の3つの式を平行移動してもらいます。
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の2次関数を\(x\)軸方向に3、y軸方向に-2だけ平行移動させたものを求めよう。
- \(y=x^{2}\)
- \(y=-2x^{2}\)
- \(y=x^{2}+x+1\)
[/st-mybox]
\(y=x^{2}\)の平行移動
\(y=x^{2}\)を\(x\)軸方向に3、y軸方向に-2だけ平行移動させると、
\begin{eqnarray*}
y&=&(x-3)^{2}-2\\
&=&(x^{2}-6x+9)-2\\
&=&x^{2}-6x+7
\end{eqnarray*}
したがって、求める2次関数は\(y=x^{2}-6x+7\)
\(y=-2x^{2}\)の平行移動
\(y=-2x^{2}\)を\(x\)軸方向に3、y軸方向に-2だけ平行移動させると、
\begin{eqnarray*}
y&=&-2(x-3)^{2}-2\\
&=&-2(x^{2}-6x+9)-2\\
&=&-2x^{2}+12x-20
\end{eqnarray*}
したがって、求める2次関数は\(y=-2x^{2}+12x-20\)
\(y=x^{2}+x+1\)の平行移動
\(y=x^{2}+x+1\)を\(x\)軸方向に3、y軸方向に-2だけ平行移動させると、
\begin{eqnarray*}
y&=&(x-3)^{2}+(x-3)+1-2\\
&=&(x^{2}-6x+9)+(x-3)-1\\
&=&x^{2}-5x+5
\end{eqnarray*}
したがって、求める2次関数は\(y=x^{2}-5x+5\)
 高校生
高校生おかげで少し慣れてきました!
2次関数のおすすめ勉強法

2次関数は高校数学のなかでも解きやすい問題が多い単元です。
問題の意図をしっかり理解できれば、解法もすぐに思いつけるようになります。
次は2次関数のおすすめ勉強法を紹介します。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#66BB6A” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 教科書やノートを見直す
- 問題集で応用力を磨く
- 分かりやすい解説を見る
[/st-mybox]
自分のいまの理解度と目標を照らし合わせて、自分に合った勉強法を試してみてください。
 シータ
シータ3つの勉強法を紹介するよ
教科書やノートを見直す

まずは基本に立ち返って、教科書・ノートを見直してみましょう。
教科書には重要なポイントがギュッと詰まっています。
2次関数の基本は「2次関数の公式まとめ」にて解説しているのでご覧ください。
 シータ
シータ基本問題が不安なら教科書がおすすめ!
問題集で応用力を磨く

2次関数の関する公式に慣れてきたら、次は問題を解いて応用力を磨きましょう。
- 教科書の例題
- 問題集の基本問題
- 問題集の応用問題
問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。
⇒参考書が読み放題!Kindle Unlimitedについて詳しく知りたい
分かりやすい解説を見る
以下のような悩みがあるなら映像授業もおすすめです。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 勉強しても成績が伸びない
- 学校の授業が分かりにくい
- 分からない所が分からない
[/st-mybox]
映像授業なら自分に必要な授業のみを受けられるうえに、分かるまで繰り返し視聴することができます。
分からないを1つずつ解消していけるので、定期テストで高得点を取りたい方は授業授業がおすすめです。
2次関数の平行移動 まとめ
今回は2次関数の平行移動の公式についてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 20px 0″ myclass=””]2次関数の平行移動まとめ[/st-marumozi]
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
平行移動の公式
\(y=ax^{2}\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させたものは
\[y=a(x-p)^{2}+q\]
[/st-mybox]
 高校生
高校生たくさん例題があったからよく分かったよ!
グラフがイメージできるようになると、最大値・最小値の問題もスムーズに理解できるよ。
最大値・最小値の問題は4つのパターンしかないので、慣れてしまえば得点につなげられます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
>>2次関数の最大値・最小値の求め方!範囲の場合分けで考える方法
[/st-mybox]
2次関数を総復習したい方はこちらの記事がおすすめです。
[st-card myclass=”” id=”5318″ label=”” pc_height=”” name=”基礎から確認!2次関数の公式と重要ポイント” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]

