「箱ひげ図の見方が分からない」
「箱ひげ図の書き方は?」
今回は箱ひげ図に関する悩みを解決していきます。
 高校生
高校生どの線が何を表しているのかよく分からなくて…
データの分析では箱ひげ図からデータの分布を読み取る問題がよく出題されます。
箱ひげ図とは「データの最大値・最小値・四分位数」を表すグラフです。
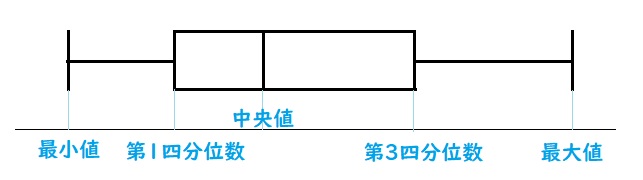
知識がない状態で箱ひげ図を出されるとパニックになりますよね。
本記事では、箱ひげ図の見方や書き方について解説します。
箱ひげ図は1度理解すれば、そこまで難しいグラフではないのでぜひ最後までご覧ください。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#E8F5E9″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]
[/st-mybox]
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
箱ひげ図の見方

箱ひげ図は「データの最大値・最小値・四分位数」を表すグラフです。
箱ひげ図を使うことで、データの分布が分かるようになります。
箱ひげ図には縦の線が5本ありますね。
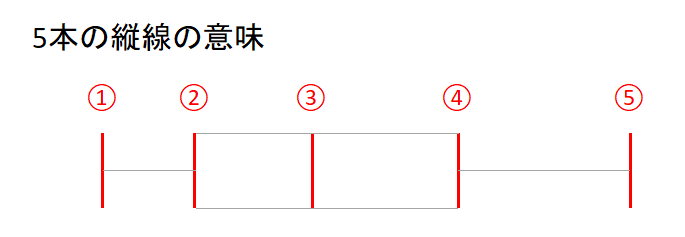
それぞれの線が何を表すのかまとめました。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
①の線\(\cdots\)最小値
②の線\(\cdots\)第1四分位数
③の線\(\cdots\)中央値
④の線\(\cdots\)第3四分位数
⑤の線\(\cdots\)最大値
[/st-mybox]
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
データの平均値も表すときは、箱ひげ図の中にバツ印を書き込みます。
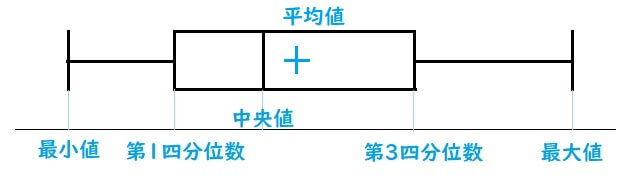
[/st-mybox]
「四分位数って何でしたっけ?」
こんな方も多いと思います。
四分位数とは「データを大きさ順に並べたときに、4等分する位置の値」を指します。
[st-mybox title=”四分位数の求め方” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- データを大きさ順に並べる
- 中央値を求める
- 中央値を境に2等分する
- 下組の中央値,上組の中央値を求める
[/st-mybox]
データを大きさ順に並べて、4等分する値を四分位数といいます。
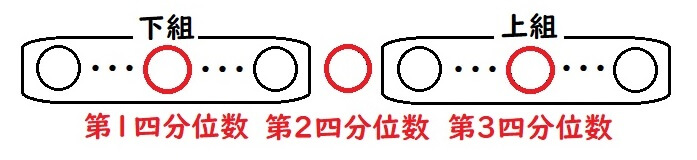
したがって、箱ひげ図の縦線はデータを4等分していて、各線の間には同じ個数のデータが入っています。
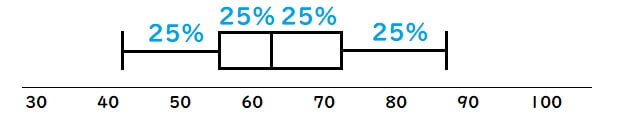
[st-cmemo fontawesome=”fa-lightbulb-o” iconcolor=”#FFA726″ bgcolor=”#FFF3E0″ color=”#000000″ bordercolor=”” borderwidth=”” iconsize=””]データの分布が1点に偏っているとき、箱ひげ図の線と線も近くなります。[/st-cmemo]
四分位数の意味と求め方が知りたい方はこちら
箱ひげ図の書き方
箱ひげ図の書き方を解説します。
[st-mybox title=”箱ひげ図の書き方” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- データを大きさ順に並べる
- 四分位数を求める
- 最大値・最小値・四分位数を数直線上に書き込む
- 四分位数の箱を作る
- 最大値・最小値と箱を結ぶ
[/st-mybox]
では、順を追って一緒に箱ひげ図を書いてみましょう。
以下の表は数学のテストを行った結果です。
| 生徒 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 点数 | 64 | 42 | 58 | 62 | 88 | 56 | 72 |
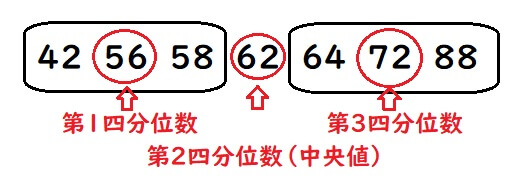
1.データを大きさ順に並び替える
まずはAさん~Gさんを得点が高い順に並び替えます。
[st-mybox title=”テストの点数 小さい順” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
42 56 58 62 64 72, 88 (点)
[/st-mybox]
2.四分位数を求める
データの四分位数を求めましょう。
[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
第1四分位数 \(Q_1\):56
第2四分位数 \(Q_2\):62
第3四分位数 \(Q_3\):72
[/st-mybox]
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
四分位数の意味と求め方は別記事でまとめています。
四分位数の求め方をわかりやすく解説!
[st-card myclass=”” id=”2988″ label=”四分位数” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]
[/st-mybox]
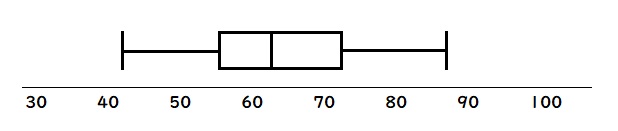
3.最大値・最小値・四分位数を数直線上に書き込む
データの「最大値・最小値・四分位数」を数直線上にメモします。
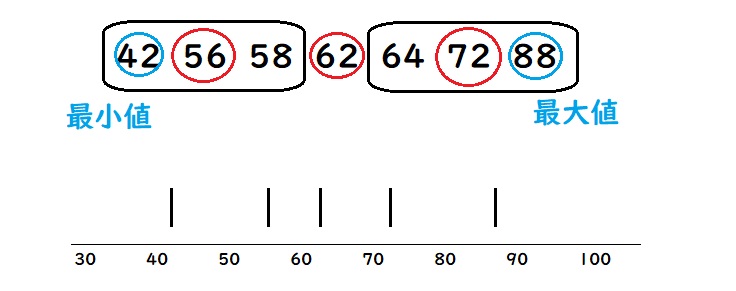
4.四分位数の箱を作る
第1四分位数と第3四分位数をつないで箱の部分を書きます。
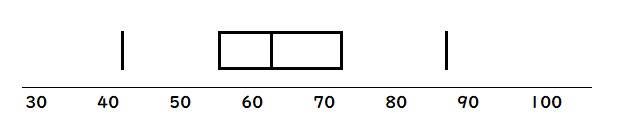
5.最大値・最小値と箱を結ぶひげを書く
最後に最大値・最小値と箱を結ぶひげを書いたら箱ひげ図の完成です。
[st-mybox title=”関連動画” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
箱ひげ図の書き方を解説している動画があったので、ぜひ参考にしてください。
[/st-mybox]
箱ひげ図のメリット
箱ひげ図を使うとデータの分布を簡単に表すことができます。
あるクラスの数学のテスト結果の分布が知りたいとき
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
文章の場合
「生徒それぞれの点数は、42,56,58,62,64,72,88点です。」
表の場合
| 生徒 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 点数 | 64 | 42 | 58 | 62 | 88 | 56 | 72 |
箱ひげ図の場合

[/st-mybox]
箱ひげ図を使うことで、40~90点に集まっていることがすぐに分かりますね。
このように「視覚的にデータ全体の分布を掴むことができる点」が箱ひげ図の大きなメリットです。
 高校生
高校生最大値と最小値が特に分かりやすいですね!
 シータ
シータそうなんだよ!四分位数から全体のバランスも掴みやすいよ!
箱ひげ図の外れ値
データを分析するにあたり、外れ値(極端な値)の扱い方に気を付ける必要があります。
例えば以下のようなデータがあるとします。

このデータを箱ひげ図にするとこのようになります。
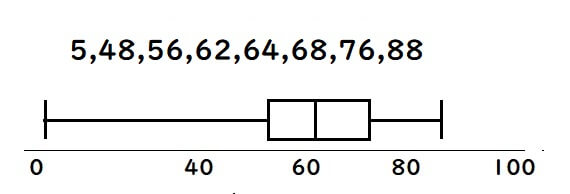
この時、最小値が5なので左に長い箱ひげ図になりました。
このように「最大値・最小値」が外れ値(極端な値)のとき、箱ひげ図は大きな影響を受けてしまいます。

そこで箱ひげ図を作図する際は「上下のひげの長さは箱の1.5倍まで」とします。
それより外にあるデータは外れ値として箱ひげ図に考慮しません。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25p⇩x 0″]
⇩箱ひげ図を作図するなら下図が正解となります。

[/st-mybox]
箱ひげ図<練習問題>

箱ひげ図の意味を理解したところで、練習してみましょう。
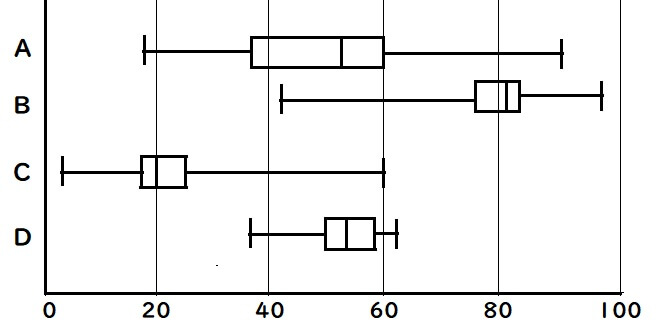
下の図は4種類のテストA,B,C,Dについての、300人の点数を箱ひげ図にしたものです。
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
(1) 80点以上の生徒が半数以上いたのはどのテストですか?
(2) 40点以下の生徒がいて、その数75人未満であったのはどのテストですか?
[/st-mybox]
箱ひげ図における中央値を表す線が80点より右側にあれば、生徒の半数が80点以上だと分かります。
箱ひげ図Bの中央値だけが80点より右側にあるので、問1の答えはBだといえます。
箱ひげ図 まとめ
今回はデータの分析から箱ひげ図についてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]箱ひげ図 まとめ[/st-marumozi]
箱ひげ図とは?
⇒データの「最大値・最小値・四分位数」を表すグラフ

[st-mybox title=”箱ひげ図の書き方” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”#FFFFFF” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- データを大きさ順に並び替える
- 四分位数を求める
- 最大値・最小値・四分位数を数直線上に書き込む
- 四分位数の箱を作る
- 最大値・最小値と箱を結ぶひげを書く
[/st-mybox]
箱ひげ図のメリット
⇒視覚的にデータ全体の分布を掴むことができる点
外れ値の扱い
箱ひげ図を扱う際は「上下のひげの長さは箱の1.5倍まで」

それより外にあるデータは外れ値として箱ひげ図に考慮しません。
今回は箱ひげ図の読み方や書き方についてまとめましたが、データの分析にはたくさん重要な用語があります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
箱ひげ図に合わせて「四分位範囲」や「四分位数」も確認しておきましょう。
まだチェックしていない方はぜひご覧ください。
[st-card myclass=”” id=”3030″ label=”四分位範囲” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[st-card myclass=”” id=”2988″ label=”四分位数” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

