三角形の五心（内心,外心,重心,垂心,傍心）の性質と証明を解説！

[mathjax]

「三角形の五心ってなに？」
「五心の性質を確認したい」
今回はこんな悩みを解決します。

三角形の五心とは、「重心」「内心」「外心」「垂心」「傍心」の5つの点を指します。

五心の中でもよく知られているものと、初めて聞くようなものもありますね。

本記事では三角形の五心それぞれの定義と性質をまとめました。

本記事を読めば三角形の五心について理解できるようにまとめましたので、ぜひ最後まで見ていってください。

三角形の五心

三角形の五心とは、「重心」「内心」「外心」「垂心」「傍心」の５つの点を指します。

5つの点は、それぞれ定義や性質がまったく異なります。

[st-mybox title=”五心の定義” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

重心
“三角形の各頂点から引いた中線の交点”
①中線を2:1に内分する
②3:内部にできる6つの三角形は面積が等しい

内心
“三角形の内角の二等分線の交点”
①内接円の中心
②内心と各辺の距離が等しい

外心
“三角形の各辺の垂直二等分線の交点”
①外接円の中心
②外心と各頂点の距離が等しい

垂心
“各頂点から対辺に向かって引いた垂線の交点”

傍心
“角の二等分線と2つの外角の二等分線の交点”

[/st-mybox]

五心はすべてコンパスと定規で作図できます。

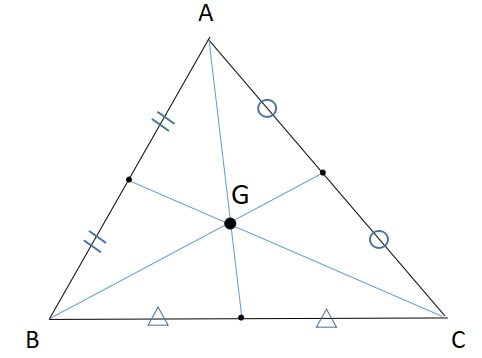
三角形の五心　重心

三角形の重心について解説します。

[st-mybox title=”重心” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

重さの中心の点
英語で「center of Gravity」のため、点Gと表されることが多いです。

[/st-mybox]

重心はスポーツなどでも聞く単語なので、比較的親しみやいですね。

重心の定義は、「3本の中線の交点」です。

[st-mybox title=”三角形の重心の定義” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

三角形の各頂点から引いた中線の交点

[/st-mybox]

中線とは、頂点から向かい合う辺の中点を結んだ線を指します。

[st-mybox title=”三角形の重心　性質” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

1. 頂点と重心を結ぶと、向かい合う辺を二等分する
2. 中線を2:1に内分する

[/st-mybox]

1:頂点と重心を結ぶと、向かい合う辺を二等分する

三角形のある頂点から、重心を通るように直線を結ぶと向かい合う辺を二等分します。

これは重心の定義が、「3本の中線の交点」なので当然の性質です。

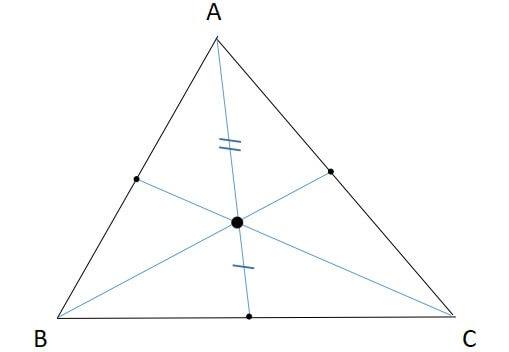
2:中線を2:1に内分する

重心はそれぞれの中心を2:1になるように内分する性質があります。

この性質は中学校で習う、中点連結定理をつかって証明することができます。

三角形の五心　内心

三角形の内心について解説していきます。

内心は「内接円の中心」としてよく知られていますね。

[st-mybox title=”三角形の内心の定義” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

三角形の内角の二等分線の交点

[/st-mybox]

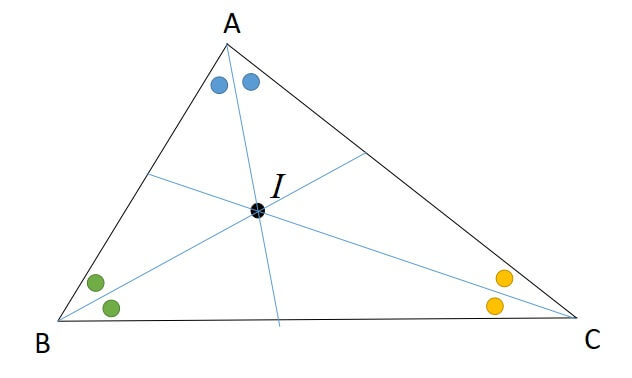
[st-mybox title=”三角形の内心　性質” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

1. 角を二等分する
2. 内心と各辺との距離が等しい
3. 内接円の中心

[/st-mybox]

内心の性質と合わせて、内接円の性質も確認しておくと良いでしょう。

1:角を二等分する

定義が角の二等分線の交点なので、当たり前ですよね

2:内心と各辺との距離が等しい

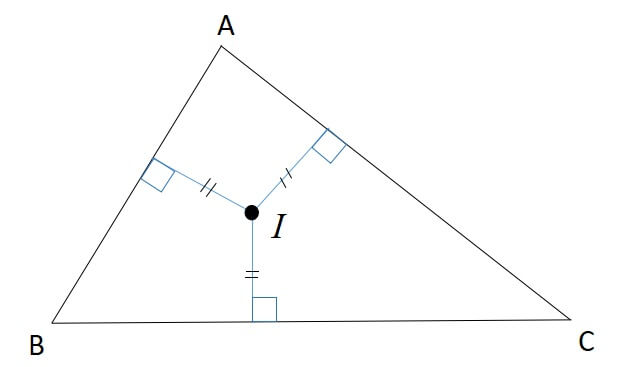
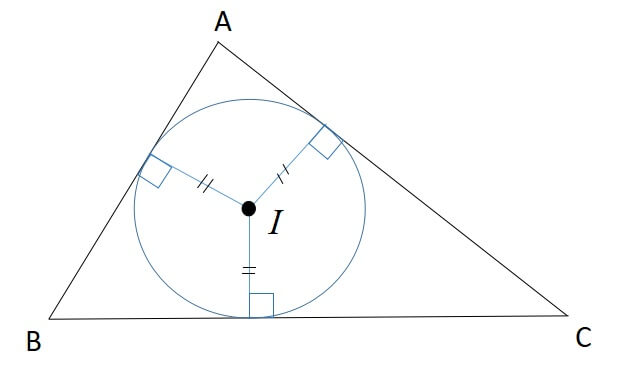
3:内接円の中心

三角形の五心　外心

三角形の外心は油断すると忘れてしまいますよね。

外心は外接円の中心でもあるので要チェックです。

[st-mybox title=”三角形の外心の定義” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

三角形の各辺の垂直二等分線の交点

[/st-mybox]

[st-mybox title=”三角形の外心　性質” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

1. 各辺に垂線を引くと二等分する
2. 外心と各頂点との距離が等しい
3. 外接円の中心

[/st-mybox]

1:各辺に垂線を引くと二等分する

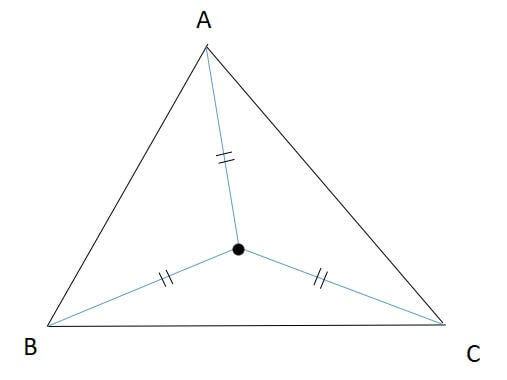
2:外心と各頂点との距離が等しい

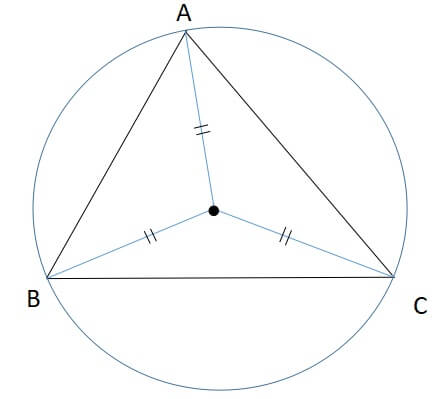
3:外接円の中心

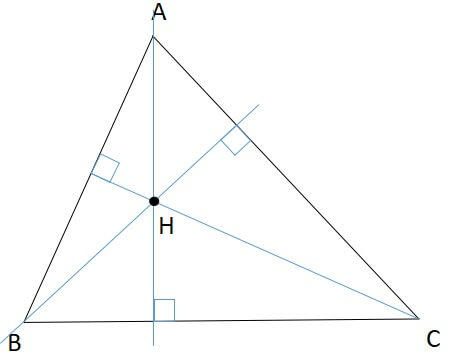
三角形の五心　垂心

三角形の垂心は名前の通り、垂線の集まる点です。

[st-mybox title=”三角形の外心の定義” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

各頂点から対辺に引いた垂線の交点

[/st-mybox]

[st-mybox title=”三角形の垂心　性質” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

1. 四角形ADHF,BEHD,CFHEは円に内接する四角形である
2. \(AH=2RcosA\)

[/st-mybox]

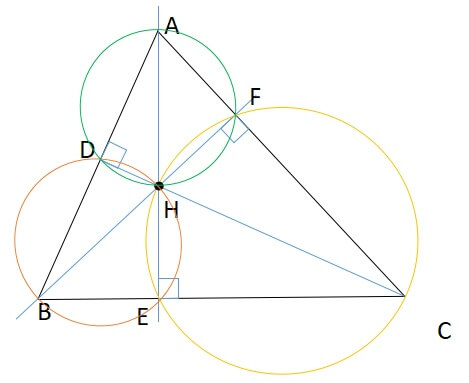
1:四角形ADHF,BEHD,CFHEは円に内接する四角形である

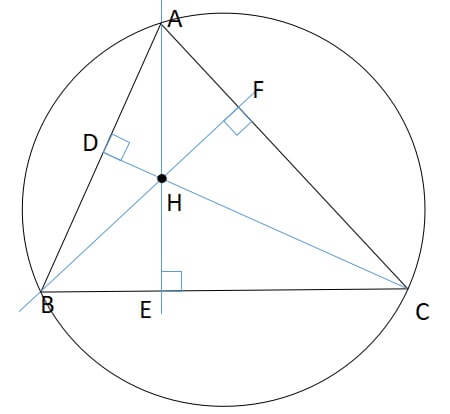
2:\(AH=2RcosA\)
△ABCの外接円の半径をRとする。

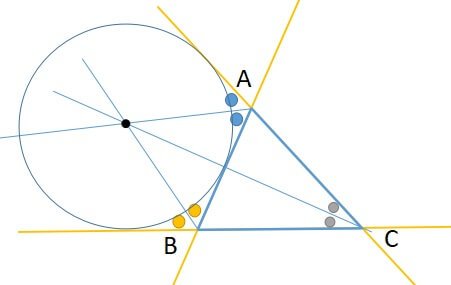
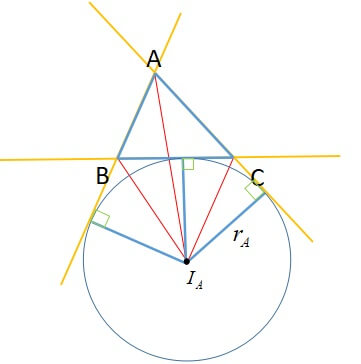
三角形の五心　傍心

おそらく「傍心」が三角形の五心のなかで1番マイナーだと思います。

知っておいて損はないので確認しておきましょう。

[st-mybox title=”三角形の傍心の定義” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

角の二等分線と2つの外角の二等分線の交点

[/st-mybox]

[st-mybox title=”三角形の傍心　性質” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

三角形ABCの面積を\(S\)、\(\displaystyle s=\frac{a+b+c}{2}\)とすると、

\[S=\displaystyle \frac{1}{2} r_{A}(-a+b+c)=r_{A}(s-a)\]

[/st-mybox]

三角形ABCの面積を\(S\)、\(s=\displaystyle \frac{a+b+c}{2}\)とすると、

\[S=\displaystyle \frac{1}{2} r_{A}(-a+b+c)=r_{A}(s-a)\]

五心すべての性質を覚えられるとベストですが、なかなか難しいと思います。

なので「内心」「重心」「外心」は五心の中でも重要なので優先して覚えてください。

三角形の五心　まとめ

今回は三角形の五心についてまとめました。

五心が問題になるときは、それぞれの性質を知っている前提で出題されることが多いです。

ここで紹介した性質だけで十分なので、必ず確認しましょう。

教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。

それでは最後までご覧いただきありがとうございました。

みんなの努力が報われますように！