集合の記号しっかり覚えられていますか?
\(\in\)とか、\(\subset\)とか
形似てるし、覚えづらいですよね。
このページでは、集合の記号押さえておきたい6つの記号と3個の法則をまとめました。
このページを見れば、集合の記号に関する悩みは解決!
それでは、集合の記号について伝えていきたいと思います。
集合の記号6選
集合の記号のなかでも、押さえておきたい6つの記号があります。
1つずつ記号の意味を、図を用いて解説していくので、今回でしっかりと理解していきましょう。
集合の記号1 要素
まずは基礎、要素\(\in\)を紹介します。
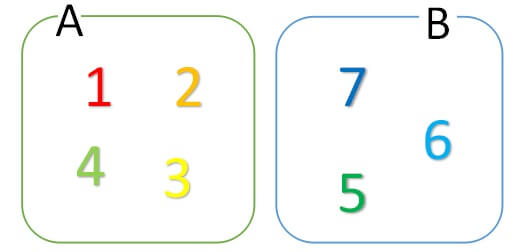
\(a\in A\)と書いたら、aが集合Aの要素であることを表します。
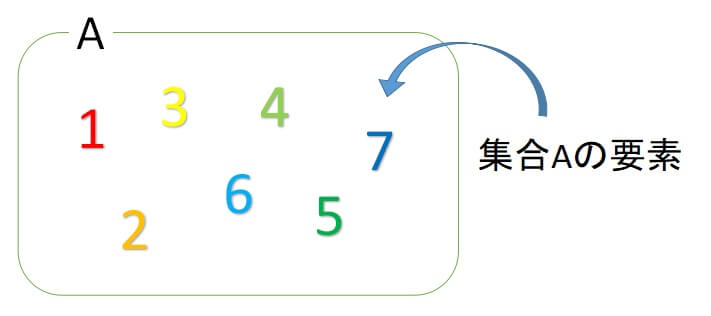
この場合、1,2,3,4,5,6,7が集合Aの要素であり、
\(1,2,3,4,5,6,7\in A\)と表します。
\(\in\)は、次に紹介する\(\subset\)と形が似ているので注意が必要です。
ヨウソのヨに似ていることを覚えましょう。
集合の記号2 部分集合
次に部分集合\(\subset\)を紹介します。
\(B \subset A\)は、集合Bは集合Aの部分集合であるといい、集合Bが集合Aの中に入っていることを意味します。
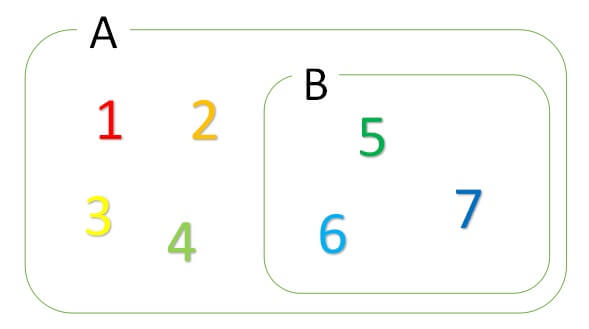
例
A{1,2,3,4,5,6,7},B{5,6,7}のとき、
\(B\subset A\)となります。
大なりと同じく、口が開いている方が大きい集合です。
集合の記号3 \(\cap\) かつ
\(\cap\)は集合の共通部分の集合を表します。
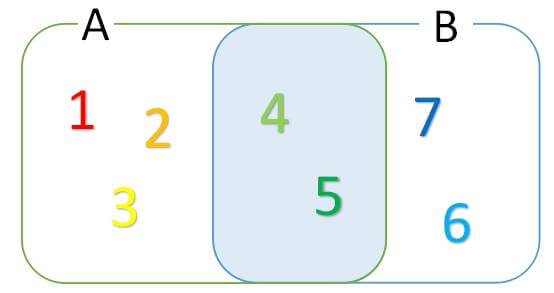
集合A{1,2,3,4,5},集合B{4,5,6,7}のとき
\(A\cap B=\{4,5\}\)となります。
\(A\cap B\)は、集合を表しているので、集合の要素を示すときには{}を付けるのを忘れないように気を付けてください。
集合の記号4 \(\cup\) または
次は、和集合\(\cup\)を紹介します。
\(\cap\)が共通部分だけだったのに対して、和集合\(\cup\)は複数の集合全体の集合を意味します。
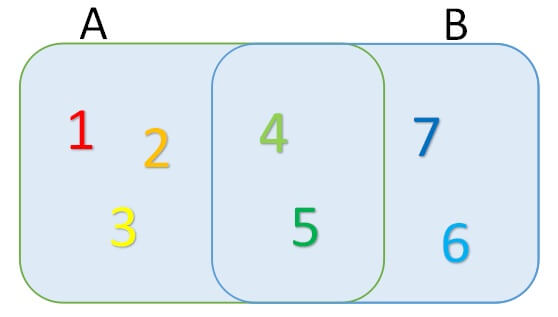
集合A{1,2,3,4,5},集合B{4,5,6,7}のとき
\(A\cup B=\{1,2,3,4,5,6,7\}\)となります。
\(\cap\)と\(\cup\)も似てますよね…
安心してください!覚え方があります。
まず、共通部分\(\cap\)より和集合\(\cup\)の方が要素の数は絶対多いんですよ。
共通部分は重なている部分だけなのに対して、和集合は全体なので当たり前ですよね。
そこで、和集合の方が要素が多くなり嬉しいので、両手挙げて「バンザーイ!!」です。

そして、共通部分は被っている部分なので、「帽子を被っている」ということですね。
ダジャレかよ(笑)
集合の記号5 空集合
一つも要素を持たない集合のことを空集合という。記号は\(\phi\)(ファイ)で表します。
例えば、集合A{1,2,3,4},集合B{5,6,7}のとき
集合Aと集合Bは重なる部分がありませんよね。
なので、\(A\cap B=\Phi\)となります。
集合の記号6 補集合
最後に補集合を紹介します。
集合Aの補集合を\(\overline A\)と表し、A以外の集合を意味します。
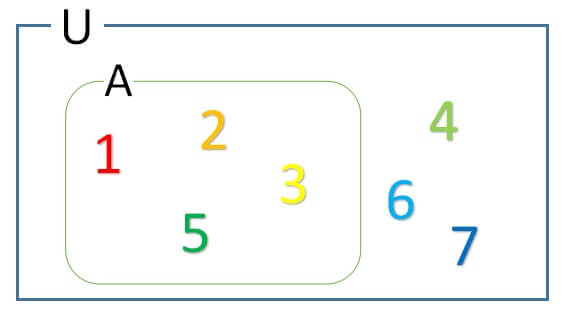
つまり、全体集合U{1,2,3,4,5,6,7},A{1,2,3,5}のとき
\(\overline A=\{4,6,7\}\)となります。
これで押さえておきたい集合の記号6個を紹介しました。
 シータ
シータ最初は教科書を見ながらでも良いから確実に覚えよう!
集合の記号 3個の法則
集合の記号を覚えた次は、定期試験や入試に出やすい集合の3個の法則を解説します。
知っているだけで周りと差がつく法則なので、確実に理解して進めましょう。
集合の法則 ドモルガンの法則
ドモルガンの法則は有名ですよね。
合言葉は、「真ん中ひっくり返してバー分ける」です。
ドモルガンの法則
\(\overline{A \cap B}= \overline{A} \cup \overline{B}\)
\(\overline{A \cup B}= \overline{A} \cap \overline{B}\)
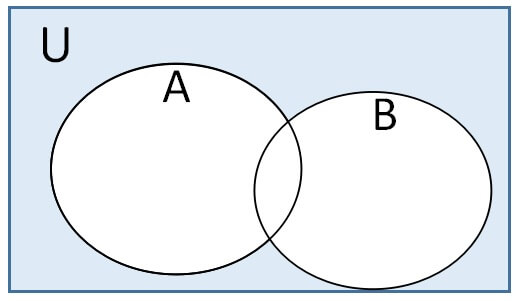
\(\overline{A \cup B}= \overline{A} \cap \overline{B}\)
集合の法則 2集合の和
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
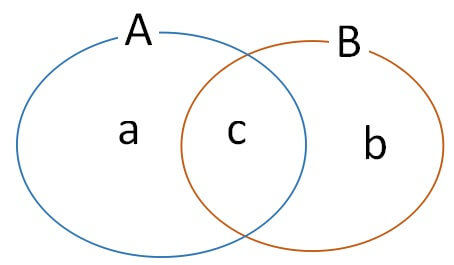
2つの集合の全体集合の要素の個数を求めます。
全体集合なので、\(A \cup B\)の要素の個数が求まればオッケーです。
ここで、\(n(A \cup B)=n(A)+n(B)\)としたら、間違いです。
それだと、真ん中の重なっている部分が2回数えられたことになってしまうので、集合A,Bの共通部分の個数を引く必要があります。
したがって、
2つの集合の全体集合の個数を求めるときは、
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
集合の法則 3集合の和
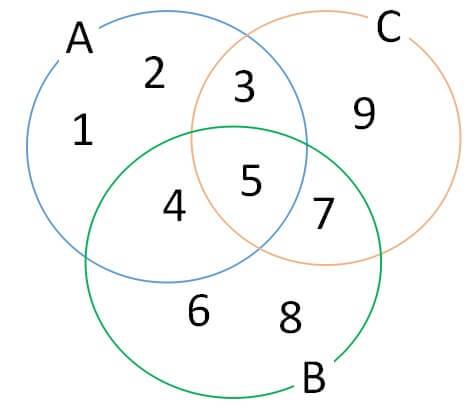
つぎは3つの集合の全体集合の要素の個数を求めていきます。
主な考え方は2つの時と変わりません。
全部足しただけだと、重複して数えられている部分があるので、その分を引く作戦です。
そこで、
こうなったら、間違いです。
実は、
このままだと、真ん中を引きすぎているんです。
2つの集合が重なった部分は1回引けばよいんですが、
真ん中は3つの集合が重なった後に、3回引かれているので、このままだと真ん中に穴が開いています。
したがって、最後に3集合の共通部分を加えてあげることで、3集合の全体集合の要素の個数を求めることができます。
集合の記号《練習問題》

では、今日覚えたことを使って練習問題を解いてみましょう。
A{1,2,3,4},B{3,4,5,6,7}のとき、次の集合の要素を求めよ。
(1) \(A\cap B\)
(2) \(\overline{A \cup B}\)2.2つの集合A,Bがある。
それぞれ集合の個数が\(n(A)=47\),\(n(B)=35\),\(n(A\cap B)=26\)のとき、和集合\(A\cup B\)の要素の個数を求めよ。
解答
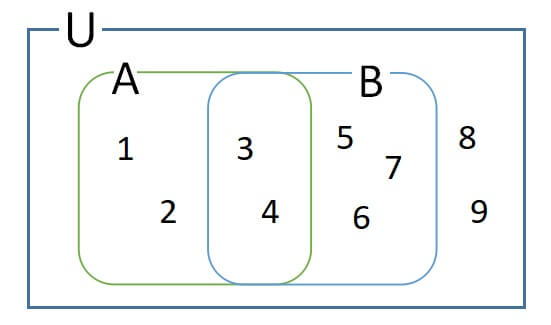
1.図を書くとわかりやすいです。
(1) \(A\cap B=\{3,4\}\)
(2) \(\overline{A \cup B}=\{8,9\}\)
2.これは押さえておきたい3つの法則の1つですね。
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)でしたので、
\(n(A \cup B)=47+35-26=56\)
答えは、56個となります。
集合の記号 まとめ
| 名称 | 意味 | |
|---|---|---|
| \(a\in A\) | 要素 | aは集合Aの要素である。 |
| \(B\subset A\) | 部分集合 | 集合Bは集合Aに含まれる。 |
| \(A\cap B\) | 共通部分 | 集合Aにも集合Bにも属する集合。 |
| \(A\cup B\) | 全体集合 | 集合Aまたは集合Bに属する集合。 |
| \( \Phi \) | 空集合 | 要素を1つも持たない集合。 |
| \(\overline{A}\) | 補集合 | 集合Aに属さない集合全体。 |
集合の記号まとめ
数学Aの集合の記号押さえておきたい6つの記号&3個の法則をまとめてきました。
集合は記号の意味を覚えておけば、点数が取りやすい単元なので、今回紹介したものはこの機会に覚えておきましょう。
他にも教科書に内容に沿ってどんどん解説記事を挙げていくので、
お気に入り登録しておいてもらえると定期試験前に確認できると思います。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!










コメント
コメント一覧 (0件)
文中には、次の送りガなの誤りがあります。
「間違え」の送り仮名は、正しくは「間違い」です。
「え」と「い」の使い分けが逆転する方は、北陸地方から新潟県の出身者かな。
古今和歌集が編纂されたころは、「い」を「え」と発音し表記していたようです。明治政府になって、現在の常用漢字につながる統一的な表記が普及し始めたようです。
ご指摘ありがとうございます。
修正いたしました。
集合の”=”は直感的には高校までで集合以外の単元で出てくる=と同じですが、特に互いに部分集合であるとき”=”が使われます。集合の等号を証明する問題が万が一出た場合は互いに部分集合であることを示しましょう。