三角比の重要単元まとめ！数学Ⅰ

2025年10月16日

数学Ⅰ図形と計量で欠かせないのが『三角比』ですよね。

[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 40px”]

「三角比が苦手」
「三角比の総復習がしたい」

[/st-mybox]

今回は三角比に関するこんな悩みを解決します。

高校生

三角比が苦手なんです…

今回は三角比の基礎が詰まった「完全攻略」記事を書きました。

長い記事ですがゆっくり読めば三角比の総復習ができるようになっています。

シータ

気になる見出しをクリックして、
ぜひ最後までご覧ください。

[st_af id=”13737″]

三角比の重要公式一覧

まずは『三角比』において確実に押さえたい
重要な公式5つをリストアップしました。

三角比の公式を大急ぎで知りたい方はこちらをご覧ください。

[st-mybox title=”三角比の公式” fontawesome=”fa-check-circle” color=”#ffca20″ bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

三角比の基本公式
三角比の相互関係
正弦定理
余弦定理
$\sin$を用いた三角形の面積

[/st-mybox]

三角比の基本公式

三角比($\sin,\cos,\tan$）の基本公式で、三角比を学んでいく上では欠かせない公式です。

[st-mybox title=”三角比の公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

$\sin \theta =\displaystyle \frac{y}{r}$
$\cos \theta =\displaystyle \frac{x}{r}$
$\tan \theta =\displaystyle \frac{y}{x}$

[/st-mybox]

＞もう少し詳しく

三角比の相互関係

三角比は$\sin,\cos,\tan$のいずれかの値が分かっていれば以下の相互関係から他の2つの求めることができます。

[st-mybox title=”三角比の相互関係” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

$\sin^{2} \theta+\cos^{2} \theta=1$

$\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}$

$\displaystyle 1+\tan ^{2} \theta=\frac{1}{\cos ^{2} \theta}$

[/st-mybox]

＞もう少し詳しく

正弦定理

正弦定理は外接円の半径を求める公式でありながら、各辺の長さや角の大きさを求めるときにも活用します。

[st-mybox title=”正弦定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

△ABCの外接円の半径をRとすると、次が成り立つ。

\[\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]

[/st-mybox]

＞もう少し詳しく

余弦定理

余弦定理を用いることで、各辺の長さや角の大きさを求めることができます。

[st-mybox title=”余弦定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

△ABCにおいて、次が成り立つ。

$a^{2}=b^{2}+c^{2}-2bc \cos \angle A$

$b^{2}=a^{2}+c^{2}-2ac \cos \angle B$

$c^{2}=a^{2}+b^{2}-2ab \cos \angle C$

[/st-mybox]

＞もう少し詳しく

$\sin$を用いた三角形の面積

2つの辺の長さとその間の角の大きさが分かっているとき、以下の公式を用いて三角形の面積を求めることができます。

[st-mybox title=”sinを用いた面積公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

$sinを用いた面積公式$

2辺の長さ a, b とその間の角 A の三角形の面積は
\[
\begin{aligned}
S &=\frac{1}{2} b c \sin A \\
&=\frac{1}{2} c a \sin B \\
&=\frac{1}{2} a b \sin C
\end{aligned}
\]

と表すことができる。

[/st-mybox]

＞もう少し詳しく

上で紹介した公式はどれも三角比に欠かせない重要な公式です。

三角比の公式

三角比は$\sin$（サイン）や$\cos$（コサイン）という記号を使って表現します。

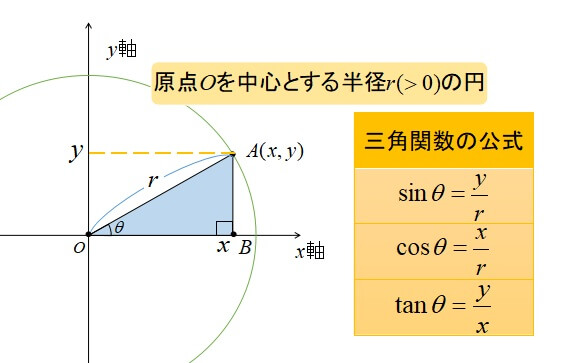
以下の三角比の公式は覚えておかないと、手も足も出ないので必ず覚えてください。

$\sin \theta =\displaystyle \frac{y}{r}$
$\cos \theta =\displaystyle \frac{x}{r}$
$\tan \theta =\displaystyle \frac{y}{x}$

[/st-mybox]

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数学Ⅱの三角関数では中心角を$360^\circ$ではなく、$2\pi$と表します。

この表し方は弧度法といい、弧度法とは？弧度法の変換や面積公式すべて解説！で解説しています。

したがって、$180^\circ=\pi$、$60^\circ=\displaystyle \frac{\pi}{3}$のようになります。

[/st-mybox]

三角比の公式を使いこなせるように実際に数字を代入してみましょう。

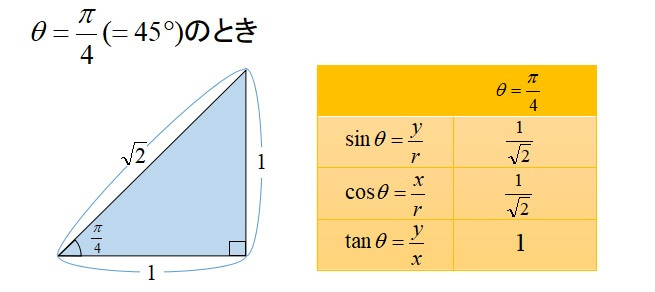
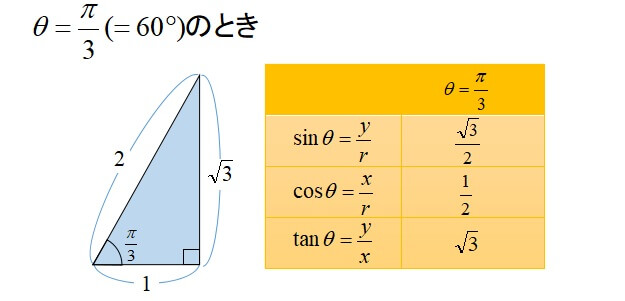
このように、斜辺の長さ、$x$座標、$y$座標が分かっていれば三角比を表すことができます。

また、$90^\circ$を超える場合も、三角形をイメージすることで三角比を求めることができます。

sin,cos,tanの覚え方を解説しました。
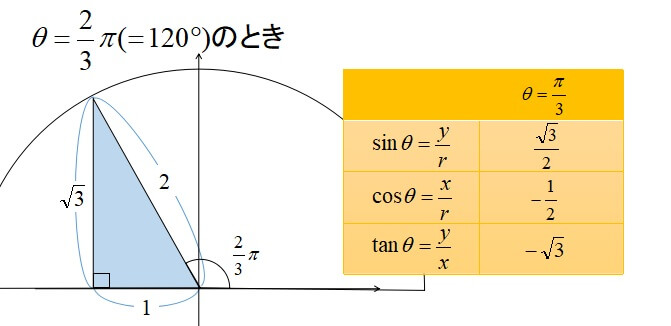
三角比の公式(sin,cos,tan)と覚え方
[st-card myclass=”” id=”2000″ label=”三角比” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

三角比の相互関係

三角比の相互関係は重要な公式です。

$\sin^{2} \theta+\cos^{2} \theta=1$

$\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}$

$\displaystyle 1+\tan ^{2} \theta=\frac{1}{\cos ^{2} \theta}$

[/st-mybox]

三角比の相互関係を用いれば、sin,cos,tanのどれか1つが分かれば、他のすべて求めることができます。

三角比の相互関係は必ず覚えよう！

⇒三角比の相互関係＜必ず覚えたい重要公式３つ！＞
[st-card myclass=”” id=”2095″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

三角比の拡張

$\sin(\theta+\pi)$など三角比の拡張公式をまとめました。

$-\theta$の公式

$-\theta$の公式は以下のようになります。

[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

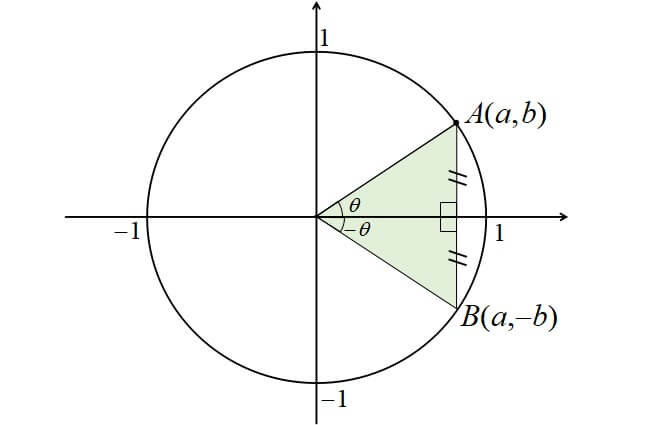
$\sin (-\theta)=-\sin \theta$
$\cos (-\theta)=\cos \theta$
$\tan (-\theta)=-\tan \theta$

[/st-mybox]

[st-cmemo myclass=”st-text-guide st-text-guide-attention” fontawesome=”fa-exclamation-circle” iconcolor=”#ef5350″ bgcolor=”#ffebee” color=”#000000″ bordercolor=”#ffcdd2″ borderwidth=”” iconsize=””]符号の入れ替わりに注意してください。[/st-cmemo]

$\displaystyle \theta+\frac{\pi}{2}$の公式

$\theta$に対して$\displaystyle \frac{\pi}{2}=90°$を加えると、以下のように変換することができます。

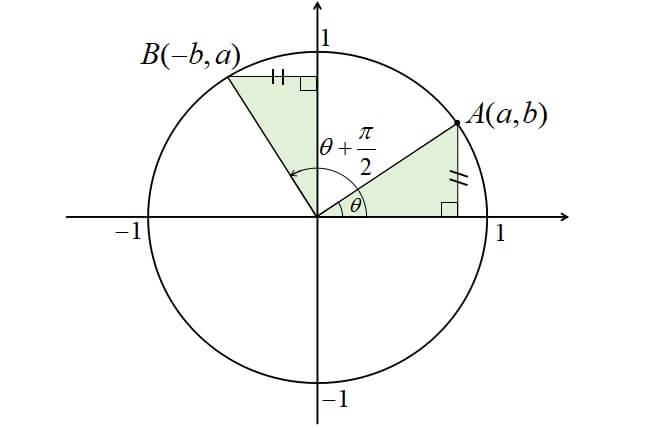
$\displaystyle \sin (\theta+\frac{\pi}{2})=\cos \theta$
$\displaystyle \cos (\theta+\frac{\pi}{2})=-\sin \theta $
$\displaystyle \tan (\theta+\frac{\pi}{2})=-\frac{1}{\tan \theta}$

[/st-mybox]

$\theta+\pi$の公式

$\theta$に対して$\pi=180°$を加えると、以下のように変換することができます。

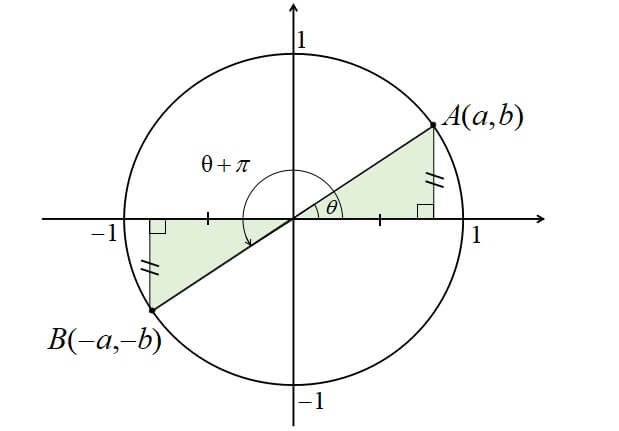
$\sin (\theta+\pi)=-\sin \theta $
$\cos (\theta+\pi)=-\cos \theta $
$\tan (\theta+\pi)=\tan \theta$

[/st-mybox]

詳しくは「θ＋π/2，θ+π三角関数の公式と導き方」
[st-card myclass=”” id=”2119″ label=”拡張公式” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

正弦定理

正弦定理は三角形に使う定理です。

各頂点A,B,Cとして、向かい合う辺をa,b,cとする。

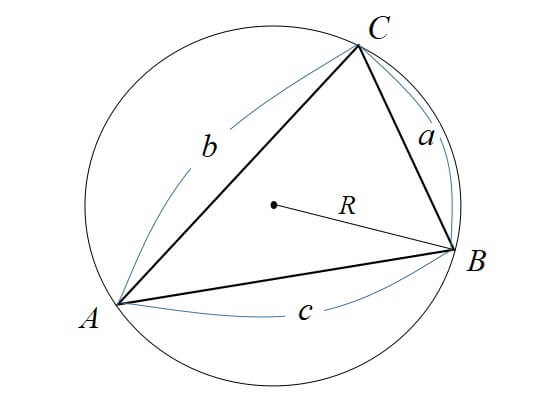
△ABCの外接円の半径をRとすると、次が成り立つ。

\[\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]

[/st-mybox]

正弦定理の使い方と証明はこちら
⇒正弦定理の公式と証明を5分でサクッと解説！
[st-card myclass=”” id=”2296″ label=”正弦定理” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

余弦定理

余弦定理も三角形に辺や角を求める定理です。

各頂点A,B,Cとして、向かい合う辺をa,b,cとする。

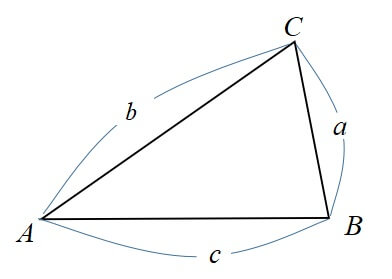
△ABCにおいて、次が成り立つ。

$a^{2}=b^{2}+c^{2}-2bc \cos \angle A$

$b^{2}=a^{2}+c^{2}-2ac \cos \angle B$

$c^{2}=a^{2}+b^{2}-2ab \cos \angle C$

[/st-mybox]

余弦定理の使い方と証明はこちら
⇒余弦定理をサクッと解説！
[st-card myclass=”” id=”2325″ label=”余弦定理” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

sinを使った面積公式

三角比を使って三角形の面積を求めることもできるんです。

sin（サイン）を用いた面積公式は三角形の2辺とその間の角が分かってるときに使うことができます。

$sinを用いた面積公式$

2辺の長さ a, b とその間の角 A の三角形の面積は
\[
\begin{aligned}
S &=\frac{1}{2} b c \sin A \\
&=\frac{1}{2} c a \sin B \\
&=\frac{1}{2} a b \sin C
\end{aligned}
\]

と表すことができる。

[/st-mybox]

sin（サイン）を用いる三角形の面積公式を解説！

[st-card myclass=”” id=”2452″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]

三角比の公式　まとめ

今回は三角比についての完全攻略記事としてまとめました。

三角比に関する記事を網羅的にまとめましたが、詳しいポイントは各単元の記事で解説しています。

そちらもぜひ参考にしてください。

[st-minihukidashi fontawesome=”fa-search” fontsize=”90″ fontweight=”bold” bgcolor=”#66BB6A” color=”#fff” margin=”0 0 0 0″]三角比[/st-minihukidashi]

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#E8F5E9″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]

三角比の公式
三角比の相互関係
三角比の拡張
正弦定理
余弦定理
sinを用いた三角形の面積

[/st-mybox]

三角比以外の単元についてもまとめ記事を出しています。

[st-mybox title=”まとめ記事” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

[/st-mybox]

教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。

それでは最後までご覧いただきありがとうございました。

みんなの努力が報われますように！

よかったらシェアしてね！

URLをコピーしました！

URLをコピーしました！

この記事を書いた人

ゆうや

当サイトの運営者。
指導歴8年目の数学講師。大学1年生から塾講師バイトを始め、これまで300名以上を指導。オンライン家庭教師のご依頼・お申し込みは、こちらの公式アカウントから承っております。詳しいプロフィール

三角比の重要単元まとめ！数学Ⅰ

三角比の重要公式一覧

三角比の基本公式

三角比の相互関係

正弦定理

余弦定理

\(\sin\)を用いた三角形の面積

三角比の公式

三角比の相互関係

三角比の拡張

\(-\theta\)の公式

\(\displaystyle \theta+\frac{\pi}{2}\)の公式

\(\theta+\pi\)の公式

正弦定理

余弦定理

sinを使った面積公式

三角比の公式　まとめ

この記事を書いた人

コメント

コメントするコメントをキャンセル

三角比の重要単元まとめ！数学Ⅰ

三角比の重要公式一覧

三角比の基本公式

三角比の相互関係

正弦定理

余弦定理

\(\sin\)を用いた三角形の面積

三角比の公式

三角比の相互関係

三角比の拡張

\(-\theta\)の公式

\(\displaystyle \theta+\frac{\pi}{2}\)の公式

\(\theta+\pi\)の公式

正弦定理

余弦定理

sinを使った面積公式

三角比の公式 まとめ

この記事を書いた人

関連記事

コメント

コメントする コメントをキャンセル

三角比の公式　まとめ

コメントするコメントをキャンセル