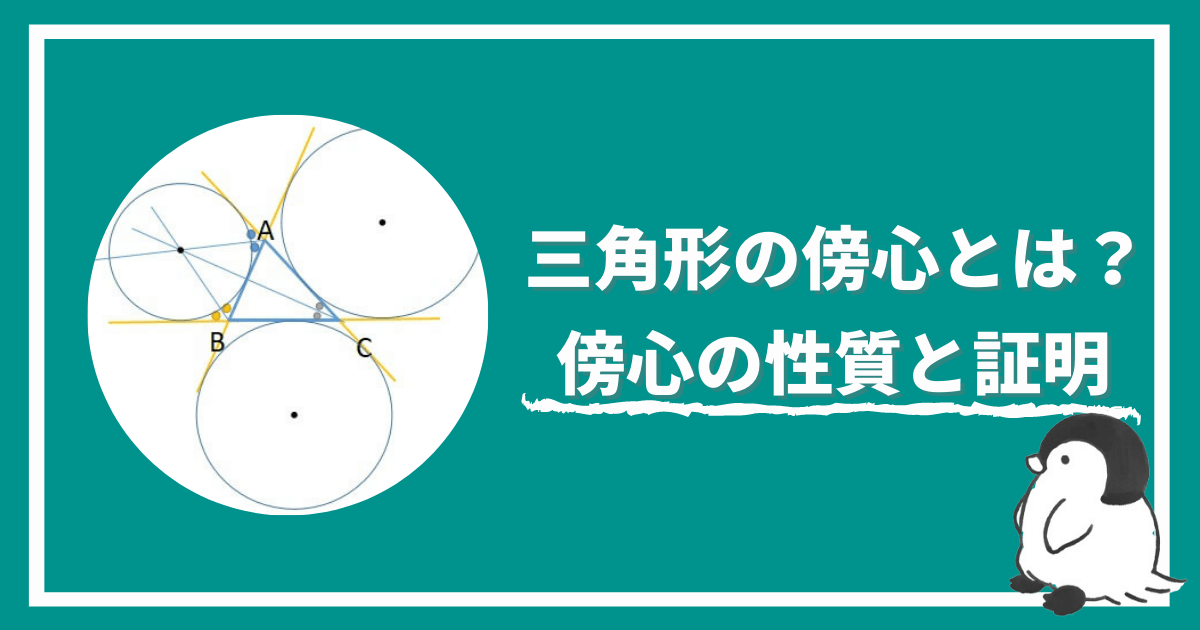
三角形には五心と呼ばれる5つの点が存在します。

今回は五心の中でも“傍心”についてまとめました。
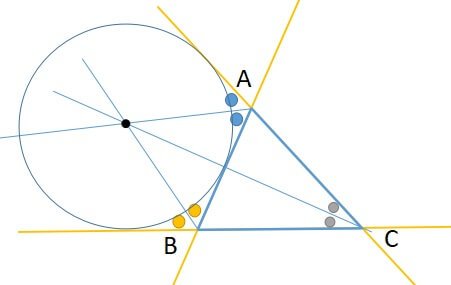
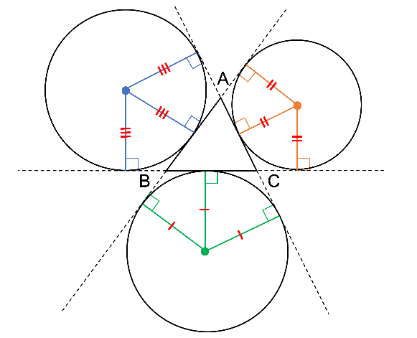
三角形の傍心とは、1つの角の二等分線と他の2つの外角の二等分線の交点を指します。
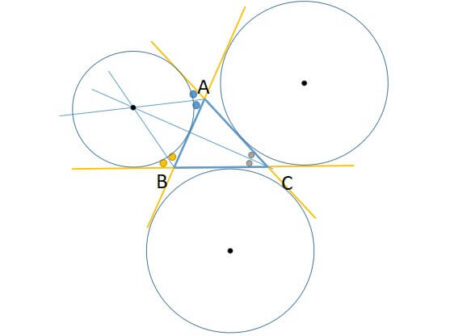
上図から分かるように、三角形には傍心が3つあります。
本記事では三角形の傍心について解説します。
傍心の定義や性質などが知りたい方は、ぜひ最後までご覧ください。
三角形の傍心とは

三角形の傍心とは、1つの角の二等分線と他の2つの外角の二等分線の交点を指します。
文字ではピンとこないと思うので、詳しく解説していきましょう。
動画で解説が見たい方は「とある男が授業をしてみた」の葉一さんが分かりやすく解説しています。
下の図のように三角形の3辺の延長線を描きます。
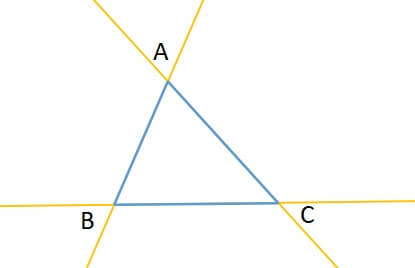
三角形の外角の二等分線と向かい合う頂点の二等分線が1点で交わります。
この交点が三角形の傍心です。
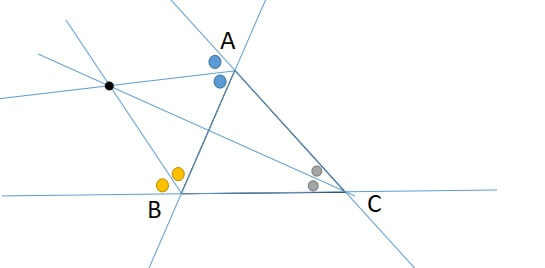
外角の二等分線2本と向かい合う頂点の二等分線がかならず1点で交わることの証明はこちら。
⇒傍心の存在証明はこちらから
傍心は1つの三角形に対して3点存在します。

三角形の傍心と内心の関係
三角形の内心は角の二等分線の交点なので三角形の内側に存在します。
それに対して、傍心は外角の二等分線の交点なので三角形の外側に存在します。
内心と傍心ではまったく違う点に見えますが、内心と同じような性質を持っています。
内心と傍心のどちらも“角の2等分線の交点”なので似たような性質を持ちます。
その性質のひとつを紹介します。
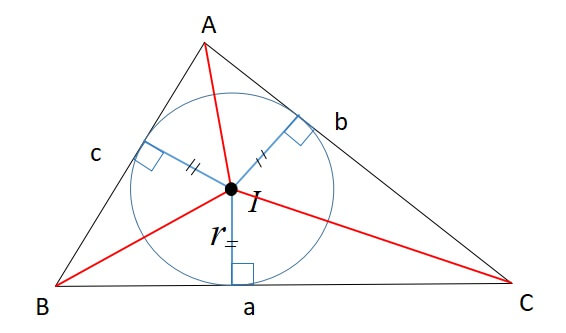
内心は三角形の内接円の中心の点です。
三角形の面積を\(S\)、内接円の半径を\(r\)とすると
\[S=\displaystyle \frac {1}{2} r(a+b+c)\]
が成り立ちます。
それに対して、傍心を中心として周りに接する半径\(r_{A}\)の円を描きます。
この円を傍接円といいます。
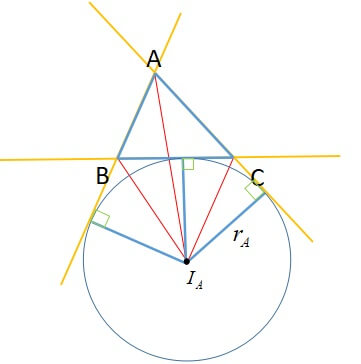
このとき、
\[△ABC=-△I_{A}BC+△I_{A} C A+△I_{A}AB\]
となり、
\[\displaystyle S=\frac{1}{2} r_{A}(-a+b+c)\]
が成り立ちます。
傍心の存在証明
三角形の傍心が存在することの証明をします。
「外角の二等分線と対角の二等分線が1点で交わること」がすべての三角形でいえるのかを確かめましょう。
長くなってしまったので証明が気になる方は下をクリックしてください。
傍心の性質

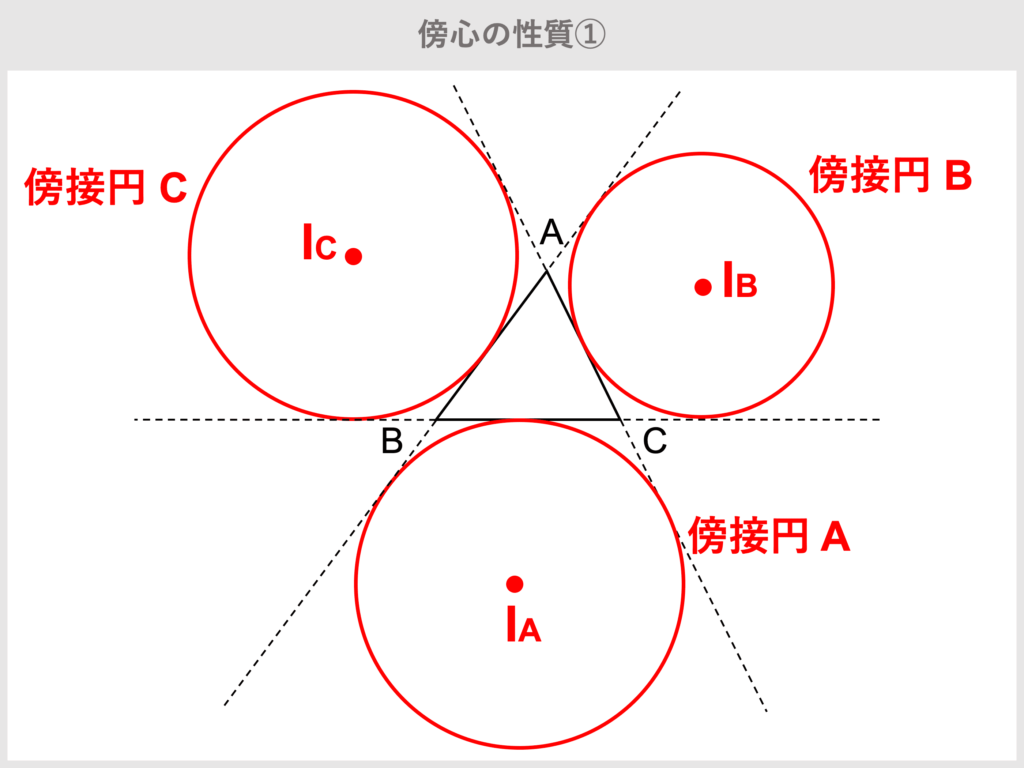
1つの三角形に対して、傍心と傍接円は3個存在します。
傍心は内心と似た性質をもっています。
そこで傍心・内心に関する重要な性質を 4つ紹介します。
【性質①】傍心は傍接円の中心である
傍心は傍接円の中心です。
【性質②】傍心からの垂線の長さと傍接円の半径は等しい
△ABCにおいて、傍心からの各辺にひいた垂線の長さと傍接円の半径は等しい。
【性質③】△ABCの内心Iは、△ABCの傍心を頂点とする三角形の垂心
3つの傍心を\(I_{A},I_{B},I_{C}\)とすると、\(\triangle ABC\)の内心Iは\(\triangle I_{A}I_{B}I_{C}\)の垂心である。
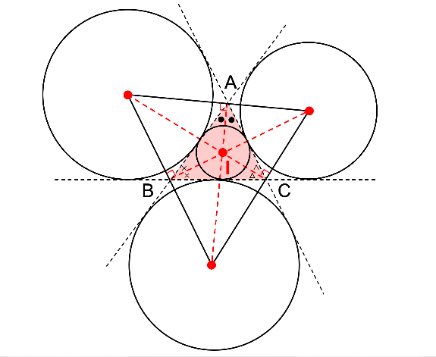
【性質④】傍心\(I_{A}\)は直線\(AI\)上に存在する
傍心も内心も角の二等分線の交点で定義される点なので、傍心\(I_{A}\)は直線\(AI\)上に存在する

三角形の傍心の書き方
三角形の傍心の書き方を図を用いて解説します。
必要なのは、三角形、筆記用具、コンパスです。

手順は簡単です。
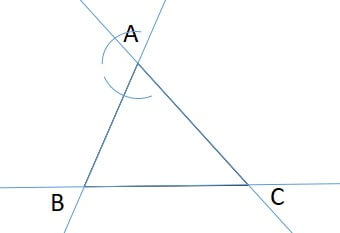
三角形のどこかの頂点にコンパスの針を置いて弧を描きます。
そのとき辺と辺の延長線の2か所で交わります。
次に、どちらかの交点にコンパスの針を置きなおし、弧を描きます。
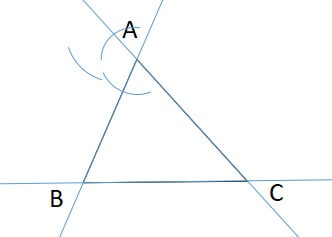
これができたら、もう片方の交点にコンパスを置きなおし、もう一度弧を描きます。
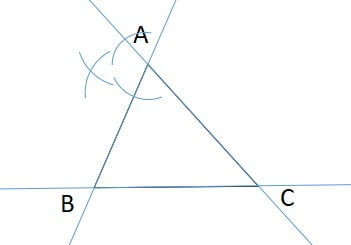
2つの弧の交点と、初めにコンパスを置いた頂点を結んだものが外角の二等分線です。
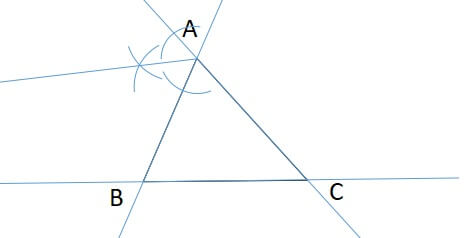
別の外角でも同様のことをします。
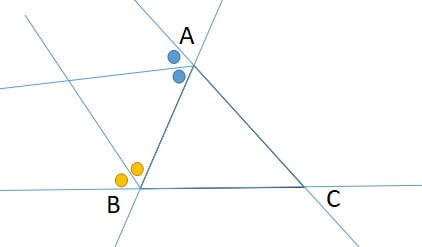
2つの外角の二等分線が交わったところが傍心です。
傍心の位置ベクトル
3点の傍心\(I_{a},I_{b},I_{c}\)の位置ベクトルは以下のように表されます。
傍心の位置ベクトル《証明》
辺 \(BC\) に関して頂点\(A\)と反討側にある傍心\(I_{a}\left(\vec{i_{a}}\right)\)について証明します。
(他の傍心の場合も同樣)
\(I_{a}\)は角\(A\)の2等分線上にあるから
\[\displaystyle \overrightarrow{AI_{a}}=s\left(\frac{1}{c} \overrightarrow{\mathrm{AB}}+\frac{1}{b} \overrightarrow{\mathrm{AC}}\right)(0<s) \]
と表せる。
一方で、
\(\mathrm{I}_{a}\)は角\(C\)の外角の2等分線上の点でもあるから
\begin{eqnarray}
\displaystyle \overrightarrow{AI_{a}}&=&\overrightarrow{AC}+\overrightarrow{CI_{a}}\\
\displaystyle &=&\overrightarrow{AC}+t\left(\frac{1}{a} \overrightarrow{CB}+\frac{1}{b} \overrightarrow{AC}\right) \quad(t>0)\\
\displaystyle &=&\overrightarrow{AC}+t\left\{\frac{1}{a}(\overrightarrow{AB}-\overrightarrow{AC})+\frac{1}{b} \overrightarrow{AC}\right\}\\
\displaystyle &=&\frac{t}{a} \overrightarrow{AB}+\left(1-\frac{t}{a}+\frac{t}{b}\right) \overrightarrow{AC}
\end{eqnarray}
と表すこともできる。
\(\overrightarrow{\mathrm{AB}} \neq \overrightarrow{0}, \overrightarrow{\mathrm{AC}} \neq \overrightarrow{0} \)かつ\(\overrightarrow{\mathrm{AB}}\)と\(\overrightarrow{\mathrm{AC}}\)は平行でないので,
\begin{eqnarray}
\displaystyle \frac{s}{c}&=&\frac{t}{a}\\
\displaystyle \frac{s}{b}&=&1-\frac{t}{a}+\frac{t}{b}
\end{eqnarray}
を得る。
これを解いて、
\[\displaystyle s=\frac{b c}{-a+b+c}, \quad t=\frac{a b}{-a+b+c}\]
よって、
\begin{eqnarray}
\displaystyle \overrightarrow{\mathrm{AI_{a}}}&=&\frac{b}{-a+b+c} \overrightarrow{\mathrm{AB}}+\frac{c}{-a+b+c} \overrightarrow{\mathrm{AC}}\\
\displaystyle &=&\frac{b}{-a+b+c}(\vec{b}-\vec{a})+\frac{c}{-a+b+c}(\vec{c}-\vec{a})\\
\displaystyle &=&\frac{-b-c}{-a+b+c} \vec{a}+\frac{b}{-a+b+c} \vec{b}+\frac{c}{-a+b+c} \vec{c}
\end{eqnarray}
したがって、
\begin{eqnarray}
\displaystyle \vec{i_{a}}&=&\vec{a}+\overrightarrow{\mathrm{AI_{a}}}\\
\displaystyle &=&\frac{-a \vec{a}+b \vec{b}+c \vec{c}}{-a+b+c}
\end{eqnarray}
よって証明終了
三角形の傍心 まとめ
今回は傍心の定義や性質をまとめました。

⇒傍心の性質についてはこちら
傍心はなかなか問題に出てきませんが、知っておくと周りと差がつきます。
傍心は五心のなかではマイナーな点です。
「内心」や「外心」は重要な点なので必ず確認しておきましょう。
傍心以外の五心についてはこちらの記事でまとめました