三角形の垂心がいまいちな方は必見です!
今回は垂心に関するこんな悩みを個別指導歴10年の数学講師が解決します。
 高校生
高校生三角形の垂心がよく分からなくて…

三角形には五心と呼ばれる5つの点があります。

三角形の垂心とは、各頂点から対辺に向かって垂線を引いた交点を指します。
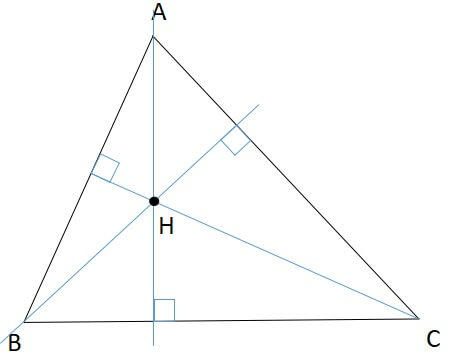
本記事では三角形の垂心の定義や性質について解説します。
三角形の垂心に関する悩みをすべて解決できるように解説したので、ぜひ最後まで見ていってください。
三角形の垂心とは?
三角形の垂心とは、三角形の各頂点から対辺に向かってひいた垂線の交点を指します。

各頂点から向かい合う辺に下した垂線の交点
以下のように三角形\(ABC\)があります。
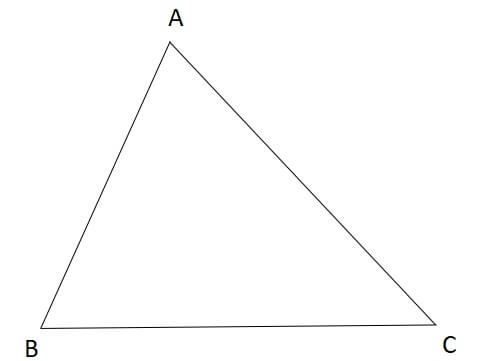
三角形の各頂点から対辺に向かって垂線を引きます。

すると3本の垂線が1点で交わり、その点を三角形の垂心とよびます。
 高校生
高校生垂線の交点だから垂心ですね!
 シータ
シータ垂心の定義は分かりやすくていいね!
垂線が1点で交わることの証明
垂線が1点で交わることの証明は、「2本の垂線の交点を3本目の垂線も通過する」ことを証明します。
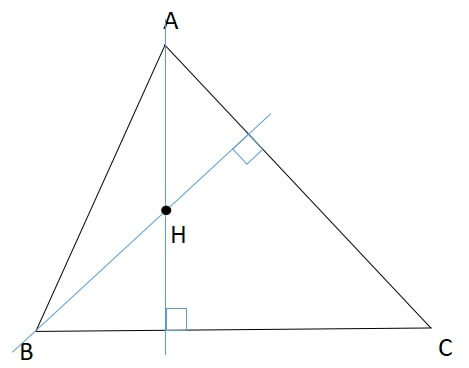
まずは2本の垂線があり、その交点を交点Hとしましょう。
そのあと交点Hを通過するように線分CDを引いたものが下図です。
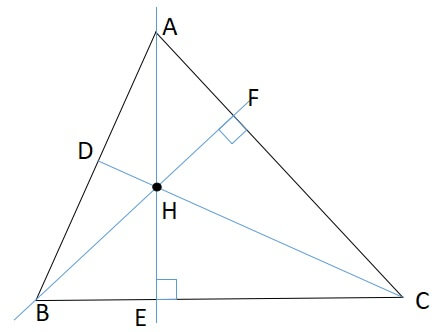
この段階ではまだ\(\angle CDA\)が垂直とは分かりません。
そこで、線分CDが垂直であることを証明できれば、3本の垂線が1点で交わることを示せます。
\(\angle CFH,\angle CEH\)はともに直角なので、 C, F, H, E の4点は、CHを直径とする円周上にあります。
このことから、円周角の定理より
\(\angle HCF=\angle HEF\)が言えます。(下図を参考にしてください)
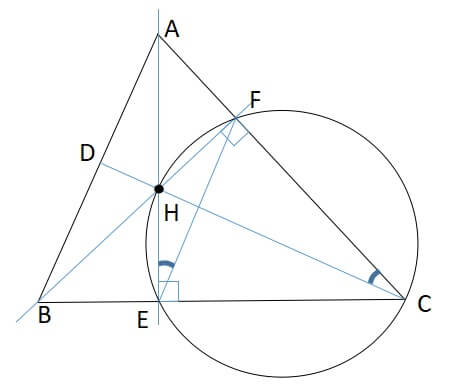
また、\(\angle AEB,\angle AFB\)もともに直角なので、 A, B, E, F の4点は、ABを直径とする円周上にあります。
このことから、\(\angle AEF=\angle ABF\)であることがわかります。
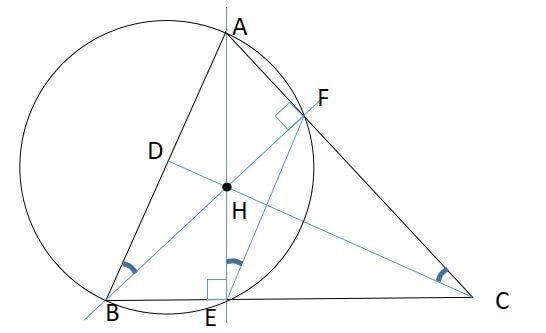
よって、
2つを合わせると、\(\angle ACD=∠ABF\)がわかります。
\begin{eqnarray}
\angle \mathrm{ADC} &=&180^{\circ}-\angle \mathrm{DAC}-\angle \mathrm{ACD} \\
&=&180^{\circ}-\angle \mathrm{BAF}-\angle \mathrm{ABF} \\
&=&\angle \mathrm{AFB} \\
&=&90^{\circ}
\end{eqnarray}
したがって、3本の垂線が1点で交わることが証明されました。

垂心が持つ性質
三角形の垂心には2つの性質があります。
まず性質を紹介してから証明をします。
1:四角形ADHF,BEHD,CFHEは円に内接する四角形である
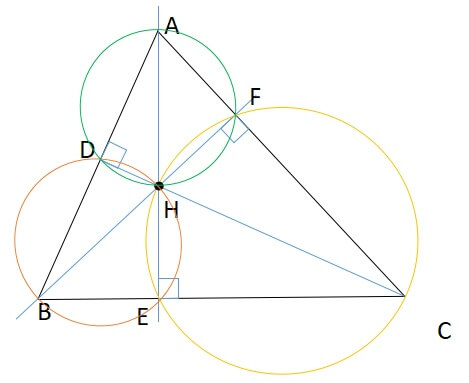
2:\(AH=2R\cos A\)
Rは三角形ABCの外接円の半径を表します。
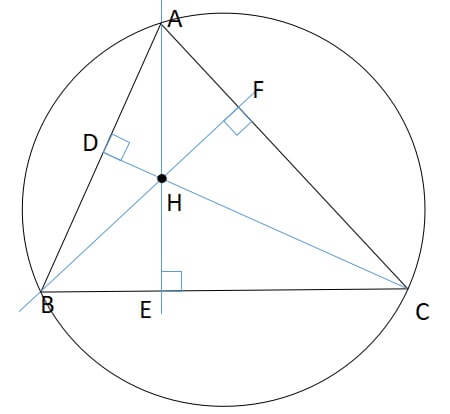
垂心の性質《証明》
三角形の垂心がもつ性質の証明をします。
まずは「四角形ADHF,BEHD,CFHEは円に内接する四角形である」を証明していきます。
これには、中学3年生で習った円周角の定理を使うと理解が早いです。
四角形CFHEに注目すると、\(\angle CFH=90^\circ\),\(\angle CEH=90^\circ\)
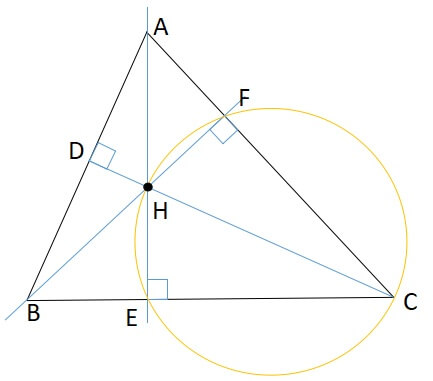
したがって、円周角の定理の逆を用いて、CHを直径とする円が見えてきます。
他の四角形でも同様の証明ができます。
つぎに垂心の性質2「\(AH=2R\cos A\)」の証明をします。
これは三角関数の正弦定理を用いて証明します。
三角形ABCの外接円の半径を\(R\)とします。

\(AH=\displaystyle \frac{AF}{\cos \angle CAE}\)
\(AF=AB\cos A\)
\(\cos \angle CAE=\sin(90^\circ-\angle CAE)=\sin \angle ACE\)
なので、
\[\displaystyle \frac{AF}{\cos \angle CAE}=\displaystyle \frac{AB\cos A}{\sin \angle ACE}\]
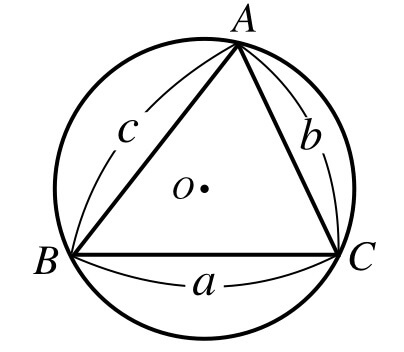
三角形ABCの外接円の半径をRとしたとき、
\[\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
正弦定理について知りたい方は「正弦定理の公式と証明」をご覧ください。
正弦定理より
\[\displaystyle \frac{AB\cos A}{\sin \angle ACE}=2R\cos A\]
したがって、
\[AH=2R\cos A\]
証明終了。
三角形の垂心の見つけ方

三角形の垂心は作図だけでなく、座標や位置ベクトルを求めることもあります。
垂心の作図
超基本ですが実際に垂線を引いて垂線を見つけます。
必要なのは、三角形、筆記用具、コンパスです。

どこかの頂点にコンパスの針を刺して弧を描きます。
このときコンパスが描く弧が向かい合う辺と交わるようにしてください。
弧が描けたら、2つの交点を交点ア、イとしましょう。
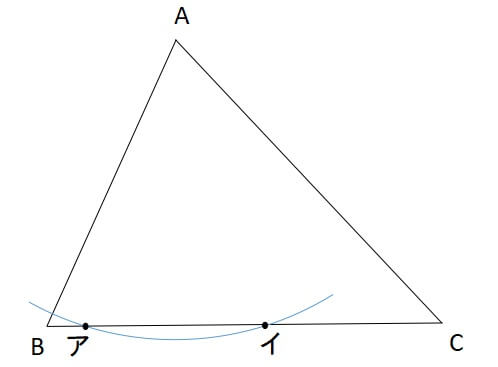
針の先を交点アに置き換えて、弧を描きます。
交点イでも同じことをしましょう。
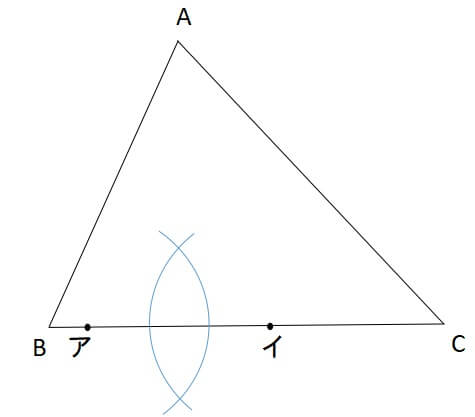
すると、2つの弧が交わります。
交わった弧の交点と頂点を結ぶように直線を引くと、これが垂直です。
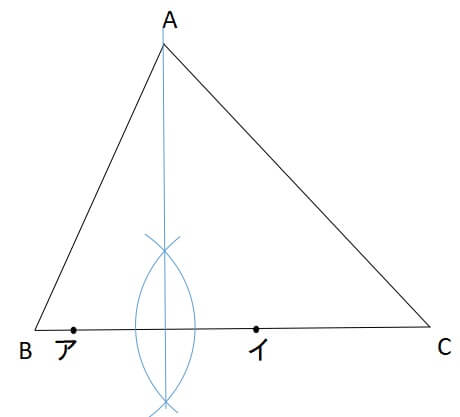
同様に他の頂点からも垂線を引いて、交わった点が垂心です。
垂心の座標
垂心の座標公式があることを知っていますか?
下の図のような1辺が\(y\)軸に平行な三角形があります。

三角形の各頂点の座標を\(A(a_{x},a_{y}),B(0,0),C(c_{x},c_{y})\)とする。
このとき垂心Hの座標は
\[\displaystyle H(a_{x},\frac{-a_{x}^{2}+a_{x}c_{x}+a_{y}c_{y}}{a_{y}})\]
ただし、これは三角形の1辺が\(y\)軸に平行かつ1つの頂点を原点としたときの座標なので注意してください。
垂心の位置ベクトル
三角形ABCの垂心をHとすると、垂心の位置ベクトルは以下のように表すことができます。
\[\displaystyle \vec{h} =\frac{\tan A \vec{a} + \tan B \vec{b} +\tan C \vec{c}}{\tan A +\tan B +\tan C}\]
これには以下のような三角形と位置ベクトルの性質が関係しています。
三角形ABCについて、BC上の点P、CA上の点Q、AB上の点Rに対して
AR : RB = y : x
BP : PC = z : y
CQ : QA = x : z
のとき、線分AP、BQ、CRはチェバの定理により一点Hで交わり、Hの位置ベクトルは
\(\displaystyle \vec{h} =\frac{x\vec{a} + y\vec{b} +z\vec{c}}{x+y +z}\)
で表される。
この性質を活用して垂心の位置ベクトルを求めます。

上の図のように三角形ABCの垂心をH、AHとBCの交点をE、BHとCAの交点をF、CHとABの交点をDとします。
三角形AEBと三角形AECは直角三角形なので、
\[AE = BE \tan B = EC \tan C\]
となります。
これを比例式としてみると
\[BE : EC = \tanC : \tanB\]
です。
同様に
\(AD : DB = \tan B : \tan A\)
\(CF : FA = \tan A : \tan C\)
ここで先ほど解説した位置ベクトルの性質より垂心の位置ベクトルは
\[\displaystyle \vec{h} =\frac{\tan A \vec{a} + \tan B \vec{b} +\tan C \vec{c}}{\tan A +\tan B +\tan C}\]
となります。
垂心の他にも「内心」や「重心」など五心には重要な点があります。
三角形の垂心 まとめ
今回は五心の中から「垂心」をピックアップして解説しました。

三角形の垂心とは、各頂点から対辺に向かってひいた垂線の交点を指します。
垂心の性質
- 四角形ADHF,BEHD,CFHEは円に内接する四角形である
- \(AH=2R\cos A\) (Rは三角形ABCの外接円の半径)
垂心の性質は知っているものとして問題が出されます。
垂線が1点で交わることの証明には他の方法もあります。
ただ、今回紹介した証明が1番わかりやすいと感じたので確認しておきましょう。
垂心の他にも「内心」や「重心」など五心には重要な点があります。

