「ベクトル方程式ってなに?」
「ベクトル方程式はどう使うの?」
今回は数学Bのベクトルから「ベクトル方程式」に関するこんな悩みを解決します。
ベクトル方程式とは、ベクトルを用いた式で直線や円の概形を示すものです。
①ある点aを通る直線
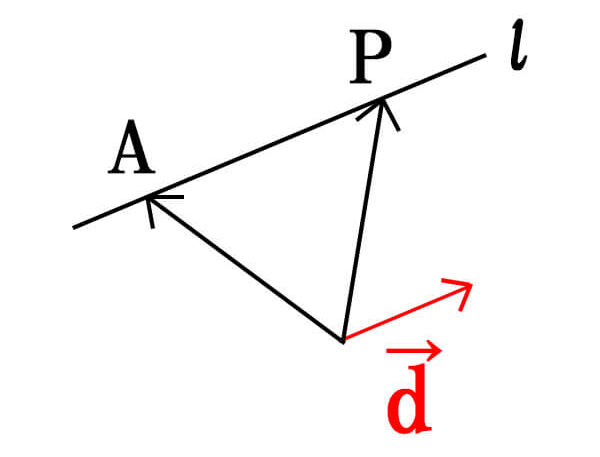
点Aを通り、傾きが\(\vec{d}(\vec{d}\neq0)\)に平行な、直線\(l\)上の点Pは、
\[\vec{OP}=\vec{OA}+t\vec{d} (tは実数)\]
②異なる2点を通る直線
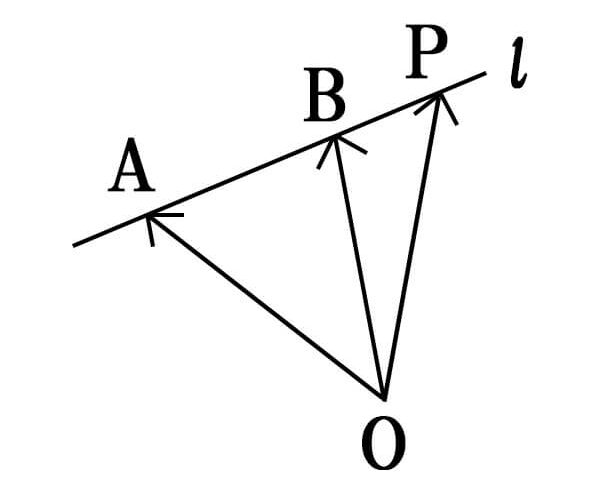
2つの点、A,Bを通る直線l上の点Pは、
\[\vec{OP}=(1-t)\vec{OA}+t\vec{OB} (tは実数)\]
③中心\(a\),半径\(r\)の円
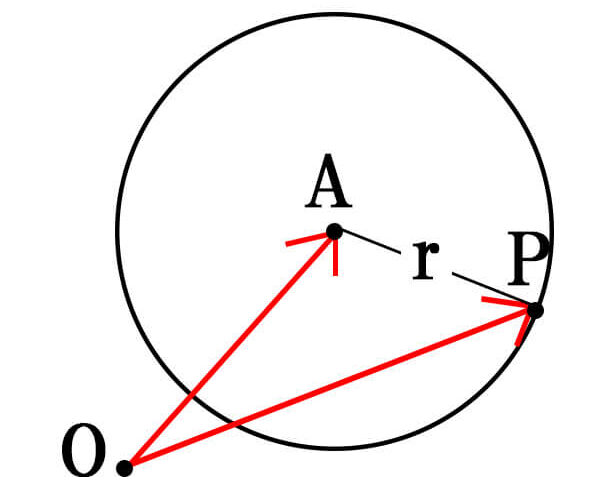
点Aを中心とし、半径rの円上にある点Pのベクトル方程式は、
\begin{eqnarray}
|\vec{AP}|&=&r\\
\Leftrightarrow |\vec{OP}-\vec{OA}|&=&r
\end{eqnarray}
④線分\(AB\)を直径とする円
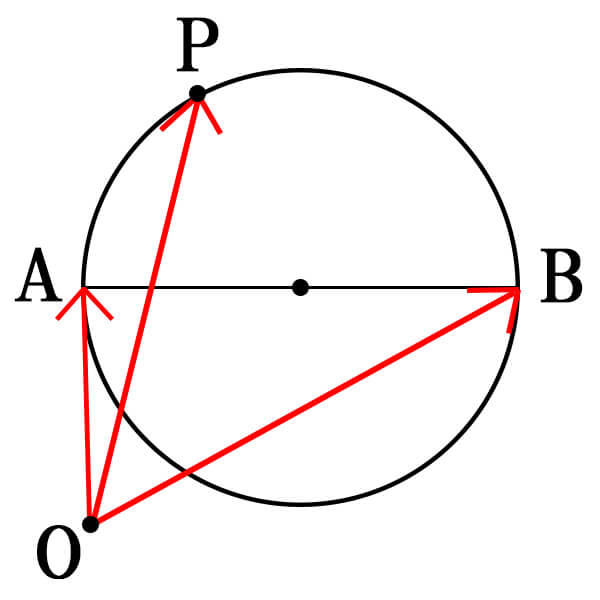
線分ABを直径とする円上にある点Pのベクトル方程式は、
\begin{eqnarray}
\vec{AP} \cdot \vec{BP}&=&0\\
\vec{OP}-\vec{OA}) \cdot (\vec{OP}-\vec{OB})&=&0
\end{eqnarray}
⑤平面ABC
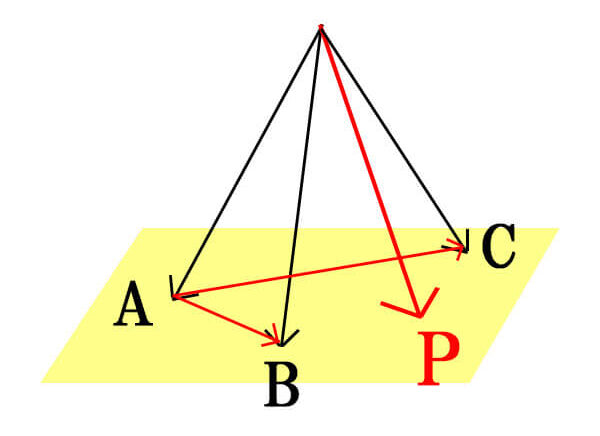
平面ABC上の点Pのベクトル方程式は、
\[\vec{OP}=(1-s-t)\vec{OA}+s\vec{OB}+t\vec{OC} (s,tは実数)\]
座標平面において、直線のベクトル、円のベクトル、平面上の点を表すベクトルはそれぞれベクトルを使った式で表すことができます。
本記事ではベクトルの方程式について解説していきます!
ベクトルに苦手意識がある方はぜひ最後までご覧ください。
それではベクトルのなす角について解説していきましょう。
ベクトル方程式とは?
ベクトル方程式とは「ある条件を満たす点を、ベクトルを使って表現した式」のことを指します。
例えば、以下の式は直線を表しています。

\[\vec{OP}=\vec{OA}+t\vec{d} (tは実数)\]
このようにベクトルを上手く使い、直線や円、平面を1つの式で表したものがベクトル方程式です。
ベクトル方程式一覧
ベクトル方程式には「直線」「円」「平面」を表すものがあります。
詳しくは本記事の後半で解説しますが、まずはサクッとベクトル方程式の公式を見ていきましょう。
直線のベクトル方程式
まずは直線のベクトル方程式について紹介します。
直線のベクトル方程式には2パターンありますので使い分けられるようになりましょう。
①ある点を通る場合

点Aを通り、傾きが\(\vec{d}(\vec{d}\neq0)\)に平行な、直線\(l\)上の点Pは、
\[\vec{OP}=\vec{OA}+t\vec{d} (tは実数)\]
と表すことができる。
②異なる2点を通る場合

2つの点、A,Bを通る直線l上の点Pは、
\[\vec{OP}=(1-t)\vec{OA}+t\vec{OB} (tは実数)\]
と表すことができる。
円のベクトル方程式
次は、円のベクトル方程式について学習します。
こちらも2パターンありますので、まずは見てみましょう。
①中心a,半径rの場合

点Aを中心とし、半径rの円上にある点Pのベクトル方程式は、
\begin{eqnarray}
|\vec{AP}|&=&r\\
\Leftrightarrow |\vec{OP}-\vec{OA}|&=&r
\end{eqnarray}
②線分ABを直径とする場合

線分ABを直径とする円上にある点Pのベクトル方程式は、
\begin{eqnarray}
\vec{AP} \cdot \vec{BP}&=&0\\
\vec{OP}-\vec{OA}) \cdot (\vec{OP}-\vec{OB})&=&0
\end{eqnarray}
平面のベクトル方程式

平面ABC上の点Pのベクトル方程式は、
\[\vec{OP}=(1-s-t)\vec{OA}+s\vec{OB}+t\vec{OC} (s,tは実数)\]
直線のベクトル方程式
この章では直線のベクトル方程式についてより詳しく学習します。
図を用いながら分かりやすく解説していくので、一緒に頑張りましょう!
ある点aを通る場合

点Aを通り、傾きが\(\vec{d}(\vec{d}\neq0)\)に平行な、直線\(l\)上の点Pは
\[\vec{OP}=\vec{OA}+t\vec{d} (tは実数)\]
と表すことができる。
少し詳しく解説していきます。
まず、\(\vec{OP}\)ですが、ベクトルの性質から、\(\vec{OP}=\vec{OA}+\vec{AP}\)と表すことができます。
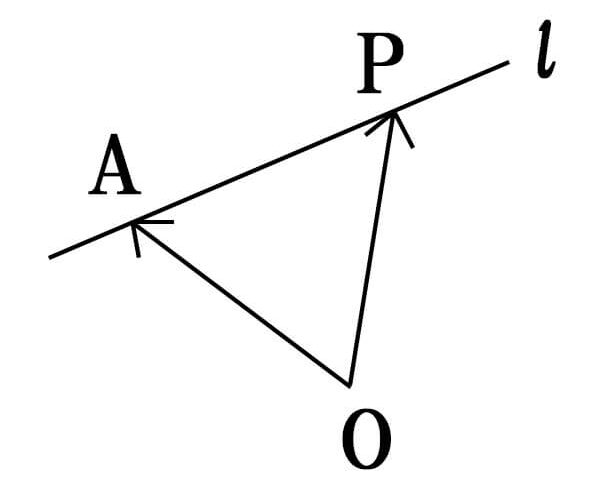
このとき、\(\vec{AP}\)と\(\vec{d}\)は平行であるため、ベクトルの平行条件から
\(\vec{AP}=t\vec{d}\)(tは実数)になります。
ここで先ほどの式、\(\vec{OP}=\vec{OA}+\vec{AP}\)に、この\(\vec{AP}=t\vec{d}\)を代入すると、
\[\vec{OP}=\vec{OA}+t\vec{d}\]
という式が成り立ちます。
つまり、ある点に対して、ベクトルを「傾き」として考えることで式が決定されるということですね。

異なる2点a,bを通る場合

2つの点、A,Bを通る直線\(l\)上の点Pは、
\[\vec{OP}=(1-t)\vec{OA}+t\vec{OB} (tは実数)\]
と表すことができる。
こちらも詳しく解説していきます。
図を見ると分かりやすいですが、\(\vec{OP}=\vec{OA}+t\vec{AB}\)と表すことができます。
\(\vec{AB}=\vec{OB}-\vec{OA}\)であるから、これを代入すると
\begin{eqnarray}
\vec{OP}&=&\vec{OA}+t\vec{AB}\\
\vec{OP}&=&\vec{OA}+t(\vec{OB}-\vec{OA})\\
\vec{OP}&=&(1-t)\vec{OA}+t\vec{OB}
\end{eqnarray}
となります。
円のベクトル方程式
次は、円のベクトル方程式について学習します。
こちらも丁寧に解説していきますね!
中心a,半径rの場合

点Aを中心とし、半径rの円上にある点Pに対して、次が成り立つ。
\begin{eqnarray}
|\vec{AP}|&=&r\\
\Leftrightarrow |\vec{OP}-\vec{OA}|&=&r
\end{eqnarray}
図を見ると分かりやすいですが、\(|\vec{AP}|\)は半径\(r\)と等しくなります。
これと、\(|\vec{AP}|=|\vec{OP}-\vec{OA}|\)より、上が成り立つことが分かります。
さらに、円の方程式との関連が分かるように成分表示でこの式を表してみましょう。
\(\vec{OP}=(x,y),\vec{OA}=(a_{1,}a_{2})\)とします。
\(\vec{OP}-\vec{OA}=(x-a_{1,}y-a_{2})\)となり、
\begin{eqnarray}
{|\vec{OP}-\vec{OA}|}^{2}&=&r^{2}\\
{(x-a_{1})}^{2}+{(y-a_{2})}^{2}&=&r^{2}
\end{eqnarray}
こう見ると、中心と半径が与えられた円の方程式との関連性が見えますね。
線分ABを直径とする場合

線分ABを直径とする円上にある点Pのベクトル方程式は、
\[(\vec{OP}-\vec{OA})\cdot(\vec{OP}-\vec{OB})=0\]
円周上の点と直径の関係から、\(AP\bot BP\)となる。
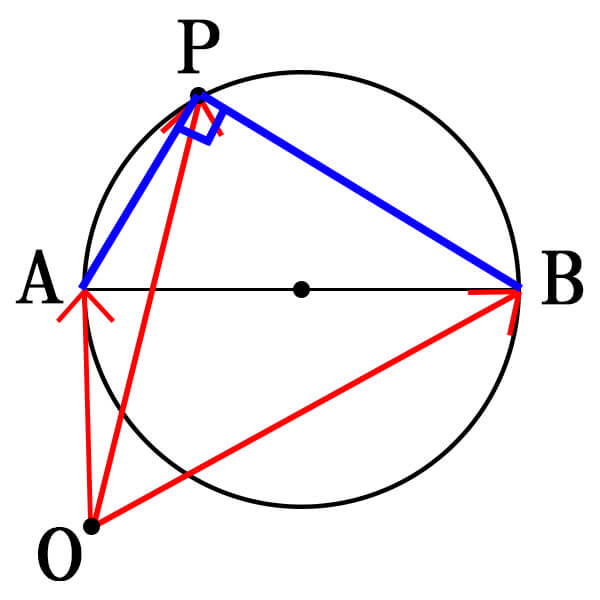
ここで、ベクトルの垂直条件から、
\begin{eqnarray}
\vec{AP}\cdot\vec{BP}&=&0\\
\Leftrightarrow (\vec{OP}-\vec{OA})\cdot(\vec{OP}-\vec{OB})&=&0
\end{eqnarray}
が成り立つことが分かる。
平面のベクトル方程式

平面ABC上にある点Pのベクトル方程式は、
\[\vec{OP}=(1-s-t)\vec{OA}+s\vec{OB}+t\vec{OC} (s,tは実数)\]
\(\vec{OA},\vec{OB},\vec{OC}\)の係数の和が1になることがポイントです。
こちらも図を用いながら説明していきます。
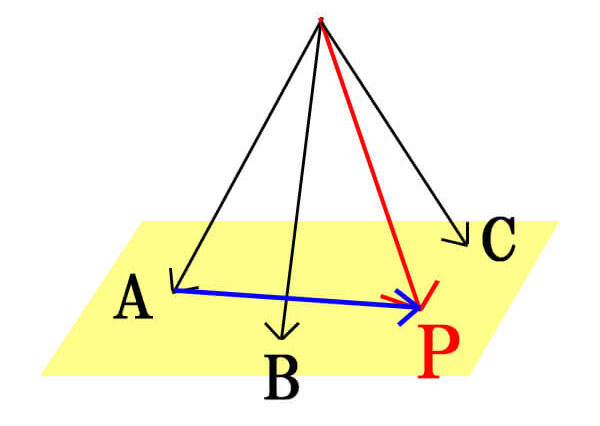
まず、\(\vec{OP}=\vec{OA}+\vec{AP}\)と表せることが分かります。
次に、\(\vec{AP}\)ですが、点Pが平面ABC上にあるので、同じ平面ABC上にある2つのベクトルの和で表すことができます。
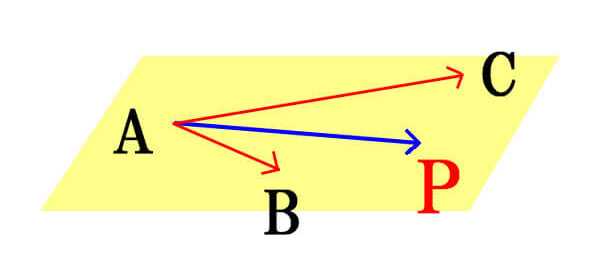
平面ABC上にある、\(\vec{AB},\vec{AC}\)を使って、
\[\vec{AP}=s\vec{AB}+t\vec{AC}(s,tは実数)\]
と表せました。
これを先ほどの\(\vec{OP}\)の式に代入すると、
\[\vec{OP}=\vec{OA}+s\vec{AB}+t\vec{AC}(s,tは実数)\]
ここからもう少し変形して、
\(\vec{AB},\vec{AC}\)を\(\vec{OA},\vec{OB},\vec{OC}\)を使って表すと、
\begin{eqnarray}
\vec{OP}&=&\vec{OA}+s\vec{AB}+t\vec{AC}(s,tは実数)\\
\vec{OP}&=&\vec{OA}+s(\vec{OB}-\vec{OA})+t(\vec{OC}-\vec{OA})\\
\vec{OP}&=&(1-s-t)\vec{OA}+s\vec{OB}+t\vec{OC}
\end{eqnarray}
ベクトル方程式《練習問題》
直線/円/平面のベクトル方程式を学習したところで、べクトル方程式の問題を3問用意しました。
今まで学習してきたことをもとに、一緒に解いてみましょう。
ベクトル方程式《問題①》
点A(2,1)を通り、\(\vec{d}=(3,4)\)に平行な直線\(l\)の方程式を\(x\)と\(y\)を用いて表してください。
ベクトルの情報を頼りに、直線の式を求めていきましょう。
解答をチェックする
まず、\(l\)上の点を1つ取り、その点を点P\((x,y)\)とする。
このとき、
\[\vec{OP}=\vec{OA}+t\vec{d}(tは変数)\]
と表せる。
これが直線のベクトル方程式でしたね!
この式を成分表示にすると、
\[(x,y)=(2,1)+t(3,4)\]
よって、
\begin{eqnarray}
x&=&2+3t \cdots ①\\
y&=&1+4t \cdots ②
\end{eqnarray}
①②を\(t\)についての式に変形すると、
\begin{eqnarray}
\displaystyle t=\frac{1}{3}x-\frac{2}{3} \cdots ③\\
\displaystyle t=\frac{1}{4}y-\frac{1}{4} \cdots ④
\end{eqnarray}
③④より、
\begin{eqnarray}
\displaystyle \frac{1}{3}x-\frac{2}{3}&=&\frac{1}{4}y-\frac{1}{4}\\
\displaystyle y&=&\frac{4}{3}x-\frac{5}{3}
\end{eqnarray}
したがって求める直線の方程式は\(\displaystyle y=\frac{4}{3}x-\frac{5}{3}\)
ベクトル方程式《問題②》
円の中心がAで、原点Oを通る円のベクトル方程式を求めてください。
次は円のベクトル方程式を求めていきましょう。
解答をチェックする
まず、情報を整理します。
中心がAで原点Oを通る円は以下の図のようになります。
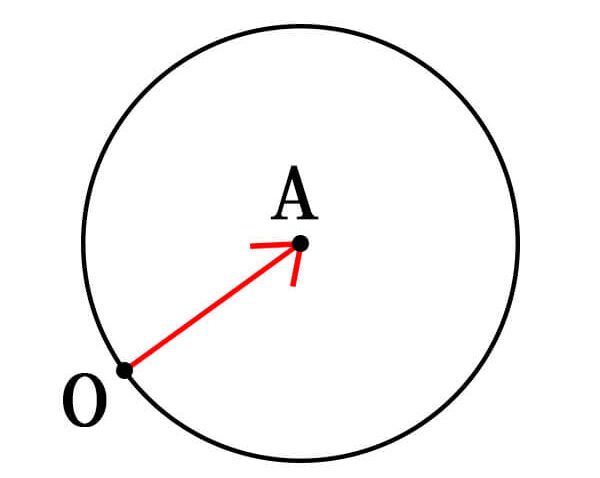
このとき、半径\(r\)は\(r=AO=|\vec{AO}|=|\vec{OA}|\)である。
円のベクトル方程式は、\(|\vec{OP}-\vec{OA}|=r\)で表されることから、
\[|\vec{OP}-\vec{OA}|=|\vec{OA}|\]
ベクトル方程式《問題③》
3点\(A(4,1,3),B(-1,0,1),C(2,1,0)\)が定める平面ABC上に点Pがあり、\(P(2,3,p)\)である。
このとき、\(p\)の値を求めてください。
次は平面のベクトル方程式を用いて、点Pの座標を考えます。
解答をチェックする
平面上にある点のベクトル方程式は、実数\(s,t\)を使って、
\[\vec{OP}=(1-s-t)\vec{OA}+s\vec{OB}+t\vec{OC}\]
と表すことができた。
与えられた条件から、
\begin{eqnarray}
2&=&(1-s-t)4+s(-1)+2t\\
3&=&(1-s-t)1+t\\
p&=&(1-s-t)3+s
\end{eqnarray}
よって、これを整理すると、
\(s=-2,t=6,\)\(p=-11\)
ベクトル方程式 まとめ
今回はベクトル方程について学習しました。
ベクトルを上手く使うことで直線/円/平面を表すことができます。
①ある点aを通る直線

点Aを通り、傾きが\(\vec{d}(\vec{d}\neq0)\)に平行な、直線\(l\)上の点Pは、
\[\vec{OP}=\vec{OA}+t\vec{d} (tは実数)\]
②異なる2点を通る直線

2つの点、A,Bを通る直線l上の点Pは、
\[\vec{OP}=(1-t)\vec{OA}+t\vec{OB} (tは実数)\]
③中心\(a\),半径\(r\)の円

点Aを中心とし、半径rの円上にある点Pのベクトル方程式は、
\begin{eqnarray}
|\vec{AP}|&=&r\\
\Leftrightarrow |\vec{OP}-\vec{OA}|&=&r
\end{eqnarray}
④線分\(AB\)を直径とする円

線分ABを直径とする円上にある点Pのベクトル方程式は、
\begin{eqnarray}
\vec{AP} \cdot \vec{BP}&=&0\\
\vec{OP}-\vec{OA}) \cdot (\vec{OP}-\vec{OB})&=&0
\end{eqnarray}
⑤平面ABC

平面ABC上の点Pのベクトル方程式は、
\[\vec{OP}=(1-s-t)\vec{OA}+s\vec{OB}+t\vec{OC} (s,tは実数)\]
ベクトル方程式には、「ベクトルの内積」についてもしっかりと理解しておく必要があります。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

コメント