[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 30px”]
「ベクトルの面積公式ってなに?」
「三角形の面積をどうやって求めるの?」
[/st-mybox]
今回は数学Bのベクトルから「三角形の面積公式」に関するこんな悩みを解決します。
 高校生
高校生ベクトルを習い始めたばかりで…
ベクトルを用いた三角形の面積は以下の2つがあります。
[st-mybox title=”ベクトルの三角形の面積” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#fafafa” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
①ベクトル表示での公式
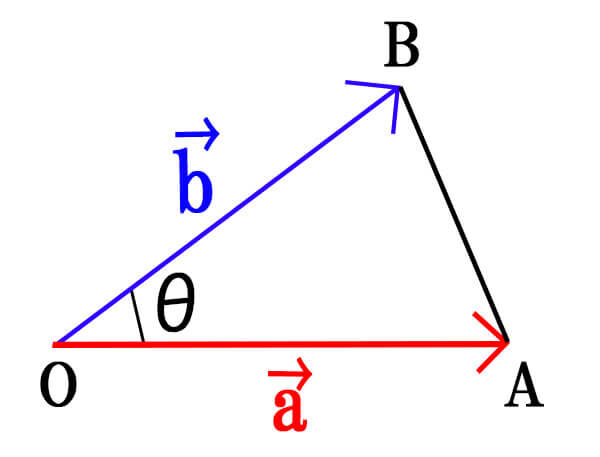
\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}, \vec{OB}=\vec{b}\)とする。このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2} \sqrt{|\vec{a}|^{2}|\vec{b}|^{2}-(\vec{a} \cdot \vec{b})^{2}}\]
②成分表示での公式
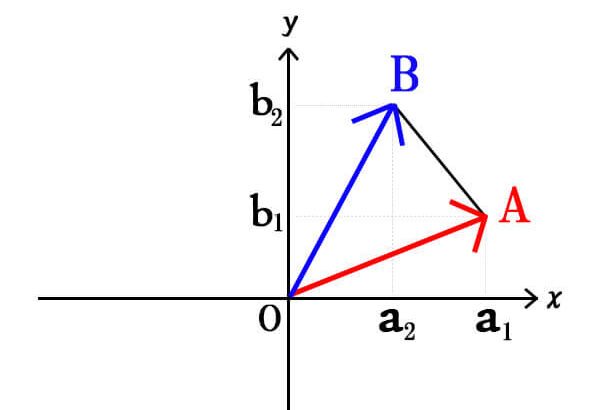
\(\vec{OA}=\vec{a}=(a_{1},a_{2}), \vec{OB}=\vec{b}=(b_{1},b_{2})\)とする。このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2}|a_{1}b_{2}-a_{2}b_{1}|\]
[/st-mybox]
どちらの公式を使うかは問題文で与えられた情報から判断しましょう!
本記事ではベクトルを用いた三角形の面積公式について学習します。
公式を2つ紹介しますので、ぜひ問題に合わせて使いこなせるようになってくださいね!
 シータ
シータベクトルが苦手な方は
ぜひ最後までご覧ください。
それではベクトルを使った三角形の面積の求め方について解説していきましょう。
[st_af id=”13737″]
ベクトルの三角形の面積公式
ベクトルを用いた三角形の面積公式には以下の2つがあります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class shadow” margin=”25px 0 25px 0″]
- ベクトル表示(\(\vec{a,}\vec{b}\)などの表記を使う)の公式
- 成分表示での公式
[/st-mybox]
1つずつゆっくり理解を深めていきましょう。
①ベクトル表示での公式

\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}, \vec{OB}=\vec{b}\)とする。このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2} \sqrt{|\vec{a}|^{2}|\vec{b}|^{2}-(\vec{a} \cdot \vec{b})^{2}}\]
で求めることができる。
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class shadow” margin=”25px 0 15px 0″]
ベクトルの内積\(\vec{a} \cdot \vec{b}\)については別の記事で解説しています。
[st-card myclass=”” id=”14553″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]
[/st-mybox]
②成分表示での公式

ここでは、ベクトルをそれぞれ成分表示で表します。
\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}=(a_{1},a_{2}), \vec{OB}=\vec{b}=(b_{1},b_{2})\)とする。このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2}|a_{1}b_{2}-a_{2}b_{1}|\]
で求めることができる。
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class shadow” margin=”25px 0 15px 0″]
ベクトルの成分表示については別の記事で解説しています。
[st-card myclass=”” id=”14410″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]
[/st-mybox]
ベクトルを使った三角形の面積の求め方
ベクトルを用いた三角形の面積は、先ほど紹介した公式で求められることが分かりました。
ここでは、実際にどう答えを導きだしていくのか、手順を解説します。
[st-mybox title=”例題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
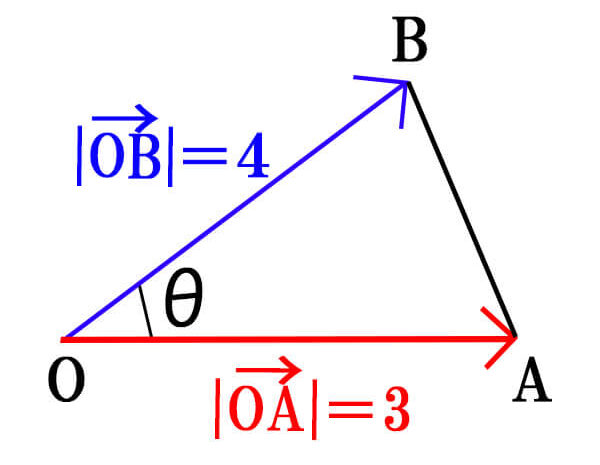
\(|\vec{OA}|=3,|\vec{OB}|=4,\vec{OA} \cdot \vec{OB}=7\)のとき、\(\triangle OAB\)の面積を求めよ。
[/st-mybox]
この問題の場合、ベクトルの大きさと内積が与えられているので、三角形の面積の公式①ベクトル表示での公式が使えることが分かります。
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}\sqrt{|\vec{OA}|^{2}|\vec{OB}|^{2}-(\vec{OA} \cdot \vec{OB})^{2}}\\
\displaystyle &=&\frac{1}{2}\sqrt{3^{2} \cdot 5^{2}-7^{2}}\\
\displaystyle &=&\frac{1}{2} \cdot 4\sqrt{11}\\
&=&2\sqrt{11}
\end{eqnarray}
これで、面積を求めることができました。
[st-mybox title=”例題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
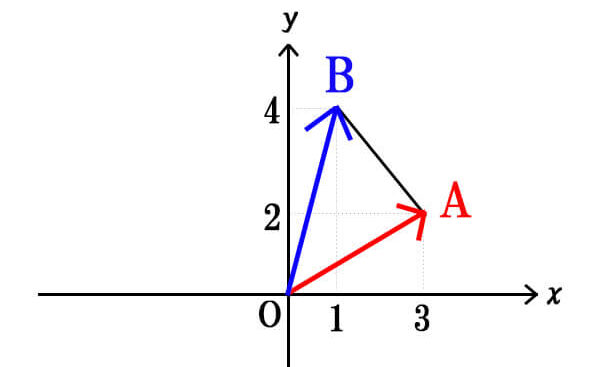
\(O(0,0),A(3,2),B(1,4)\)のとき、\(\triangle OAB\)の面積を求めよ。
[/st-mybox]
この問題の場合、ベクトルの成分表示が与えられているので、三角形の面積の公式②成分表示での公式が使えることが分かります。
\(\vec{OA}=(3,2),\vec{OB}=(1,4)\)であり、
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}|a_{1}b_{2}-a_{2}b_{1}|\\
\displaystyle &=&\frac{1}{2}|3 \cdot 4-2 \cdot 1|\\
\displaystyle &=&\frac{1}{2} \cdot 10\\
&=&5
\end{eqnarray}
三角形の面積公式《証明》
ここからは、先ほどの2つの面積公式の証明をしていきます。
①②それぞれ分けて証明していきます。
①ベクトル表示での公式《証明》

まずは、公式の復習です。
\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}, \vec{OB}=\vec{b}\)とする。このとき\(\triangle OAB\)の面積Sは
\[\displaystyle S=\frac{1}{2}\sqrt{|\vec{a}|^{2} |\vec{b}|^{2}-(\vec{a} \cdot \vec{b})^{2}}\]
を証明していきましょう。
証明:
\(\angle AOB=\theta\)とする。このとき面積Sは、
\[\displaystyle S=\frac{1}{2}|\vec{a}||\vec{b}| \sin\theta\]
\(0<\theta<180^\circ \)より、\(\sin\theta>0\)であるから、
\(\sin^{2}{\theta}+\cos^{2}{\theta}=1\)より
\[\sin \theta=\sqrt{1-\cos^{2}{\theta}}\]
これを先ほどの式に当てはめると、
\[\displaystyle S=\frac{1}{2}|\vec{a}||\vec{b}|\sqrt{1-\cos^{2}{\theta}}\]
ここで、内積の公式 \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos{\theta}\)から
\[\displaystyle \cos{\theta}=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\]
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}|\vec{a}||\vec{b}|\sqrt{1-\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right)^{2}}\\
\displaystyle &=&\frac{1}{2}\sqrt{|\vec{a}|^{2}|\vec{b}|^{2}-{(\vec{a} \cdot \vec{b})}^{2}}
\end{eqnarray}
②成分表示での公式《証明》

まずは、公式の復習です。
\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}=(a_{1},a_{2}), \vec{OB}=\vec{b}=(b_{1},b_{2})\)とする。
このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2}|a_{1}b_{2}-a_{2}b_{1}|\]
では、証明していきましょう。
証明:
\(\vec{OA}=\vec{a}= (a_{1},a_{2}), \vec{OB}=\vec{b}=(b_{1},b_{2})\)であるとき、
ベクトルの大きさと、内積から
\(|\vec{a}|^{2}={a_{1}}^{2}+{a_{2}}^{2}\)
\(|\vec{b}|^{2}={b_{1}}^{2}+{b_{2}}^{2}\)
\(\vec{a} \cdot \vec{b}=a_{1}b_{1}+a_{2}b_{2}\)
であることがわかる。
このとき、
\(\displaystyle S=\frac{1}{2}\sqrt{|\vec{a}|^{2}|\vec{b}|^{2}-(\vec{a} \cdot \vec{b})^{2}}\) (①ベクトル表示での公式より)
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}\sqrt{({a_{1}}^{2}+{a_{2}}^{2})({b_{1}}^{2}+{b_{2}}^{2})-(a_{1}b_{1}+a_{2}b_{2})^{2}}\\
\displaystyle &=&\frac{1}{2}\sqrt{{a_{1}}^{2}{b_{2}}^{2}-2a_{1}b_{1}a_{2}b_{2}+{a_{2}}^{2}{b_{1}}^{2}}\\
\displaystyle &=&\frac{1}{2}\sqrt{{(a_{1}b_{2}-a_{2}b_{1})}^{2}}\\
\displaystyle &=&\frac{1}{2}|(a_{1}b_{2}-a_{2}b_{1})|
\end{eqnarray}
ベクトルの三角形の面積《練習問題》
ここからはベクトルを用いた三角形の面積問題を2問紹介します。
[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{OA}=3,\ \vec{OB}=4,\ \angle AOB=30^\circ\)である。\(\triangle OAB\)の面積Sを求めよ。
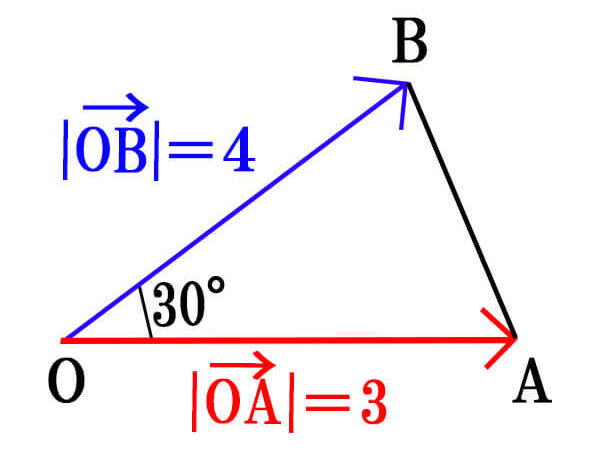
[/st-mybox]
解答をチェックする
まず、\(\vec{OA} \cdot \vec{OB}\)を求める。
\begin{eqnarray}
\vec{OA} \cdot \vec{OB}&=&|\vec{OA}||\vec{OB}|\cos 30^\circ\\
&=&3 \times 4 \times \frac{\sqrt{3}}{2}\\
&=&6\sqrt3
\end{eqnarray}
ここで
\[\displaystyle S=\frac{1}{2}\sqrt{|\vec{OA}|^{2}|\vec{OB}|^{2}-(\vec{OA} \cdot \vec{OB})^{2}}\]
より、
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}\sqrt{3^{2} \cdot 4^{2}-(6 \sqrt{3})^{2}}\\
\displaystyle &=&\frac{1}{2}\sqrt{9 \cdot 16-108}\\
&=&3
\end{eqnarray}
[st-mybox title=”練習問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
座標平面上に、\(A(2,4),B(4,1),C(-1,0)\)がある。このとき\(\triangle ABC\)の面積Sを求めよ
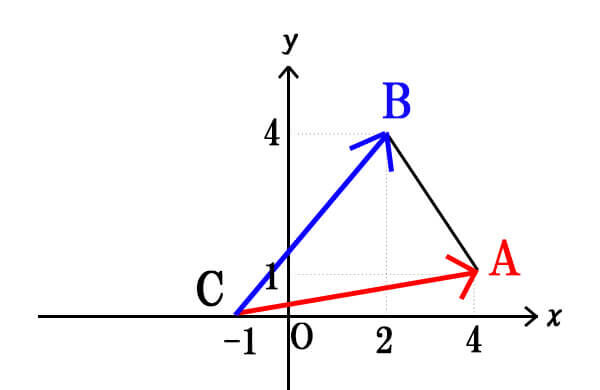
[/st-mybox]
[st-slidebox fontawesome=”fa-check” text=”解答をチェックする” bgcolor=”#f1f1f1″ color=”#1a1a1a” margin_bottom=”20″]
②の公式を使うために、どこか1点を平行移動させて原点に持ってきます。
3点を同じ方向に、同じ距離平行移動しても三角形の面積の大きさは変わらないため、この方法で解いていきます。
今回は、点C(-1,0)を原点に平行移動させます。(x方向に+1平行移動)
他の点も、同じようにx方向に+1平行移動させると、点A(2,4)→点A'(3,4)、点B(4,1)→点B'(5,1)となります。
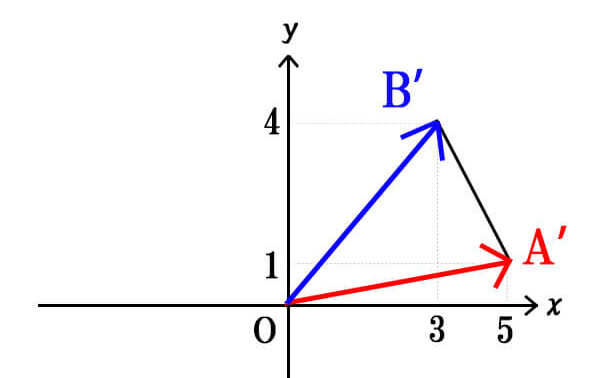
求めたい三角形の面積Sは、\(\triangle OA^{\prime}B^{\prime}\)の面積と同じであるから、
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}|3 \cdot1-5 \cdot4|\\
\displaystyle &=&\frac{1}{2} \cdot 17\\
\displaystyle &=&\frac{17}{2}
\end{eqnarray}
[/st-slidebox]
 高校生
高校生三角形の面積の求め方がだいぶ分かってきました!
 シータ
シータ素晴らしいね!覚えているうちに、たくさん練習しよう!
ベクトルの三角形の面積 まとめ
今回はベクトルを用いた三角形の面積について学習しました。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
ベクトルを用いた三角形の面積公式には以下の2つがありました。
- ベクトル表示(\(\vec{a,}\vec{b}\)などの表記を使う)の公式
- 成分表示での公式
[/st-mybox]
[st-minihukidashi fontawesome=”” fontsize=”” fontweight=”” bgcolor=”#FFB74D” color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]ベクトルのなす角[/st-minihukidashi]
[st-mybox title=”ベクトルのなす角” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
①ベクトル表示での公式

\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}, \vec{OB}=\vec{b}\)とする。このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2} \sqrt{|\vec{a}|^{2}|\vec{b}|^{2}-(\vec{a} \cdot \vec{b})^{2}}\]
で求めることができる。
②成分表示での公式

ここでは、ベクトルをそれぞれ成分表示で表します。
\(\triangle OAB\)があり、\(\vec{OA}=\vec{a}=(a_{1},a_{2}), \vec{OB}=\vec{b}=(b_{1},b_{2})\)とする。このとき\(\triangle OAB\)の面積Sは、
\[\displaystyle S=\frac{1}{2}|a_{1}b_{2}-a_{2}b_{1}|\]
で求めることができる。
[/st-mybox]
ベクトルで面積を求めるには、「ベクトルの内積」についてもしっかりと理解しておく必要があります。
ベクトルの内積はこちらの記事で詳しく解説しています。
[st-card myclass=”” id=”14675″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

