「隣り合うってどういうこと?」
「隣り合わない順列の解き方が分からない」
順列の問題を解いていると、「隣り合う順列」と「隣り合わない順列」という言葉が出ててきますよね。
この2つは解き方が大きく違うので、しっかり理解しておく必要があります。
そこで今回はこのような問題を解けるようにしていきます。
男子3人と女子4人を以下のように並べるとき、その並べ方は何通りありますか。
- (1) 男子3人が隣り合う
- (2) 男子が隣り合わない
- (3) 少なくとも2人の男子が隣り合う
- (4) 男子3人のうち2人だけが隣り合う
本記事では、隣り合う順列と隣り合わない順列の解き方を解説します。
隣り合うときのポイント

隣り合うときのポイントは、隣り合う1つの集団をひとかたまりと見なして並べることです
隣り合うときの順列は、まずは隣り合うものを1つの塊とみなして並び替えます。
そのあとに、塊の中で並び替えをします。
隣り合わないときのポイント
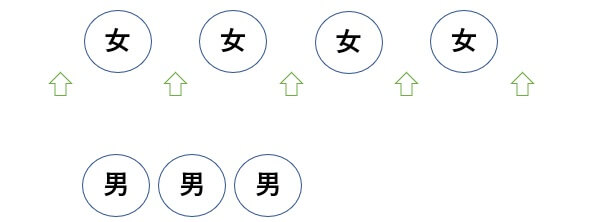
隣り合わないときのポイントは、隣り合わせたくないもの以外を並べたあとに、両端もしくは間に隣り合わせたくないものを入れていくことです。
隣り合わないというのは、交互に並べていくイメージです。
今日の課題
では、解き方のポイントを使って今日の課題を解いていきましょう。
男子3人と女子4人を以下のように並べるとき、その並べ方は何通りありますか。
- (1) 男子3人が隣り合う
- (2) 男子が隣り合わない
- (3) 少なくとも2人の男子が隣り合う
- (4) 男子3人のうち2人だけが隣り合う
(1) 男子3人が隣り合う
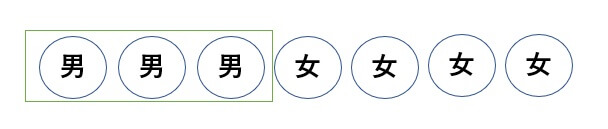
これは隣り合うときの問題なので、男子3人を1つの塊とみなしましょう。
そうすることで、問題が男子の塊と女子4人の並び替えに変わります。
男子の塊と女子4人の並び方の総数は、
\(5!=5・4・3・2・1=120\)通り
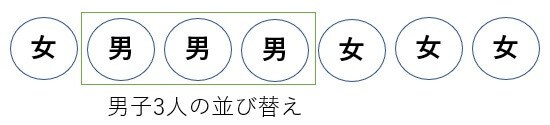
次に、男子の塊の中でも並び替えがあるので
\(3!=3・2・1=6\)通り
したがって、男子3人が隣り合う並び方は
\(120\times{6}=720\)
答え 720通り
(2) 男子が隣り合わない
今回は隣り合わない問題なので、女子を並び替えて、あとから両端と間に男子を入れていきます。

まず女子を並び替えます。
\(4!=4・3・2・1=24\)通り
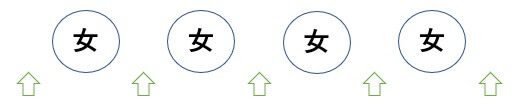
つぎの男子3人を入れる箇所を選びます。
\[_{5}C_{3}=\displaystyle \frac{5\times{4}\times{3}}{3\times{2}\times{1}=10}\]
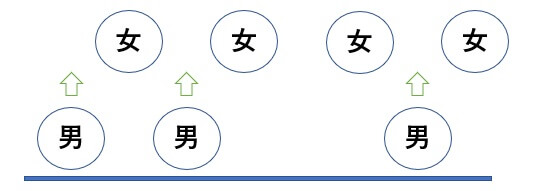
入れる男子の順番を決めます。
\(3!=3・2・1=6\)通り
よって男子が隣り合わない時の並び方の総数は
\(24\times{10}\times{6}=1440\)
答え 1440通り
(3) 少なくとも2人の男子が隣り合う
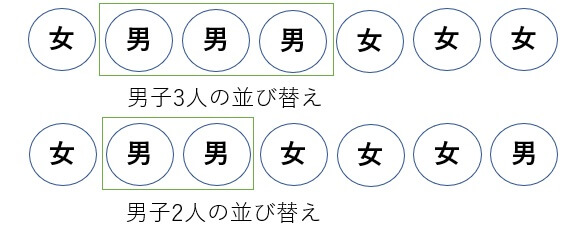
「少なくとも2人の男子が隣り合う」の補集合は「男子が隣り合わない」
よって、男子3人と女子4人の並び替えの総数から、「男子が隣り合わない」並び方を引けば「少なくとも2人の男子が隣り合う」並び方が求められる。
男子3人と女子4人の並び替えの総数は
\(7!=7・6・5・4・3・2・1=5040\)通り
(2)で男子が隣り合わない並び方の総数は1440通りと求められているので、
\(5040-1440=3600\)
答え 3600通り
(4) 男子3人のうち2人だけが隣り合う

まず女子を並べて、その両端または間に男子2人組と1人を入れていく。
女子の並び方が
\(4!=4・3・2・1=24\)通り
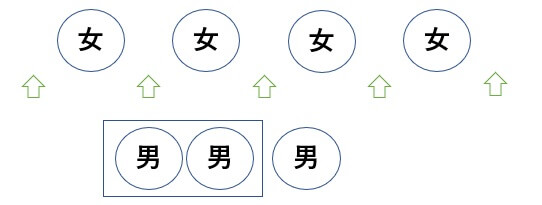
男子3人から2人を並べる
\(_{3}P_{2}=3・2=6\)通り
そして2人組を入れる場所が5か所
男子1人を入れる場所が4か所
したがって、
\(24\times{6}\times{5}\times{4}=2880\)
答え 2880通り
練習問題

問題1 男子2人と女子3人が1列に並ぶとき,男子2人が隣り合う並び方は何通りあるか。
解説
男子2人をセットにして、その並び方は2通りである。
また、男子ペアと女子3人で並ぶときの並び方は
\(4!=4・3・2・1=24\)通り
よって、男子2人が隣り合う並び方は
\(2\times{24}=48\)
答え 48通り
問題2 男子4人と女子3人が1列に並ぶとき,女子A,B,CのうちAとBが隣り合い、BとCが隣り合わない並び方は何通りあるか。
解説
まず男子4人を並べる。
\(4!=4・3・2・1=24\)通り
男子の両端とその間の5か所のうち1か所にAとBを並べていれる。
そのときAB,BAの2つの並び方があるので
\(5\times{2}=10\)通り
最後にBの隣を除く5か所のうちの1か所にCをいれる。
したがって、
\(24\times{10}\times{5}=1200\)
答え 1200通り
隣り合う順列 まとめ
今回は数学Aの順列から、「隣り合う順列」と「隣り合わない順列」とまとめました。
隣り合う順列は、隣り合うものを1つの塊(セット)として考える。
隣り合わない順列は、隣り合わせたくないもの以外で並べたあとに、両端もしくは間に隣り合わせたくないものを入れていく。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!

