数学Ⅰ三角比のなかで多くの高校生を困らせるのが「余弦定理」ですね。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 40px”]
「余弦定理の公式が知りたい」
「余弦定理の使い方が分からない」
[/st-mybox]
今回は三角比の中から”余弦定理”に関するこんな悩みを解決します。
 高校生
高校生余弦定理が良く分からなくて…
さっそくですが、辺BCの長さがいくつになるか分かりますか?
[st-mybox title=”余弦定理の例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(AB=4,AC=3\sqrt{3},\angle A=30^\circ \)のとき、辺BCの値を求めよ。
[/st-mybox]
「これだけの情報では求められないですよ」
そう思った方は余弦定理が使えていないので危険です。
実は「余弦定理」を使えば辺BCの長さを簡単に求めることができます!
[st-mybox title=”余弦定理の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
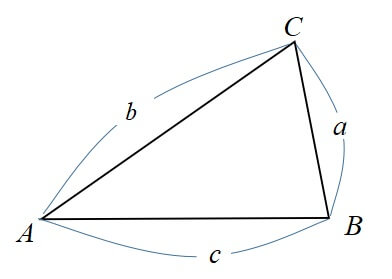
\(△ABC\)において各辺を\(a,b,c\)とするとき、以下の公式が成り立つ。
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc \cos A\\
b^{2}&=&a^{2}+c^{2}-2ac \cos B\\
c^{2}&=&a^{2}+b^{2}-2ab \cos C\\
\end{eqnarray}
[/st-mybox]
本記事では余弦定理の公式の使い方や証明について解説していきます。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
余弦定理の公式
余弦定理は三角形の辺や角の大きさを求められる定理です。
[st-mybox title=”余弦定理の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(△ABC\)において各辺を\(a,b,c\)とするとき、以下の公式が成り立つ。
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc \cos A\\
b^{2}&=&a^{2}+c^{2}-2ac \cos B\\
c^{2}&=&a^{2}+b^{2}-2ab \cos C\\
\end{eqnarray}
[/st-mybox]
余弦定理は辺の長さと三角比を用いた重要定理の1つです。
⇓余弦定理の公式を変形することで角の大きさを求めることもできます。
\begin{eqnarray}
\displaystyle \cos A&=&\frac{b^{2}+c^{2}-a^{2}}{2bc}\\
\displaystyle \cos B&=&\frac{a^{2}+c^{2}-b^{2}}{2ac}\\
\displaystyle \cos C&=&\frac{a^{2}+b^{2}-c^{2}}{2ab}
\end{eqnarray}
余弦定理の使い方
冒頭で登場した余弦定理の例題を一緒に解いてみましょう。
[st-mybox title=”余弦定理の例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(AB=4,AC=3\sqrt{3},\angle A=30^\circ \)のとき、辺BCの値を求めよ。

[/st-mybox]
2辺とその間の角の大きさが分かっているので、向かい合う辺BCの大きさを求めることができます。
辺ABの大きさを\(a\)とすると正弦定理より、
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc \cos A\\
a^{2}&=&(3\sqrt{3})^{2}+4^{2}-2 \times (3\sqrt{3}) \times 4 \times \cos 30^\circ\\
a^{2}&=&27+16-36\\
a^{2}&=&7
\end{eqnarray}
\(a>0\)なので
\[a=\sqrt{7}\]
したがって、BCの大きさは\(\sqrt{7}\)である。
このように余弦定理は辺の長さを求めるときに使います。
 高校生
高校生辺や角の大きさを代入するだけですね!
余弦定理の公式 証明
余弦定理の使い方を確認したところで、なぜ余弦定理が成り立つのか証明してみましょう。
\([1] 0^\circ < A < 90^\circ\)のとき
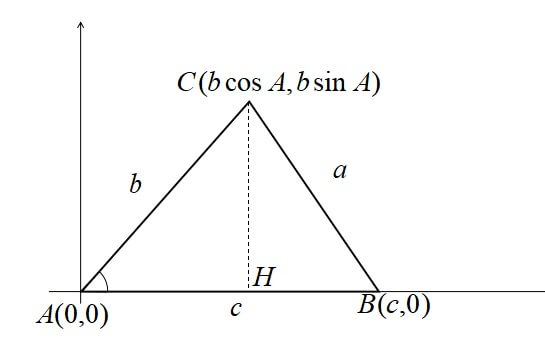
上の図のように点A,B,Cをとる。
\(A(0 , 0)、B(c , 0)\)とすると、Cは\((b \cos A , b \sin A)\)となる。
頂点CからX軸へ垂線を下して、その交点をHとおく。
三角形\(CHB\)に注目して三平方の定理を用いると、
\begin{eqnarray}
a^{2} &=& |c – b \cos A|^{2} + (b \sin A)^{2}\\
&=& c^{2} – 2bc・\cos A + b^{2} (\cos^{2}A + \sin^{2}A)
\end{eqnarray}
すなわち
\(a^{2} = b^{2} + c^{2} – 2bc・\cos A\) となる。
\([2] A = 90^\circ\)のとき
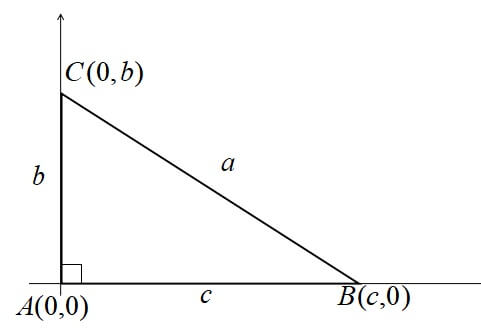
角Aが直角の場合、△ABCは直角三角形になる。
三平方の定理より
\(a^{2}=b^{2}+c^{2}\)
となる。
\(\cos A = \cos 90 = 0\)であることから、
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc \cos A\\
a^{2}&=&b^{2}+c^{2}
\end{eqnarray}
よって、角Aが直角の場合も
\(a^{2} = b^{2} + c^{2} – 2bc・\cos A\) が成立する。
\([3] 90^\circ < A < 180^\circ\)のとき
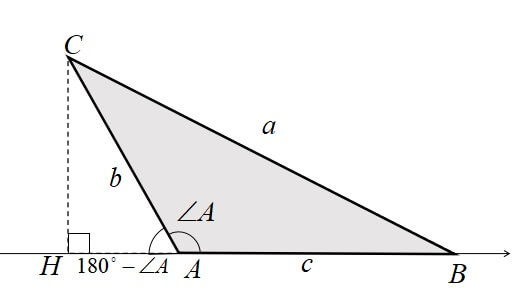
上の図より、BHとCHは以下のようになる。
\begin{eqnarray}
BH&=&c+AH\\
&=&c+b \cos (180^circ-A)\\
&=&c-b \cos A
\end{eqnarray}
\begin{eqnarray}
CH&=&b \sin (180^circ-A)\\
&=&b \sin A
\end{eqnarray}
\(BCH\)に置いて、三平方の定理より
\(BC^{2}=BH^{2}+CH^{2}\)
したがって
\begin{eqnarray}
a^{2}&=&(c-b \cos A)^{2} + b^{2} \sin^{2}A\\
&=&(c^{2}-2bc \cos A+b^{2} \cos^{2}A)+b^{2} \sin^{2}A\\
&=&c^{2}-2bc・cosA+b^{2}
\end{eqnarray}
したがって、
\(a^{2}=b^{2}+c^{2}-2bc・cosA\) は成立する
\([1][2][3]\)より余弦定理の証明終了。
余弦定理の公式<練習問題>

今回学んだ「余弦定理」を用いて、練習問題に挑戦してみましょう。
今回は2つのパターンの練習問題を用意しました。
- 辺の長さを求める問題
- 角の大きさを求める問題
[st-mybox title=”余弦定理の例題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
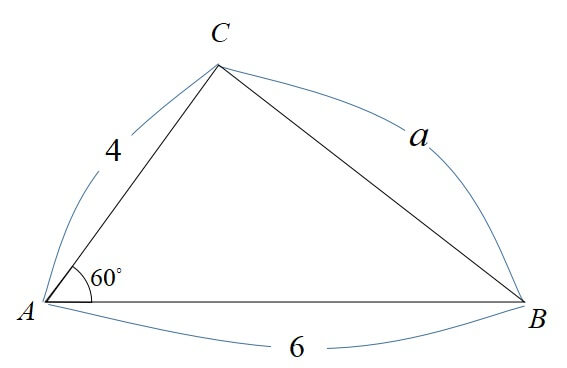
\(AC=4,AB=6,\angle A=60^\circ\)の三角形ABCにおいて、辺BCの長さを求めよ。
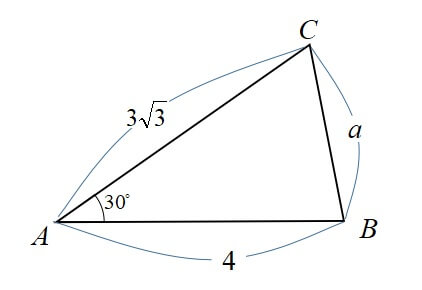
[/st-mybox]
解説
余弦定理より、
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc \cos A\\
a^{2}&=&4^{2}+6^{2}-2 \times 4 \times 6 \times \cos 60^\circ \\
a^{2}&=&16+36-24\\
a^{2}&=&28
\end{eqnarray}
\(a>0\)なので
\(a=2\sqrt{7}\)
したがって、
辺BCの長さは、\(2\sqrt{7}\)である。
次は余弦定理を用いて角度の大きさを求める練習問題を解いてみましょう。
[st-mybox title=”余弦定理の例題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(AC=6,AB=2\sqrt{2},BC=2\sqrt{5}\)の三角形ABCにおいて、角\(A\)の角の大きさを求めよ。
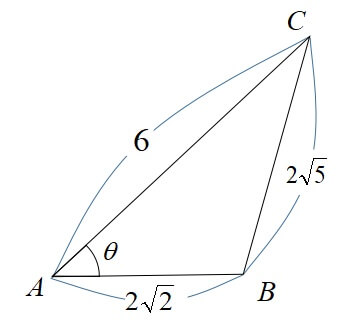
[/st-mybox]
余弦定理
\(a^{2}=b^{2}+c^{2}-2bc \cos A\)を変形して
\[\displaystyle \cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc} \]
変形した式に分かっている値を代入していく
\begin{eqnarray}
\displaystyle \cos A&=&\frac{b^{2}+c^{2}-a^{2}}{2bc} \\
\displaystyle &=&\frac{6^{2}+(2\sqrt{2})^{2}-(2\sqrt{5})^{2}}{2\times 6 \times 2\sqrt{2}} \\
\displaystyle &=&\frac{36+8-20}{24\sqrt{2}} \\
\displaystyle &=&\frac{24}{24\sqrt{2}} \\
\displaystyle &=&\frac{1}{\sqrt{2}}
\end{eqnarray}
\(0 < \angle A < 180^\circ\)
なので
\(A=45^\circ\)
余弦定理の公式 まとめ
今回は数学Ⅰの三角比から「余弦定理の公式」についてまとめました。
[st-minihukidashi fontawesome=”” fontsize=”” fontweight=”” bgcolor=”#FFB74D” color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]余弦定理 まとめ[/st-minihukidashi]
[st-mybox title=”余弦定理の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(△ABC\)において各辺を\(a,b,c\)とするとき、以下の公式が成り立つ。
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc \cos A\\
b^{2}&=&a^{2}+c^{2}-2ac \cos B\\
c^{2}&=&a^{2}+b^{2}-2ab \cos C\\
\end{eqnarray}
[/st-mybox]
余弦定理を使うことで、辺の長さや角の大きさを求めることができます。
[st-mybox title=”正弦定理と余弦定理” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
正弦定理を使う時
①1辺と2つの角が与えられている場合
②1組の向かい合う辺と角が与えられている場合
③外接円の半径を求めたい場合
余弦定理を使う時
①2辺とその間の角が与えられている場合
②3辺が与えられているとき
[/st-mybox]
そして、余弦定理とあわせて理解したいのが正弦定理です。
[st-card myclass=”” id=”2296″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
三角関数には重要な公式がたくさんあります。
三角関数の重要ポイントをまとめた記事はこちら
[st-card myclass=”” id=”2005″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

