導出したい三角関数を選択してください。
角度を入力してください。
になります。
三角関数に苦手意識がある高校生は必見!
\(\sin,\cos,\tan\)の値を暗記するのは効率が悪すぎます!

三角比の値を暗記していると
「\(\displaystyle \sin 60°\)っていくつだっけ…忘れしてしまった…」
テストでこんなことになるので危険です!
下の表は三角比の一覧表ですが、これを丸暗記しても応用力が身に付きません。
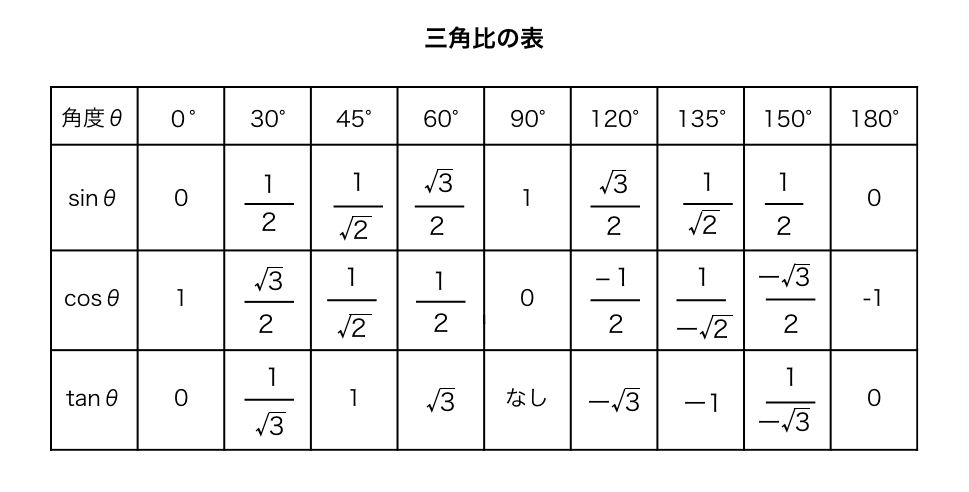
三角比は各値を暗記するのではなく、各値の求め方を知っておくことが大切です。
本記事は三角比の求め方と覚え方を解説します。
その他の三角関数の公式については「三角関数が分かる!重要公式の使い方を丁寧に解説!」にまとめました。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
三角比の公式
まず原点\(O\)を中心とする半径\(r\)の円を描きます。
\(x\)軸の正の方向に対して、線分\(OA\)による角の大きさを\(\angle AOB=\theta \)とするとき、
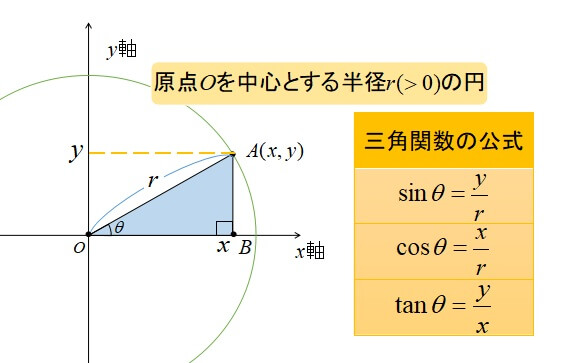
この直角三角形において各辺の比を表したものが三角比です。
[st-mybox title=”三角比の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”bluekoushiki st-mybox-class” margin=””]
\begin{eqnarray}
\sin \theta &=& \displaystyle \frac{y}{r}\\
\cos \theta &=& \displaystyle \frac{x}{r}\\
\tan \theta &=& \displaystyle \frac{y}{x}
\end{eqnarray}
[/st-mybox]
まだピンと来ていない人のために、実際に数字を入れてみましょう!
三角関数では中心角を\(360^\circ\)ではなく、\(2\pi\)と表します。
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
この表し方は弧度法といい、「弧度法とは?弧度法の変換や面積公式すべて解説!」で解説しています。
[/st-mybox]
以下の3つは三角比の代表的な三角形です。
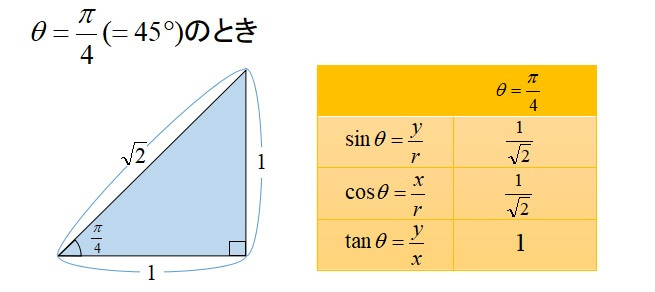

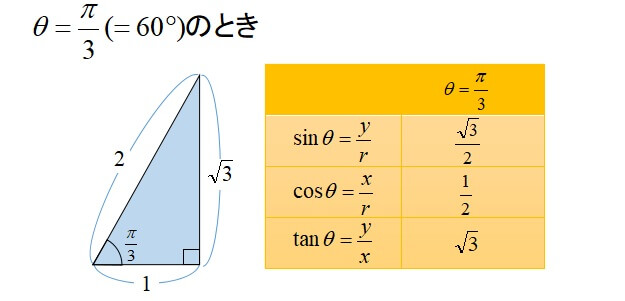
このように、斜辺の長さ、\(x\)座標、\(y\)座標が分かっていれば三角比を表すことができます。
また、\(90^\circ\)を超える場合も、三角形をイメージすることで三角比を求めることができます。
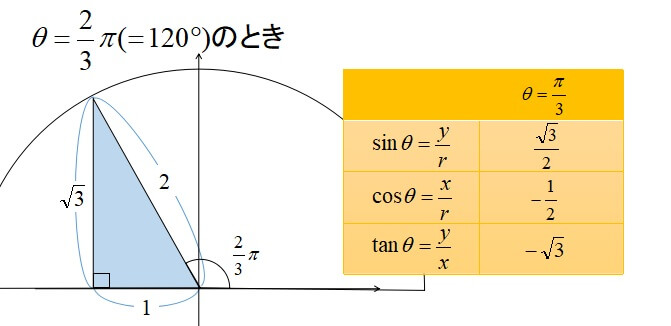
三角比(sin,cos,tan)の覚え方

 高校生
高校生sin60°の値などが覚えられないです…
三角比の表は暗記してはいけません。
それは効率が悪すぎるうえにテストで絶対に忘れます。
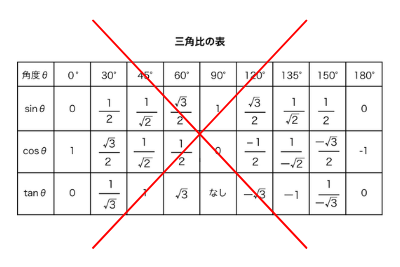
なので、表を覚えるのではなくて求め方を覚えてください。
sin,cos,tanのアルファベットの頭文字に注目します。
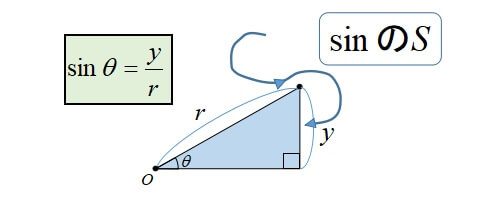
\(\sin\)を求めるときは、Sを描くように数字を代入しましょう。

\(\cos\)は分かりやすいですね。\(\theta\)を挟むように各辺の値を代入しましょう。
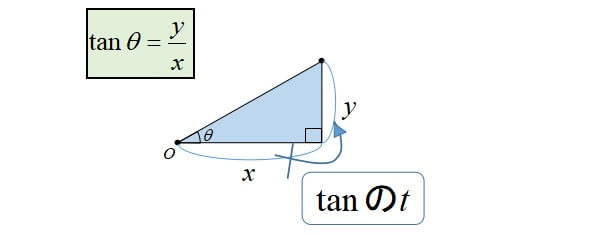
\(\tan\)は無理やり感がありますが、この順で代入することで求めることができます。
テストで忘れるので三角比の表を暗記するのではなく求め方を覚えましょう。
 高校生
高校生この動きを覚えておけばできそうです!
三角比が表すもの
「そもそも三角比ってなに!」
そんな声が聞こえてきそうですね。
“三角比”とは「三角形の各辺の比」を表しています。
そう言っても難しいので図で解説していきましょう。
下の図のような三角形があったとします。
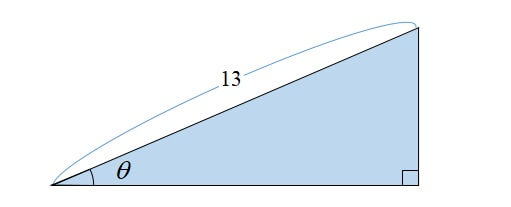
この三角形の三角関数が\(\sin \theta=\displaystyle \frac{5}{13}\)、\(\cos \theta=\displaystyle \frac{12}{13}\)と分かっているならば
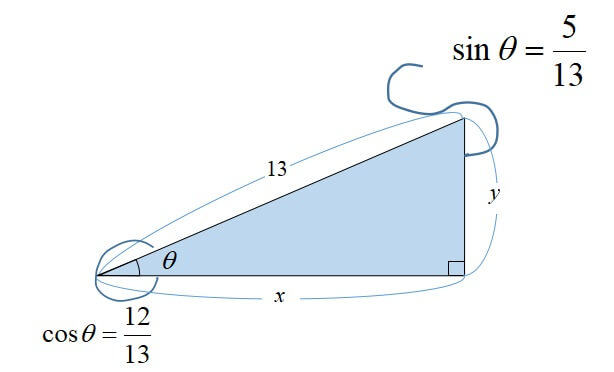
斜辺の長さ13にsinを掛ける\(y\)の長さが分かります。
\begin{eqnarray}
y&=&13\times \sin \theta\\
\displaystyle &=&13 \times \frac{5}{13}\\
&=&5
\end{eqnarray}
また、斜辺の長さ13にcosを掛けると\(x\)の長さが分かります。
\begin{eqnarray}
x&=&13\times \cos \theta\\
\displaystyle &=&13 \times \frac{12}{13}\\
&=&12
\end{eqnarray}
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#fafafa” borderwidth=”2″ borderradius=”4″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
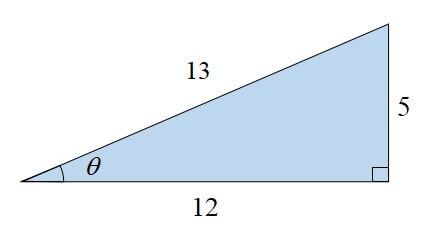
斜辺の長さ13にsinを掛けると縦の辺の長さが分かります。
斜辺×\(\sin\)=縦の辺
また、斜辺の辺の長さ13にcosを掛けると横の長さが分かります。
斜辺×\(\cos\)=横の辺
[/st-mybox]
三角比を用いることで、各辺の長さを求めることができます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#FFFDE7″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”19px”]
斜辺の長さ × \(\sin\) ⇒縦の辺の長さ
斜辺の長さ × \(\cos\) ⇒横の辺の長さ
横の辺の長さ × \(\tan\) ⇒縦の長さ
[/st-mybox]
三角比のまとめ記事もぜひご覧ください。
⇒三角関数が分かる!重要公式の使い方を丁寧に解説!
三角比の公式<練習問題>

三角比の公式を使って練習問題を解いてみましょう。
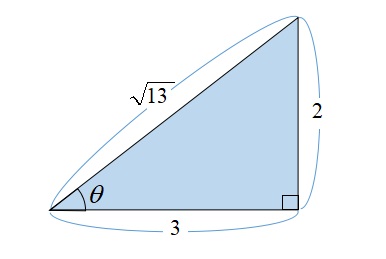
下の三角形の\(\sin \theta\)、\(\cos \theta\)、\(\tan \theta\)を求めよ。
解答
\(\sin \theta\)は斜辺に対してアルファベットのSの動きで求めることができました。

したがって、斜辺の長さが\(\sqrt{13}\)で、縦の長さが\(2\)なので、
\[\sin \theta=\displaystyle \frac{2}{\sqrt{13}}=\frac{2\sqrt{13}}{13}\]
最後は分母からルートが無くなるように有理化をしました。
これで\(\sin \theta\)の値を求めることができました。
次に\(\cos \theta\)を求めます。
\(\cos \theta\)は斜辺に対してアルファベットのCの動きで求めることができます。

斜辺の長さが\(\sqrt{13}\)で、縦の長さが\(3\)なので、

\[\cos \theta=\displaystyle \frac{3}{\sqrt{13}}=\frac{3\sqrt{13}}{13}\]
\(\cos \theta\)の値を求めることができました。
最後に\(\tan \theta\)の値を求めます。
\(\tan \theta\)は縦の長さを横の長さで割ると求められます。


横の長さが3で、縦の長さが2なので、
\[\tan \theta=\displaystyle \frac{2}{3}\]
これで\(\sin \theta , \cos \theta , \tan \theta\)の値を求めることができました。
このようにアルファベットs,c,tの動きを覚えていれば、\(\sin , \cos , \tan \)の値を求めることができます。
[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
下の三角形において、\(\sin \theta=\displaystyle \frac{3}{5}\)、\(\cos \theta=\displaystyle \frac{4}{5}\)のとき、\(x,y\)の値を求めよう。
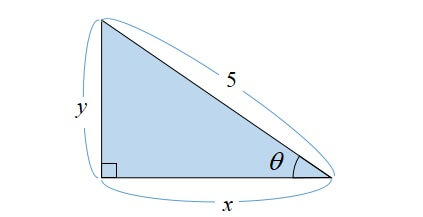
[/st-mybox]
解答
三角比が分かっている状態で、各辺の長さを求める練習をします。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#FFFDE7″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]
- 斜辺の長さ × sin ⇒縦の辺の長さ
- 斜辺の長さ × cos ⇒横の辺の長さ
- 横の辺の長さ × tan ⇒縦の長さ
[/st-mybox]
縦の長さ\(y\)は、斜辺に長さに\(\sin \theta \)を掛けることで求められます。
\begin{eqnarray}
y&=&5\times \sin \theta\\
\displaystyle &=&5 \times \frac{3}{5}\\
&=&3
\end{eqnarray}
横の長さは\(x\)は、斜辺の長さに\(\cos \theta \)を掛けると求められます。
\begin{eqnarray}
x&=&5 \times \cos \theta\\
\displaystyle &=&5 \times \frac{4}{5}\\
&=&4
\end{eqnarray}
以上が練習問題でした。
各辺の長さや三角比を求められるようにしましょう。
 高校生
高校生表を暗記するよりも簡単でした!
三角比のおすすめ勉強法

1年生で三角比を学習し、2年生で三角関数を勉強します。
三角関数は受験でも頻出単元なので、いま三角比を得意にしておくと来年の三角比が少し楽になります。
[st-mybox title=”三角比の勉強方法” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 教科書やノートを振り返る
- 問題種で応用力を磨く
- 分かりやすい授業を受ける
[/st-mybox]
自分の理解度と目標に合わせて、自分に合った勉強法を試してみてください。
 シータ
シータ3つの勉強法を紹介するよ
教科書やノートを見直す

まずは基本に立ち返って、教科書・ノートを見直してみましょう。
特に基礎が不安な方はまず教科書の復習をしてみて下さい。
三角比の意味や覚え方もまとまっているはずです。
 シータ
シータ基本問題が不安なら教科書がおすすめ!
問題集で応用力を磨く

用語や公式を覚えたら問題集で応用力を磨きましょう。
- 教科書の例題
- 問題集の基本問題
- 問題集の応用問題
問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。
分かりやすい解説を見る
以下のような悩みがあるなら、映像授業もおすすめです。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 勉強しても成績が伸びない
- 学校の授業が分かりにくい
- 分からない所が分からない
[/st-mybox]
映像授業なら自分に必要な授業だけを、分かるまで視聴することができます。
分からないを残すことなく、定期テスト対策ができるので授業授業がおすすめです。
三角比の公式(sin,cos,tan) まとめ
今回は三角比の公式と覚え方をまとめました。
これは基礎中の基礎なので、しっかりと押さえておきましょう。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]三角比の公式 まとめ[/st-marumozi]

[st-mybox title=”三角比の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”bluekoushiki st-mybox-class” margin=””]
\begin{eqnarray}
\sin \theta &=& \displaystyle \frac{y}{r}\\
\cos \theta &=& \displaystyle \frac{x}{r}\\
\tan \theta &=& \displaystyle \frac{y}{x}
\end{eqnarray}
[/st-mybox]
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#FFFDE7″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”19px”]
斜辺の長さ × sin ⇒縦の辺の長さ
斜辺の長さ × cos ⇒横の辺の長さ
横の辺の長さ × tan ⇒縦の長さ
[/st-mybox]
三角比の表を丸暗記するのではなく、三角形の辺の長さから三角比を求められるようになりましょう。
三角比には重要な公式がたくさんあります。
正弦定理や余弦定理についても別記事でまとめています。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]

