[st-mybox title=”” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
「対数logのグラフの形が分からない」
「対数関数のグラフが書き方は?」
[/st-mybox]
対数関数のグラフがイメージできない方は必見!
今回は対数関数のグラフに関する悩みを解決します。

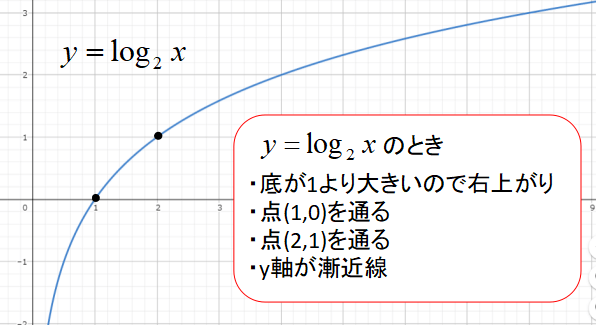
対数関数\(y=log_{a}x\)をグラフにすると以下のような形になります。
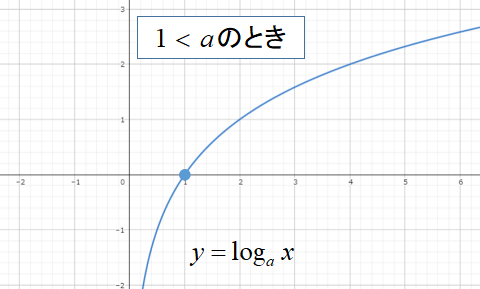
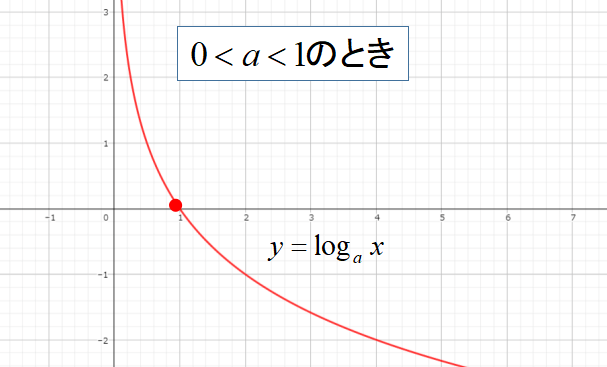
対数関数のグラフはなかなか書くことがないので、グラフの形を忘れてしまいますよね。
本記事では対数関数のグラフの特徴と書き方を解説しました。
この記事を読んで対数関数のグラフの特徴と書き方をぜひ覚えていってください。
[st_af id=”13740″]
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
対数関数のグラフ
\(y=log_{a}x\)のような関数を、\(a\)を底とする\(x\)の対数関数といいます。
[st-mybox title=”対数関数” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1,x>0\)とするとき、以下のような関数を対数関数という。
\[y=log_{a}x\]
[/st-mybox]
\(log_{a}x\)の\(a\)の部分を底(てい)、\(x\)の値を真数(しんすう)といいます。

 シータ
シータ対数と指数の関係をしっかり押さえておこう
対数関数のグラフの形
対数関数をグラフで表すときは、底の値に注意しましょう。
\(a>1\)のときは、右上がりのグラフになります。
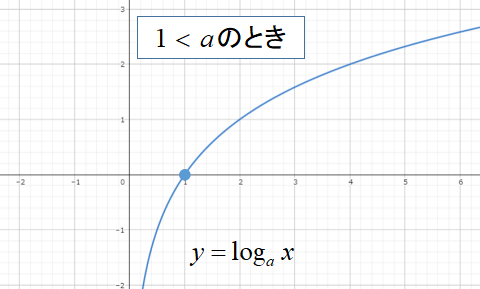
\(0<a<1\)のときは、右下がりのグラフになります。
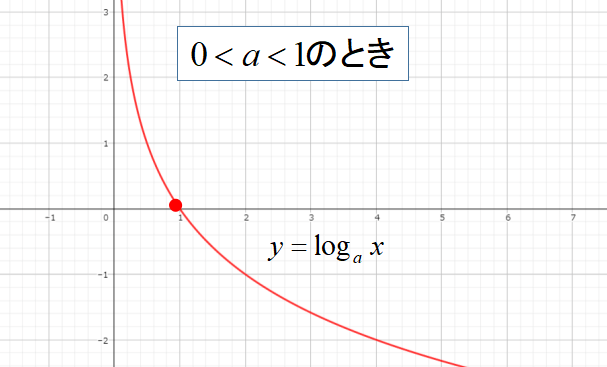
 高校生
高校生滑らかな曲線になるんですね!
対数関数のグラフの特徴
対数関数のグラフの特徴をまとめました。
[st-mybox title=”対数関数のグラフの特徴” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(1,0)を通る
- a>1のとき右上がりで、点(a,1)を通る
- 0<a<1のとき右下がりで、点(\(\displaystyle \frac{1}{a}\),-1)を通る
- y軸が漸近線
[/st-mybox]
\(y=log_{2}x\)のグラフだと点(1,0)(2,1)を通ります。
指数関数と対数関数
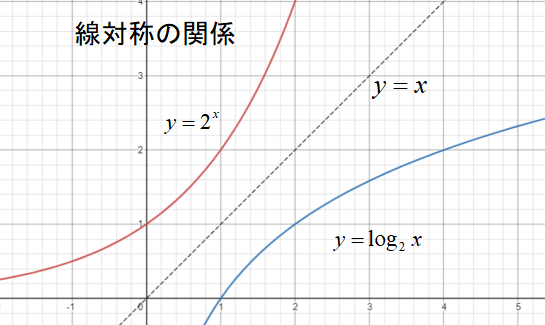
対数関数と密接な関係をもつのが指数関数です。
一般に、対数関数\(y=log_{a}x\)のグラフは、指数関数\(y=a^{x}\)のグラフと直線\(y=x\)に関して線対称のグラフになります。
対数と指数には以下のような関係があります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[y=log_{a}x \Leftrightarrow a^{y}=x\]
[/st-mybox]
指数表記と対数表記をスムーズに入れ替えれるようにしましょう。
[st-mybox title=”関連” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
対数logについて詳しく知りたい方はこちらを先にご覧ください。
[/st-mybox]
 シータ
シータ対数はaを何乗したらxになるのかを表しているよ
対数関数のグラフの書き方
対数関数のグラフは以下の3ステップで書くことができます。
[st-mybox title=”対数関数のグラフの書き方” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(1,0)に目印をつける
- a>1ならば点(a,1)に目印を付ける。
0<a<1ならば点(\(\displaystyle \frac{1}{a},-1\))に目印を付ける。 - y軸を漸近線にして、滑らかに結ぶ
[/st-mybox]
このステップで\(y=log_{2}x\)のグラフを書いてみましょう。
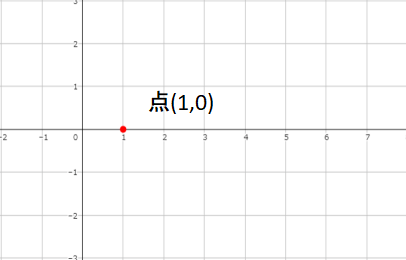
[st-step step_no=”1″]点(1,0)に目印をつける[/st-step]
対数関数のグラフは点(1,0)を通るので目印を付けましょう
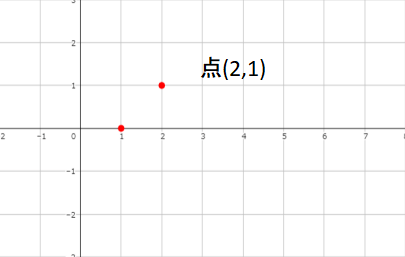
[st-step step_no=”2″]点(a,1)に目印をつける[/st-step]
\(y=log_{2}x\)は\(x=2\)のとき\(y=1\)となります。
なので、点(2,1)にも目印を付けましょう。
[st-step step_no=”3″]y軸を漸近線にして、滑らかに結ぶ[/st-step]
最後に2点(1,0),(2,1)を通るように、滑らかな曲線を書きます。
\(y=log_{2}x\)は\(y\)軸を漸近線とするので、y軸に触れないように気を付けてください。
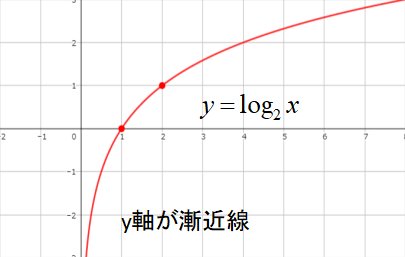
これで対数関数\(y=log_{2}x\)のグラフが完成です。
 高校生
高校生ぼくでも書ける気がします!
漸近線に注意しよう
対数関数のグラフを書くときは、漸近線の存在に注意しましょう。
対数関数\(y=log_{a}x\)のグラフではy軸が漸近線です。
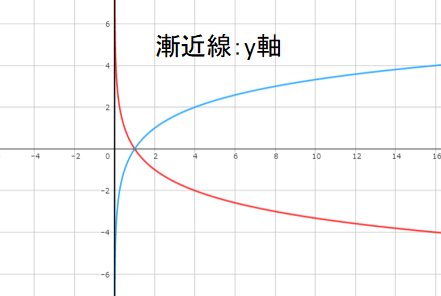
限りなくy軸に近づくようにグラフを書きますが、絶対に漸近線に触れてはいけません。
採点者はこういった細かいところを見ています。
 シータ
シータグラフを書く問題のときは気をつけましょう
対数関数のグラフの移動
対数関数の移動には、主に2つの方法があります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 平行移動
- 対称移動
[/st-mybox]
対数関数に限らず、どのグラフの移動にも応用できるので、ぜひ習得してください。
 高校生
高校生平行移動ってどうやるんだっけ…
平行移動
グラフの形は一切変えずに、一定の方向にそのまま移動させることを平行移動といいます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=log_{a}x\)を\(x\)軸方向に\(p\)、\(y\)軸方法に\(q\)だけ平行移動すると
\[y=log_{a}(x-p)+q\]
[/st-mybox]
\(y=log_{2}x\)のグラフを\(x\)軸方向に\(3\)、\(y\)軸方法に\(-1\)だけ平行移動すると
\[y=log_{2}(x-3)-1\]
となります。
\(y=log_{2}(x-1)-1\)のグラフは下図になります。
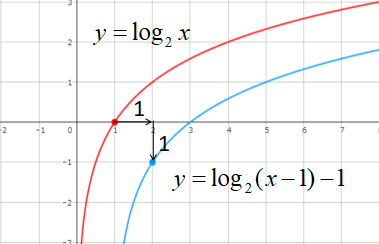
対称移動
原点や直線に対して、元の位置と反対側へ移動させることを対称移動といいます。
[st-mybox title=”対称移動” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
対数関数\(y=log_{a}x\)において、
・\(x\)軸に関して対称移動
\[y=-log_{a}x\]
・\(y\)軸に関して対称移動
\[y=log_{a}(-x)\]
・原点に関して対称移動
\[y=-log_{a}(-x)\]
[/st-mybox]
\(x\)軸に関して\(y=log_{2}x\)を対象移動すると、\(y=-log_{2}x\)のグラフになります。
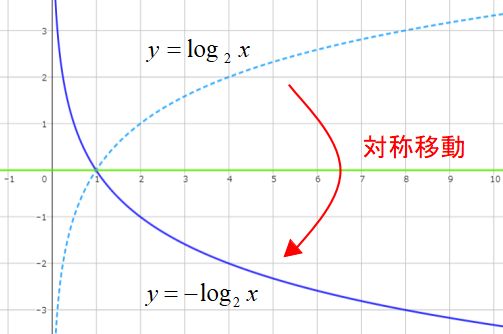
平行移動や対象移動をするときの式変形は、どの関数でも同じような計算をします。
以下の形を覚えておきましょう。
[st-mybox title=”平行移動・対称移動の公式” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
関数\(y=f(x)\)において、
\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動
⇒\(y=f(x-p)+q\)
\(x\)軸に関して対称移動⇒\(y=-f(x)\)
\(y\)軸に関して対称移動⇒\(y=f(-x)\)
原点に関して対称移動⇒\(y=-f(-x)\)
[/st-mybox]
[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#fafafa” align=”” add_style=”margin-bottom:0px; border-top:2px #ccc solid; border-bottom:2px #ccc solid;”]
基礎から丁寧に確認!
プロ講師の分かりやすい解説
[/st-wide-background]
[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#ffffff” align=”” add_style=””]
ここまで読んで、まだピンと来ていない人いますか?
もしかすると、あなたには文章よりも動画解説のほうが合っているかもしれません。

河合塾が提供する「河合塾One」なら解説が丁寧で、基礎から確認できるのでおすすめです。
しかも、いまなら無料体験で全授業が視聴できます。
[/st-wide-background]
対数関数のグラフ《練習問題》
[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#fafafa” align=”” add_style=”margin-top:0px; margin-bottom:0px;”]

対数関数のグラフに関する練習問題に挑戦してみましょう。
以下が今回の練習問題です。
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の対数関数のグラフを書いてみよう。
(1) \(y=log_{3}x\)
(2) \(y=log_{\frac{1}{2}}x\)
(3) \(y=log_{2}(x+1)+2\)
[/st-mybox]
[/st-wide-background]
 シータ
シータ頭の中でグラフの形をイメージしてみよう
練習問題1の解説
[st-mybox title=”練習問題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の対数関数のグラフを書いてみよう。
(1) \(y=log_{3}x\)
[/st-mybox]
底が3で1より大きいので、右上がりのグラフをイメージします。
まずは点(1,0)に目印をつけます。
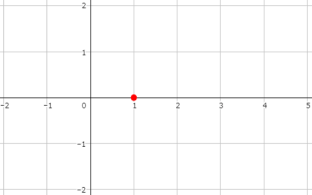
そのあと、底が3なので点(3,1)にも目印をつけましょう。
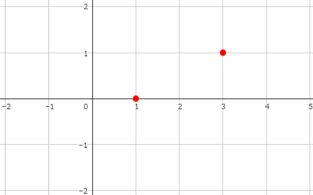
目印をつけた2点を通るように滑らかな曲線を書きます。
このとき漸近線の\(y\)軸に触れないように気を付けましょう。
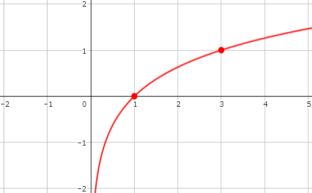
これで\(y=log_{3}x\)のグラフは完成です。
 高校生
高校生グラフにもかなり慣れてきました!
練習問題2の解説
[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の対数関数のグラフを書いてみよう。
(2) \(y=log_{\frac{1}{2}}x\)
[/st-mybox]
底が\(\displaystyle \frac{1}{2}\)で1より小さいので、右下がりのグラフになります。
まず、点(1,0)に目印をつけましょう。
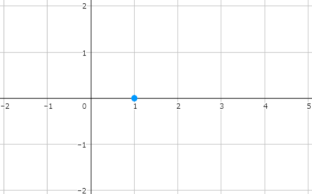
底が1より小さいので、点(2,-1)にも印をつけます。
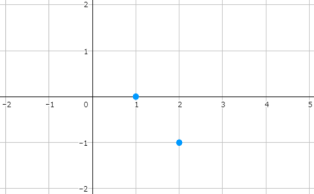
漸近線に気を付けながら、2点を通る曲線を書いたらグラフの完成です。
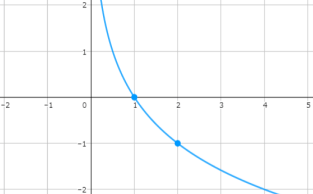
底が1より小さいときのグラフにも慣れておきましょう。
練習問題3の解説
[st-mybox title=”練習問題3″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の対数関数のグラフを書いてみよう。
(3) \(y=log_{2}(x+1)+2\)
[/st-mybox]
この関数は\(y=log_{2}x\)を\(x\)軸方向に-1、\(y\)軸方向に2だけ平行移動したものです。
平行移動したため、通過する点や漸近線が\(y=log_{2}x\)とは異なります。
| x軸との交点 | 点(a,1) | 漸近線 | |
|---|---|---|---|
| \(y=log_{2}x\) | (1,0) | (2,1) | x=0 (y軸) |
| \(y=log_{2}(x+1)+2\) | (0,2) | (1,3) | x=-1 |
通過する点に注意してグラフを書くと以下のようになります。
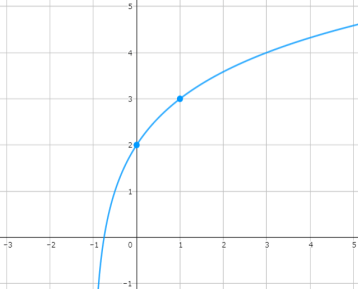
これで\(y=log_{2}(x+1)+2\)のグラフを書くことができました。
対数関数を平行移動する問題は少ないですが、出題されたときにグラフが書けるようにはしておきましょう。
 シータ
シータ知っていれば解けるので差をつけられるよ
対数関数のグラフ まとめ
今回は対数関数のグラフについてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 0 0″ myclass=””]対数関数のグラフ まとめ[/st-marumozi]
[st-mybox title=”対数関数” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1,x>0\)とするとき、以下のような関数を対数関数という。
\[y=log_{a}x\]
[/st-mybox]
対数関数のグラフには以下のような特徴があります。
[st-mybox title=”対数関数のグラフの特徴” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(1,0)を通る
- a>1のとき右上がりで、点(a,1)を通る
- 0<a<1のとき右下がりで、点(\(\displaystyle \frac{1}{a}\),-1)を通る
- y軸が漸近線
[/st-mybox]
グラフを書くときは以下の手順で書きましょう。
[st-mybox title=”対数関数のグラフの書き方” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(1,0)に目印をつける
- a>1ならば点(a,1)に目印を付ける。
0<a<1ならば点(\(\displaystyle \frac{1}{a},-1\))に目印を付ける。 - y軸を漸近線にして、滑らかに結ぶ
[/st-mybox]
今回は対数関数のグラフについて解説しましたが、対数と密接な関係をもつのが指数関数です。
指数関数のグラフの特徴や書き方はこちらの記事で解説しています。
定期テストに向けて指数・対数の復習をするならこちらの記事がおすすめです。
[st-mybutton class=”” url=”https://math-travel.jp/shisuu-log/” title=”指数関数・対数関数のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]

