「数と式の単元が苦手」
「数と式の復習がしたい」
今回は数と式のこんな悩みを全部解決します。
高校生式の展開とかが苦手で…
数学Ⅰ「数と式」の基礎が詰まった「完全攻略」記事を書きました。
「数と式」で学習する内容はこれから習う高校数学の基礎となるものです。
さっそくに高校数学に苦手意識を持っている方も多いと思いますが、じっくり向き合って苦手を解消させておきましょう。
本記事では、数学ⅠAの数と式について徹底解説します。
長い記事ですがゆっくり読めば数と式の総復習ができるようになっています。
数と式
単項式と多項式
まず単項式と多項式の定義を確認します。
単項式
数や文字およびそれらを掛けただけで表される式
例）5,xy,2a,(-3abc)
多項式
単項式の和として表される式
例）x+y ,2ab-3a+b
つまり、多項式はいくつかの単項式をもっている式です。
また、単項式と多項式はどちらも整式の1つです。
単項式と多項式の違いについて詳しく知りたい方
⇒単項式と多項式の違い
同類項でまとめる
同じ文字をもつ項を同類項と呼びます。
同類項をまとめるとは「整式の同じ文字を持つ項を1つにまとめること」を指します。
同類項のまとめ方は別の記事で詳しく解説しています。
⇒同類項でまとめるとは？整式の整理を解説！
指数法則
指数法則を理解していないと、式の展開などで苦戦します。
指数法則には覚えておきたい7つの公式があります。
指数法則の７つの公式
- \(a^{0}=1\)
- \(\displaystyle a^{-n}=\frac{1}{a^{n}}\)
- \(a^{m} \times a^{n}=a^{m+n}\)
- \((a^{m})^{n}=a^{mn}\)
- \((ab)^{n}=a^{n} b^{n}\)
- \(a^{m} \div a^{n}=a^{m-n}\)
- \(\displaystyle (\frac{a}{b})^{n}=\frac{a^{n}}{b^{n}}\)
なぜこのようになるのかは別記事で解説しています。
⇒分数やマイナスにも困らない指数法則の7つの公式
展開の公式
展開の公式は完璧に覚える必要はありません。しかし、自力で計算できるくらいには理解しておきましょう。
3次式の展開
3次式の展開公式について解説します。
(a±b)^{3}の展開公式
\((a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\)
\((a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\)
上で示したように、3乗の展開は少し複雑です。
3次式の展開公式について詳しく知りたい方
3次式の展開公式を徹底解説！
(a±b)3乗の展開公式 証明
\((a±b)^{3}\)の展開公式を証明していきましょう。
証明は計算していくだけなのでかなりシンプルです。
・\((a+b)^{3}\)の証明
\begin{eqnarray}
(a+b)^{3}&=&(a+b)^{2}(a+b)\\
&=&(a^{2}+2ab+b^{2})(a+b)\\
&=&a^{3}+3a^{2}b+3ab^{2}+b^{3}\\
\end{eqnarray}
・\((a-b)^{3}\)の証明
\begin{eqnarray}
(a-b)^{3}&=&(a-b)^{2}(a-b)\\
&=&(a^{2}-2ab+b^{2})(a-b)\\
&=&a^{3}-3a^{2}b+3ab^{2}-b^{3}\\
\end{eqnarray}
上の2つの式は素直に展開していくと展開公式が出てきます。
3次式の因数分解
次は3次式の因数分解について解説します。
公式を見ながら練習していけば段々できるようになります。
\((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
\((a+b)(a^2-ab+b^2)=a^3+b^3\)
\((a-b)(a^2+ab+b^2)=a^3-b^3\)
実数とは
実数とは「有理数」と「無理数」の総称です。
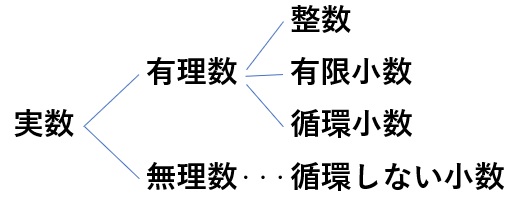
多くの高校生が「有理数」と「無理数」の違いに困ると思います。
有理数というのは、分数で表現できる数を指しています。具体的には、以下のように「整数」「有限小数」「循環小数」が含まれています
一方で、無理数とは\(\sqrt{3}\)や\(\pi\)などの循環しない数のことです。
\(\sqrt{3}=1.7320508…\)
\(\pi =3.141592…\)
もっと詳しく知りたい方はこちら
⇒実数とは？ルートは実数？実数の定義を解説！
2重根号の計算
二重根号の外し方を伝授していきます。
外し方法はとっても簡単！
この公式を覚えていれば、問題なしです。
命題と条件
命題とは「正しいか正しくないかが１つに定まる文章または式」を指します。
命題の例
- \(x=3\)ならば\(2x=6\)である
- 4は偶数である
- ライオンは生き物である
一方で、以下のような文章は命題とは言えません。
命題ではない例
- 1000は大きい数である
- 車は速い
- 東京はすごい
なぜなら、大きいや速いというのは比べるものによって変わる概念だからです。
このような正しい正しくないが明確に決められない文章や式を命題とは言えません。
命題と合わせて「逆・裏・対偶」についても解説しているのでぜひご覧下さい。
⇒命題とは？命題の意味と「逆・裏・対偶」の関係
必要条件・十分条件
まず、必要条件・十分条件の定義を確認しましょう。
高校生pとかqで説明されても分からないよ
シータそうだよね。
具体的な命題で解説していくよ
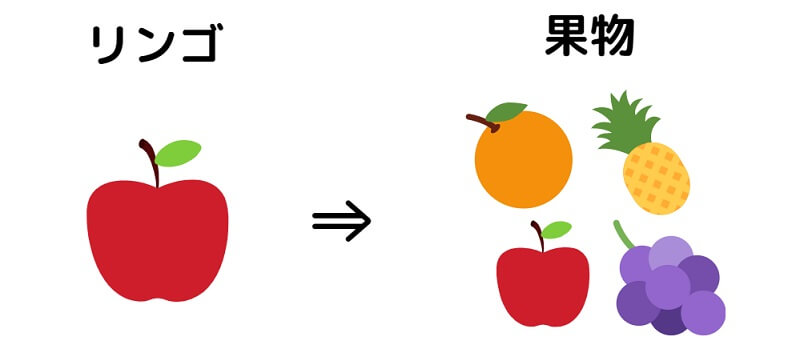
真の命題「リンゴならば果物」を例にして考えます。
「リンゴならば果物である」という命題を矢印で表すと「リンゴ⇒果物」です。
ポイント
- 矢印が出ているほうが十分条件
- 矢印を受けているほうが必要条件
つまり、リンゴ⇒果物 において
- 「リンゴ」は「果物」の十分条件
- 「果物」は「リンゴ」の必要条件
ここで注意点が1つ
命題が逆になると必要条件・十分条件も逆になります。
つまり、「\(x=1\)」は「\(x+3=4\)」の十分条件でもあり、必要条件でもあります。
このような場合、「\(x=1\)」は「\(x+3=4\)」の必要十分条件といいます。
高校生矢印が出ている方が十分条件なんだね
命題の必要条件・十分条件について詳しく知りたい方
必要条件・十分条件とは？違いと見分け方を分かりやすく解説！
数と式 まとめ
今回は数と式についてまとめました。
数と式の記事を網羅的にまとめましたが、詳しいポイントは各単元の記事で解説しています。
そちらもぜひ参考にしてください。
数と式
数と式以外の単元についてもまとめ記事を出しています。
まとめ記事
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように！
コメント