同類項でまとめるとは？整式の整理を解説！

今回は同類項に関する疑問を解決していきます。

単項式と多項式を学習すると、「同類項をまとめなさい」という問題が出ます。

同類項をまとめるってどういうことだろう？

今回は整式の整理の中から、同類項のまとめ方について解説します。

本記事でしっかりと理解しておきましょう！

同類項をまとめるとは？

単項式と多項式を習うと、次は整式の整理に入ります。

整式の項の中で、文字の部分が同じ項を同類項といいます。

同類項をまとめるとは、「整式に含まれる同類項を計算し1つにすること」を指します。

同類項のまとめ方

同類項のまとめ方を解説します。

同類項のまとめ方は決して難しくないので安心してください。

整式の中に同類項がないか確認します。

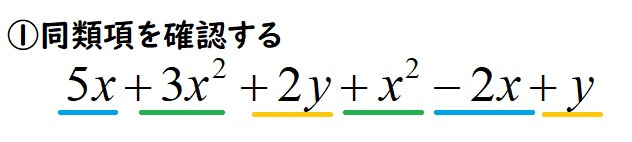
同類項の係数を計算します。

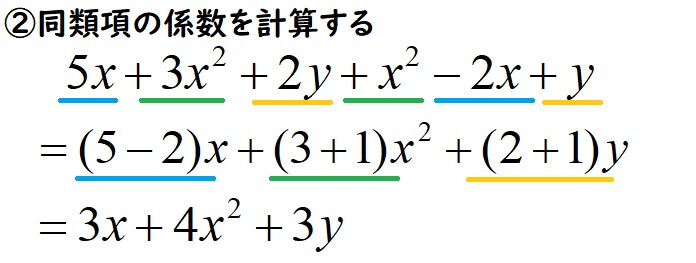
計算は以上ですが、次数が下がっていくように並び変えます。
次数が下がっていく並び方を降べきの順と呼びます。

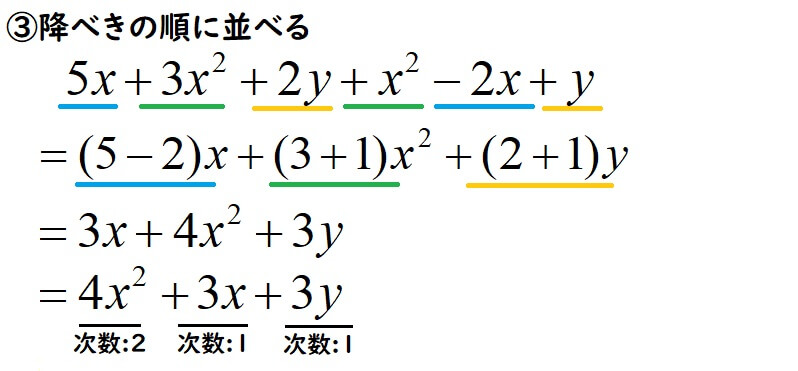
これで同類項をまとめることができました。

整式の次数

同類項をまとめた整式において、最も高い次数をその整式の次数とします。

また、次数がn次の整式をn次式という。

例：\(4x^2+3x+3y\)の最高の次数は2で、2次式である。
\(5x^3+2x^2-3x+6\)の最高の次数は3で、3次式である。

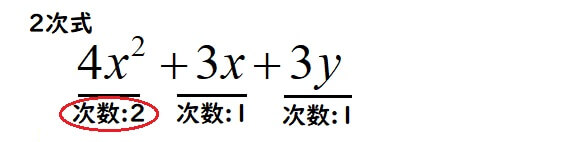
同類項　まとめ

今回は整式の整理から同類項についてまとめました。

他にも、教科書に内容に沿った解説記事を挙げています。

お気に入り登録して定期試験前に確認してください。

最後まで読んでくださりありがとうございました。

みんなの努力が報われますように！