[mathjax]
「指数関数・対数関数が苦手」
「指数・対数の総復習がしたい」
今回は指数関数と対数関数に関するこんな悩みを解決します。
 高校生
高校生テストに向けて指数・対数の復習がしたいです…
本記事では指数・対数関数について徹底解説しています。
ぜひ定期テストに向けた総復習に活用してください。
[st_af id=”13740″]
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
指数関数
指数関数とは、\(a>0,a≠1\)として\(y=a^{x}\)のように指数に変数を含む関数です。
[st-mybox title=”指数関数” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)のとき
\[y=a^{x}\]
[/st-mybox]
\(y=a^{x}\)において、\(a\)のことを底(てい)といい、\(x\)のことを指数(しすう)と呼びます。
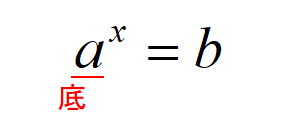
つまり、\(y=a^{x}\)は「底が\(a\),指数\(x\)の指数関数」ということですね。
指数関数のグラフはどんな形?
指数関数のグラフをイメージできますか?
底の値によって、指数関数のグラフは変化するので注意しましょう。
[1] \(a>1\)のとき
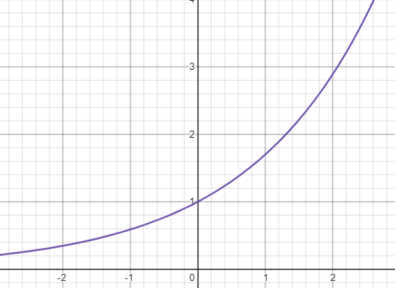
[st-mybox title=”a>1のとき” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど増加
- \(x\)が小さくなるほど0に近づく
[/st-mybox]
[2] \(a<1\)のとき
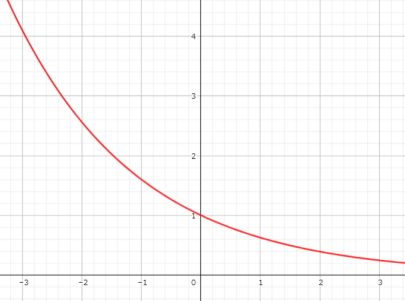
[st-mybox title=”a<1のとき” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど0に近づく
- \(x\)が小さくなるほど増加
[/st-mybox]
指数関数のグラフの書き方はこちらでまとめました。
⇒対数関数のグラフと書き方3ステップを解説!
指数の計算公式
指数関数を使いこなすには指数法則の理解も欠かせません。
以下が指数法則の重要な公式です。
[st-mybox title=”指数法則の基本公式” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a≠0,b≠0\)で、\(m,n\)が整数のとき
- \(a^{m} \times a^{n}=a^{m+n}\)
- \((a^{m})^{n}=a^{mn}\)
- \((ab)^{n}=a^{n}b^{n}\)
- \(a^{m} \div a^{n}=a^{m-n}\)
- \(\displaystyle \left(\frac{a}{b} \right)^{n}=\frac{a^{n}}{b^{n}}\)
[/st-mybox]
以下の3つの公式もかなり重要です。
[st-mybox title=”指数法則の重要公式” fontawesome=”fa-check-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a≠0,b≠0\)で、\(m,n\)が整数のとき
- \(a^{0}=1\)
- \(\displaystyle a^{-n}=\frac{1}{a^{n}}\)
- \(\displaystyle a^{\frac{1}{n}}=\sqrt[n]{a}\)
[/st-mybox]
ここでは公式の紹介しかしませんが、詳しい使い方や練習問題は「指数法則の重要な公式8選!これで分数やマイナスにも困らない!」で解説しています。
指数方程式
以下のような指数関数を含む方程式を指数方程式といいます。
[st-mybox title=”指数方程式の例” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[2^{x}=8\]
\[9^{x}+3^{x}=90\]
\[2^{2x}-6 \cdot 2^{x} +8=0\]
[/st-mybox]
方程式を解くというのは、与えられた等式を成り立たせる\(x\)の値を求めることを指します。
指数方程式の解き方には大きく5つパターンがあります。
[st-mybox title=”指数方程式の5パターン” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 底をそろえる問題
- ルートや分数がある問題
- 置き換える問題
- 対数で答える問題
- 連立方程式の問題
[/st-mybox]
それぞれの解き方は「指数方程式の解き方!全5パターンを分かりやすく解説!」にて解説しました。
指数不等式
指数方程式の次は指数不等式です。
以下のような指数に変数\(x\)を含む不等式を指数不等式といいます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\begin{eqnarray}
2^{x}&≧&8\\
\displaystyle \left(\frac{1}{3}\right)^{x+1}&<&\left(\frac{1}{9}\right)^{x}
\end{eqnarray}
[/st-mybox]
指数不等式を解くときには底\(a\)の値に注意しましょう。
[st-mybox title=”注意ポイント” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)において
\(a>1\)のとき、\(y=a^{x}\)は増加関数なので
\[a^{m}<a^{n} \Leftrightarrow m<n\]
\(0<a<1\)のとき、\(y=a^{x}\)は減少関数なので
\[a^{m}<a^{n} \Leftrightarrow m>n\]
[/st-mybox]
指数不等式にも解き方があり、「指数不等式の解き方と注意点!logや置き換え問題も解説!」にて解き方を詳しく解説しています。
[st-mybox title=”指数不等式のパターン” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 底が1より大きいとき
- 底が1より小さいとき
- 置き換える問題
- 対数をとる問題
[/st-mybox]
対数関数
\(y=log_{a}x\)のような関数を、\(a\)を底とする\(x\)の対数関数といいます。
[st-mybox title=”対数関数” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1,x>0\)とするとき、以下のような関数を対数関数という。
\[y=log_{a}x\]
[/st-mybox]
対数logとは?
対数\(log_{a}M\)とは、「\(M\)は\(a\)の何乗なのか」を表したものです。
[st-mybox title=”対数” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)で\(M>0\)において、
\[log_{a}M=x \Leftrightarrow a^{x}=M\]
ただし、真数\(b\)は正の数である。
[/st-mybox]
\[a^{x}=M\]
\(a\)の\(x\)乗が\(M\)のとき、対数で表すことで
\[log_{a}M=x\]
と表されます。
 シータ
シータ指数と対数は合わせて理解していこう
\(log_{a}b=x\)における\(a\)を底(てい)、\(b\)を真数(しんすう)といいます。

底は指数で表すときにも使う用語なので覚えておきましょう。
指数\(a^{x}=b\)における\(a\)を底、\(x\)を指数といいます。
対数の性質
指数に指数法則があるように、対数にもいくつか重要な性質があります。
[st-mybox title=”対数の性質” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,m>0,n>0,a≠1\)において
\(log_{a}a=1\)
\(log_{a}a^{m}=m\)
\(log_{a}b^{m}=m log_{a}b\)
\(log_{a}m+log_{a}n=log_{a}mn\)
\(\displaystyle log_{a}m-log_{a}n=log_{a} \frac{m}{n}\)
[/st-mybox]
これらの性質は対数の計算で当たり前のように使います。
底の変換公式
底の変換公式は対数logの重要な公式の1つです。
[st-mybox title=”底の変換公式” fontawesome=”fa-exclamation-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a,b,c>0、a,c≠1\)のとき
\[\displaystyle log_{a}b=\frac{log_{c}b}{log_{c}a}\]
[/st-mybox]
以下のような対数の計算があったとしましょう。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の計算を求めよう。
\[\displaystyle log_{2}3 \cdot log_{3}4\]
[/st-mybox]
これらは対数の底が異なるので、このままでは積を求めることができません。
そこで底の変換公式の出番です。
\[\displaystyle log_{3}4=\frac{log_{2}4}{log_{2}3}=\frac{2}{log_{2}3}\]
底の変換公式を使えば、底を計算の都合がよい値に変換することができるのです。
この問題では、対数の底を2に変換して積を求めましょう。
\begin{eqnarray}
\displaystyle log_{2}3 \cdot log_{3}4&=&log_{2}3 \cdot \frac{2}{log_{2}3}\\
&=&2
\end{eqnarray}
このように底の変換公式を用いることで、対数の計算がスムーズにできるようになります。
非常に重要な公式なので必ず覚えておきましょう。

底の変換公式については、「底の変換公式について解説!証明と底を決めるコツが分かる!」にて詳しく解説しています。
対数関数のグラフ
対数関数のグラフの形について考えていきましょう。
対数関数をグラフで表すときは、底の値に注意が必要です。
\(a>1\)のときは、右上がりのグラフになります。
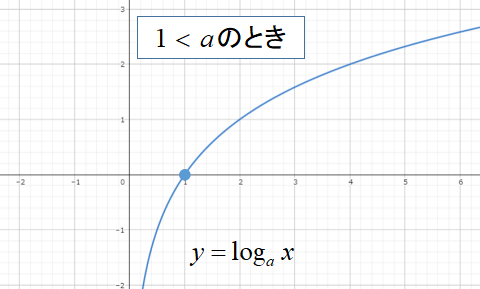
\(0<a<1\)のときは、右下がりのグラフになります。
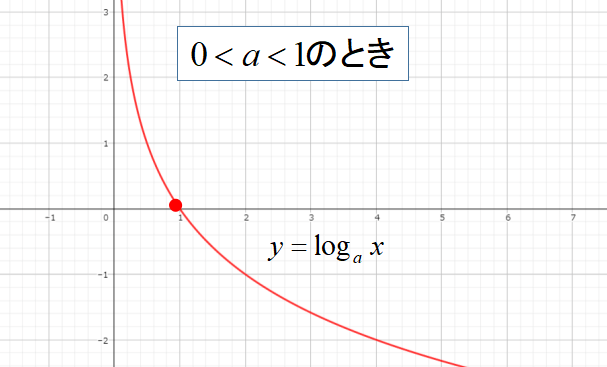
 高校生
高校生滑らかな曲線になるんですね!
対数関数のグラフの特徴をまとめました。
[st-mybox title=”対数関数のグラフの特徴” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(1,0)を通る
- a>1のとき右上がりで、点(a,1)を通る
- 0<a<1のとき右下がりで、点(\(\displaystyle \frac{1}{a}\),-1)を通る
- y軸が漸近線
[/st-mybox]
対数関数のグラフのポイントや書き方は「対数関数のグラフと書き方3ステップを解説!」で解説しています。
対数関数の方程式
対数関数を含む以下のような方程式を対数方程式といいます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[log_{2}x=3\]
\[log_{4}x+log_{4}(x-6)=2\]
[/st-mybox]
この方程式を成り立たせる\(x\)を求めるのが、対数方程式の主な問題です。
方程式が長くなると難しく見えますね。
 高校生
高校生そうです。こういうのが苦手なんです..
対数方程式を解くには、以下の形を目指して式変形をしていきます。
[st-mybox title=”対数方程式の解き方” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)で、\(M>0,N>0\)のとき
\[log_{a}M=log_{a}N\]
ならば
\[M=N\]
[/st-mybox]
つまり、
\[log_{2}x=log_{2}5⇒x=5\]
というわけです。
とはいえ、こんな簡単な問題はそうそうありません。
どんな対数方程式の問題でも、以下の5ステップで解を求めることができます。
[st-mybox title=”対数方程式の解き方” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 真数条件と底の条件を確認
- 両辺の底を同じにする
- 真数をイコールでむすぶ
- 方程式を解く
- 解と条件を確認して完了
[/st-mybox]
また、対数方程式の問題は以下の4種類に分けることができる。
[st-mybox title=”対数方程式の問題” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 基本の問題
- 底をそろえる問題
- 置き換える問題
- 底に文字を含む問題
[/st-mybox]
対数関数の不等式
対数関数を含む不等式を対数不等式といいます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[log_{2}x>3\]
\[2log_{3}(2-x)<log_{3}(x+4)\]
[/st-mybox]
この不等式を満たす\(x\)の変域を求めます。
対数不等式を解くときは、真数条件と底\(a\)の値に注意しましょう。
[st-mybox title=”真数条件” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(y=log_{a}x\)において、真数\(x\)は正の数である。
[/st-mybox]
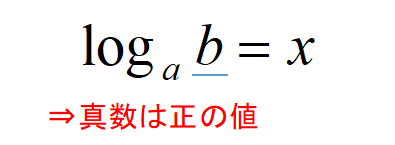
\(b\)の部分が正であることは必ず確認するようにしましょう。
また、真数条件とあわせて、底\(a\)の値にも注意しましょう。
[st-mybox title=”注意ポイント” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0.a≠1,x>0\)において、
\(a>1\)ならば、\(y=log_{a}x\)は増加関数なので
\[log_{a}m<log_{a}n \Leftrightarrow m<n\]
\(0<a<1\)ならば、\(y=log_{a}x\)は減少関数なので
\[log_{a}m<log_{a}n \Leftrightarrow m>n\]
[/st-mybox]
\(a>1\)のときは、グラフが右肩上がりなので\(log_{a}m<log_{a}n\)のとき、\(m<n\)が成り立ちます。
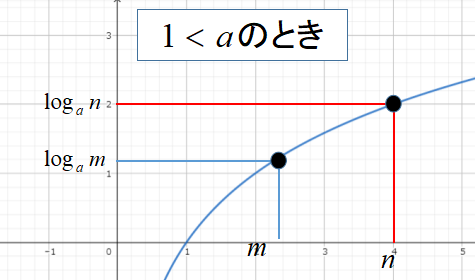
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>1\)のとき、
\[alog_{a}m<log_{a}n \Leftrightarrow m<n\]
[/st-mybox]
しかし、\(0<a<1\)のときはグラフの右肩下がりになるので不等号の向きが逆になります。
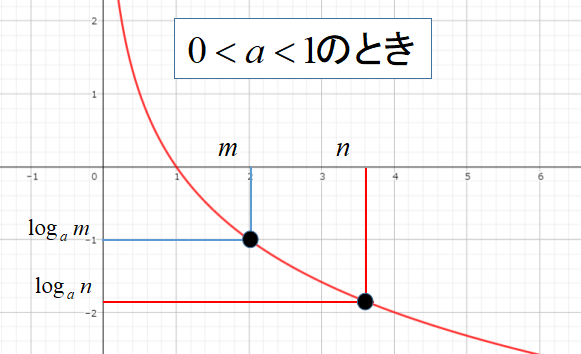
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(0<a<1\)のとき、
\[log_{a}m<log_{a}n \Leftrightarrow m>n\]
[/st-mybox]
不等式を解いたら、\(a\)の値と不等号の向きをチェックしましょう。
かなり重要なことなので、対数不等式が苦手な方は以下の記事を必ず読むようにしてください。
おすすめ動画
《とある男が授業をしてみた》
【2次関数・2次方程式・2次不等式】再生リスト
指数関数・対数関数 まとめ
今回は指数関数・対数関数を総復習できるように網羅的にまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]指数・対数 まとめ[/st-marumozi]
指数関数とは、\(a>0,a≠1\)として\(y=a^{x}\)のように指数に変数を含む関数です。
[st-mybox title=”指数関数” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)のとき
\[y=a^{x}\]
[/st-mybox]
\(y=a^{x}\)において、\(a\)のことを底(てい)といい、\(x\)のことを指数(しすう)と呼びます。
\(y=log_{a}x\)のような関数を、\(a\)を底とする\(x\)の対数関数といいます。
[st-mybox title=”対数関数” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1,x>0\)とするとき、以下のような関数を対数関数という。
\[y=log_{a}x\]
[/st-mybox]
\(log_{a}x\)の\(a\)の部分を底(てい)、\(x\)の値を真数(しんすう)といいます。

指数関数・対数関数に苦手意識を持っている人は多いです。
しかし、覚える公式は少ない単元なので、基本を正しく理解すれば点数が取れるようになります。
指数・対数以外の単元についてもまとめ記事を出しています。
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

