指数方程式の解き方！全5パターンを分かりやすく解説！

「指数方程式の解き方が分からない」
「ルートや分数があって困っている」
今回は指数方程式に関するこんな悩みを解決します。

以下のような指数に変数\(x\)を含む方程式を指数方程式といいます。

見た目が難しそうなので、解く前から苦手意識が湧いてきますよね。

実は指数方程式の問題は、大きく5つのパターンに分けることができます。

この5パターンの解き方さえ理解しておけば、大体の問題は解けるようになるでしょう。

本記事では指数法則の解き方全5パターンを解説します。

例題を交えながら解説していくので、ぜひ最後までご覧ください。

※本ページは学習アプリのプロモーションが含まれています。

指数関数とは？

指数方程式の前に指数関数について確認しておきましょう。

指数関数とは、\(a>0,a≠1\)において\(y=a^{x}\)と表される関数です。

以下は\(a>1\)における指数関数\(y=a^{x}\)のグラフです。

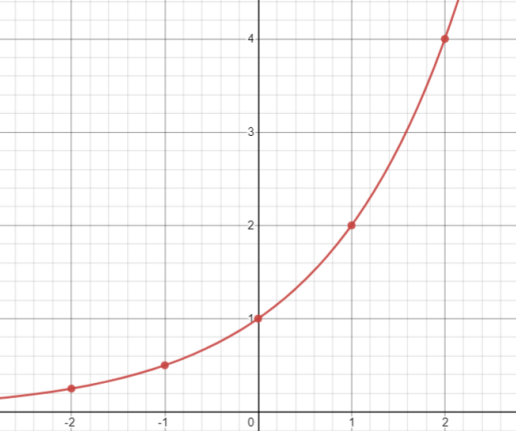
指数関数のグラフから分かるように、\(a^{x}=y\)を満たす\(x\)はただ1つに定まります。

つまり、指数方程式の解もただ1つに定まることになりますね。

指数方程式

以下のような指数関数を含む方程式を指数方程式といいます。

方程式を解くというのは、与えられた等式を成り立たせる\(x\)の値を求めることを指します。

指数方程式の解き方

指数方程式の問題は大きく5つのパターンしかありません。

問題にパターンがあるということは、解き方を覚えれば解ける問題がグッと広がります。

この問題のときはどうするのか、そういったアプローチの仕方を理解していきましょう。

底をそろえる問題

まずは1番シンプルな問題から紹介します。

この問題は両辺の底を揃えることで、指数を比較して解を求めます。

両辺を底が同じ累乗で表すことを目標に考えましょう。

\begin{eqnarray}
2^{x}&=&8\\
2^{x}&=&2^{3}\\
x&=&3
\end{eqnarray}

(2)は両辺を底3の累乗に直すと解を求めることができます。

\begin{eqnarray}
9^{x}&=&27\\
(3^{2})^{x}&=&3^{3}\\
3^{2x}&=&3^{3}\\
2x&=&3\\
\displaystyle x&=&\frac{3}{2}
\end{eqnarray}

式変形の途中に指数法則を使った計算がありましたね。

「何が起こった！？」

そう思った人もいるかもしれませんが、指数法則は当たり前のように使われます。

指数の計算が不安なひとは、指数法則の重要公式を確認しましょう。
⇒指数法則の重要な公式8選！これで分数やマイナスにも困らない！

ルートや分数がある問題

ルートや分数の指数計算が苦手なひとも多いですよね。

(1)は両辺を底2の累乗に直しましょう。

\begin{eqnarray}
\displaystyle 8^{x}&=&\frac{1}{16}\\
\displaystyle 2^{3x}&=&\frac{1}{2^{4}}\\
2^{3x}&=&2^{-4}\\
3x&=&-4\\
\displaystyle x&=&-\frac{4}{3}
\end{eqnarray}

(2)はルートがありますね。
ルートは指数が分数の累乗にすることができます。

\begin{eqnarray}
2^{1-x}&=&\sqrt[3]{2}\\
\displaystyle 2^{1-x}&=&2^{\frac{1}{3}}\\
\displaystyle 1-x&=&\frac{1}{3}\\
\displaystyle x&=&\frac{2}{3}\\
\end{eqnarray}

ルートや分数に関係する指数法則も確認しましょう。

置き換える問題

指数方程式にはこんな長い問題もあります。

この指数方程式は\(2^{x}\)を\(t\)に置き換えると解きやすくなります。

\begin{eqnarray}
t^{2}-6t+8&=&0\\
(t-2)(t-4)&=&0\\
t&=&2,4
\end{eqnarray}
\(t\)を\(2^{x}\)に戻して、
\begin{eqnarray}
2^{x}&=&2,4\\
x&=&1,2
\end{eqnarray}

これは解き方を知らないと苦戦する問題ですね。

対数をとる問題

両辺を同じ底では表せない問題もあります。

同じ底で表せないときは、両辺の対数をとりましょう。

この問題の場合は、\(log_{2}\)にすると計算しやすいです。

\begin{eqnarray}
2^{x}&=&5\\
log_{2}2^{x}&=&log_{2}5\\
x log_{2}2&=&log_{2}5\\
x&=&log_{2}5
\end{eqnarray}

(2)の問題も見てみましょう。

\begin{eqnarray}
3^{x}&=&12\\
log_{3}3^{x}&=&log_{3}12\\
x log_{3}3&=&log_{3}(3 \cdot 4)\\
x&=&log_{3}3+log_{3}2^{2}\\
x&=&1+2 log_{3}2
\end{eqnarray}

連立方程式の問題

最後のパターンは連立方程式をつかって考えます。

これは\(3^{x}=X,5^{y}=Y\)に置き換えることで、連立方程式として考えます。

\begin{eqnarray}
2 \cdot X+Y&=&79 \\
X+2 \cdot Y&=&77
\end{eqnarray}

これを解くことによって、

\[X=27,Y=25\]

したがって、

\[3^{x}=27,5^{y}=25\]

\[∴ x=3,y=2\]

指数方程式《練習問題》

5つの指数方程式の解き方を使って練習問題にチャレンジしてみましょう。

練習問題1の解説

この問題は分数とルートがあるので難しそうに見えますが、底をそろえて解いていきます。

\begin{eqnarray}
\displaystyle \left(\frac{1}{2} \right)^{x-1}&=&(\sqrt{2})^{x}\\
\displaystyle (2^{-1})^{x-1}&=&(2^{\frac{1}{2}})^{x}\\
\displaystyle 2^{1-x}&=&2^{\frac{1}{2} x}\\
\displaystyle 1-x&=&\frac{1}{2}x\\
\displaystyle x&=&\frac{2}{3}
\end{eqnarray}

これで方程式を解くことができました。

解き方を忘れてしまった方は、底をそろえる問題の解き方に戻って復習しましょう。

練習問題2の解説

この問題はいったん違う文字に置き換える問題でしたね。

今回は\(3^{x}\)を\(t\)に置き換えて考えましょう。

\begin{eqnarray}
9^{x}-10 \cdot 3^{x}+9&=&0\\
3^{2x}-10 \cdot 3^{x}+9&=&0\\
t^{2}-10t+9&=&0\\
(t-1)(t-9)&=&0\\
t&=&1,9\\
\end{eqnarray}

\(t\)が求まったところで、\(t\)を\(3^{x}\)に戻します。

\begin{eqnarray}
3^{x}&=&1,9\\
3^{x}&=&3^{0},3^{2}\\
x&=&0,2
\end{eqnarray}

計算をしやすくするために、何を文字に置き換えるかがポイント！

置き換える問題の確認をしたい方は、置き換える問題の解き方を再チェック！

練習問題3の解説

これは両辺の底をそろえて表すことができないので、対数をとって考えます。

\begin{eqnarray}
3^{x}&=&7^{x+1}\\
log_{3}3^{x}&=&log_{3}7^{x+1}\\
x&=&(x+1)log_{3}7\\
(1-log_{3}7)x&=&log_{3}7\\
\displaystyle x&=&\frac{log_{3}7}{1-log_{3}7}
\end{eqnarray}

この問題は\(log_{3}\)ではなく、\(log_{7}\)で対数をとっても方程式を解くことができます。

この問題が不安な方は、対数をとる解き方をもう1度確認しておくと良いでしょう。

指数方程式の解き方　まとめ

今回は指数方程式の解き方についてまとめました。

指数方程式　まとめ

指数方程式の解き方5パターン

指数方程式はもっと複雑な問題を作ることもできますが、基本的な考え方は今回紹介した5つで十分です。

指数方程式を解くにあたって、指数法則と対数法則はよく使うので理解しておきましょう。

指数関数・対数関数について様々な解説をしています。

少しでもに苦手意識がある方はぜひ他の記事もご覧ください。

指数関数・対数関数のまとめ記事へ