[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=””]
「指数関数ってなに?」
「指数関数のグラフってどんな形?」
[/st-mybox]
今回は指数関数に関する悩みを解決するよ。
 高校生
高校生指数関数ってどんな関数だっけ…
\(y=a^{x}\)のような関数を指数関数といいます。
ただし、\(a>0,a≠1\)に限るので\(a\)の値に注意しましょう。
[st-mybox title=”指数関数” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)のとき
\[y=a^{x}\]
[/st-mybox]
指数関数は微分や積分にもつながる単元なのでしっかり押さえておきましょう。
本記事では指数関数について解説しました。
さまざまなグラフを用いて解説するので、指数関数のグラフがイメージできるようになります。
[st_af id=”13740″]
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
指数関数とは?
指数関数とは、\(a>0,a≠1\)として\(y=a^{x}\)のように指数に変数を含む関数です。
[st-mybox title=”指数関数” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)のとき
\[y=a^{x}\]
[/st-mybox]
\(y=a^{x}\)において、\(a\)のことを底(てい)といい、\(x\)のことを指数(しすう)と呼びます。
つまり、\(y=a^{x}\)は「底が\(a\),指数\(x\)の指数関数」ということですね。
[st-mybox title=”そもそも関数とは?(復習)” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
変数\(x,y\)において、片方の変数を1つに決めると、もう一方の変数も1つに定まるもの。
\(y=3^{x}\)の場合、\(x=1\)とすると、\(y=3\)と定まるので関数だといえます。
[/st-mybox]
 シータ
シータ指数関数をグラフで解説するよ
指数関数のグラフ
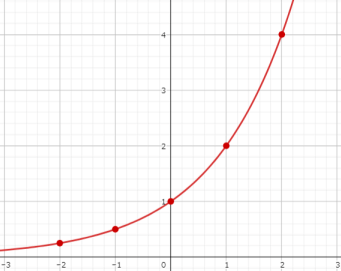
指数関数がどんな関数なのかをグラフを使いながら解説します。
指数関数のグラフは滑らかな形をしているのが特徴です。
 シータ
シータ指数関数のグラフがイメージできるようになろう!
指数関数\(y=2^{x}\)のグラフ
まず、指数関数\(y=2^{x}\)のグラフを見ていきましょう。
\(y=2^{x}\)のグラフは右肩上がりのグラフになります。
\(x\)の値が大きくなるほど、\(y\)の値も大きくなっていますね。
実際に計算しても、\(x\)が大きくなるほど\(y\)の増加量も増加しているのが分かります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\begin{eqnarray}
2^{0}&=&1\\
2^{1}&=&2\\
2^{2}&=&4\\
2^{3}&=&8
\end{eqnarray}
[/st-mybox]

また、\(x\)の値が小さくなるほどx軸に近づいていますね。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\begin{eqnarray}
\displaystyle 2^{-1}&=&\frac{1}{2}\\
\displaystyle 2^{-2}&=&\frac{1}{4}\\
\displaystyle 2^{-3}&=&\frac{1}{8}\\
\displaystyle 2^{-4}&=&\frac{1}{16}
\end{eqnarray}
[/st-mybox]
指数がマイナスのときは、逆数の累乗になることも覚えておきましょう。
[st-mybox title=”指数法則” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a≠0\)で、nが整数のとき
\[\displaystyle a^{-n}=\frac{1}{a^{n}}\]
[/st-mybox]
 シータ
シータ忘れやすい計算だから必ず覚えておこう!
[st-mybox title=”関連記事” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
指数法則の重要公式についてはこちら
⇒指数法則の重要な公式8選!これで分数やマイナスにも困らない!
[/st-mybox]
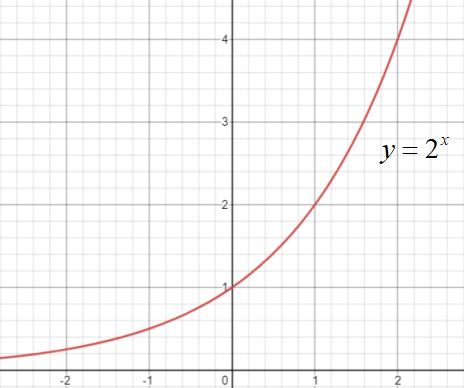
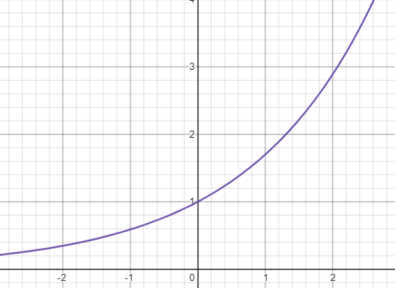
指数関数\(y=a^{x}\)のグラフ
\(a>1\)のとき、\(y=a^{x}\)のグラフは以下のようになります。
[st-mybox title=”a>1のとき” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど増加
- \(x\)が小さくなるほど0に近づく
[/st-mybox]
\(y=2^{x}\)のグラフと形が似ていることが分かりますね。
左に行くほど0に近づき、右に行くほどグングン上に上がっています。
 シータ
シータaの値が大きいほど、上がり方も激しくなるよ
指数の底が1より小さいとき
ここまで\(a>1\)のときのグラフを見てきました。
では、指数関数の底\(a\)が1より小さい時はどうなるのでしょうか?
 高校生
高校生aが1より小さいとグラフが変わるの?
底が\(a<1\)のとき、\(y=a^{x}\)のグラフは以下のようになります。
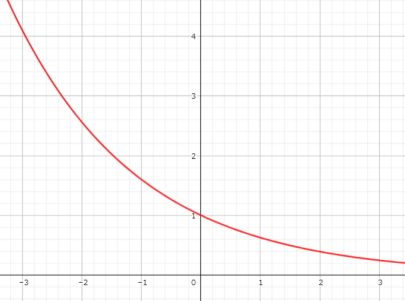
[st-mybox title=”a<1のとき” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど0に近づく
- \(x\)が小さくなるほど増加
[/st-mybox]
先ほど紹介した\(a>1\)のときと比べると、グラフの形が左右対称ですね。
 高校生
高校生右に行くほど0に近づいてる!
 シータ
シータそうなんだよ!aの値によってグラフの形が変わるから注意!
指数関数のグラフの書き方
指数関数のグラフの書き方を解説します。
グラフの書き方は簡単で、以下のステップで書いてみましょう。
[st-mybox title=”指数関数のグラフの書き方” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 分かりやすい通過点に目印を付ける
- a>1ならば右肩上がり、a<1ならば右肩下がりで点をつなぐ
[/st-mybox]
例として\(y=2^{x}\)のグラフを書きます。
 シータ
シータ実際にやってみたよ!
通過点に目印を付ける
まずは\(y=2^{x}\)の通過点に目印を付けます。

| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/4 | 1/2 | 1 | 2 | 4 |
点をなめらかにつなぐ
目印を付けた点をなめらかにつないだら、指数関数のグラフの完成です。
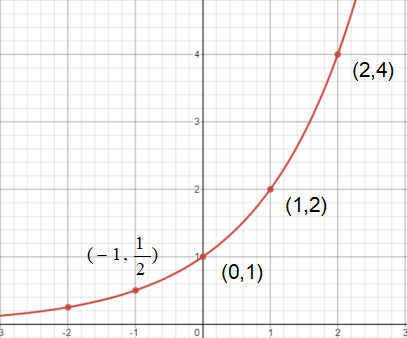
 高校生
高校生直線や放物線を書く手順と同じだね
注意するポイント
グラフを書く際の注意ポイントをまとめました。
[st-mybox title=”注意ポイント” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(0,1)を必ず通ること
- x軸を超えることはない
[/st-mybox]
指数関数のグラフを書くときはこの2つを気を付けよう!
点(0,1)を必ず通ること
\(y=a^{x}\)において、\(a\)の値に関わらず\(x=0\)のとき\(y=1\)になります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[a^{0}=1\]
[/st-mybox]
つまり、どんな指数関数のグラフでも点(0,1)通るのです。
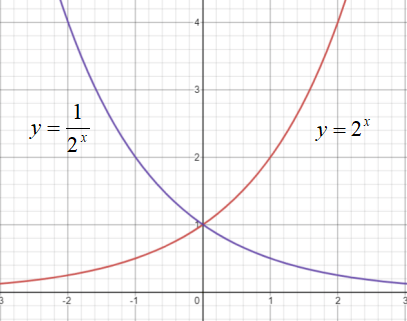
グラフを書くときは、点(0,1)を必ず通りましょう。
x軸を超えることはない
\(a>0,a≠1\)において、指数関数\(y=a^{x}\)のグラフがx軸を超えることはありません。
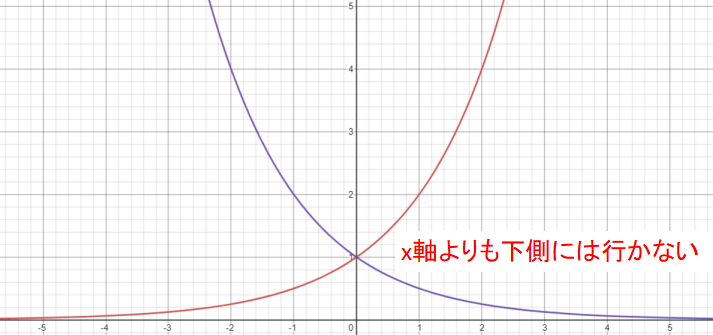
x軸に近づいていく際は、x軸は超えないように注意してください。
以上が指数関数のグラフを書く際の注意ポイントです。
[st-mybox title=”注意ポイント” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点(0,1)を必ず通ること
- x軸を超えることはない
[/st-mybox]
 高校生
高校生これで指数関数のグラフが書けそうです!
“指数関数的に増える”とは?

ニュースで“指数関数的に増える”という言葉を聞いたことはありますか?
「感染者が指数関数的に増える」なんて使い方をすることが多いです。
 高校生
高校生聞いたことあるような、ないような
「指数関数的に」というのは、「指数関数のグラフのように」を意味しています。
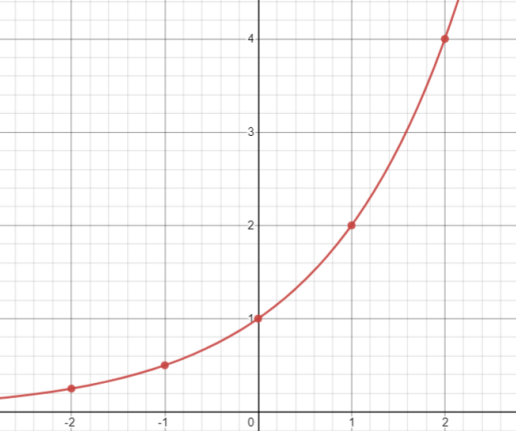
つまり、ものすごい勢いで増加しているということですね。
初めて聞いた方もこれを機会にぜひ覚えておきましょう。
 高校生
高校生グングン増えていることを表しているんだね!
指数と対数の関係
指数とあわせて理解したいのが”対数”です。
[st-mybox title=”指数と対数” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)で\(M>0\)とするとき、次が成り立つ。
\[M=a^{p} \Leftrightarrow log_{a}M=p\]
[/st-mybox]
指数関数\(y=a^{x}\)において、どんな正の数\(M\)に対しても、\(M=a^{p}\)となる実数\(p\)がただ一つ存在する。
この\(p\)を表すのが、対数の\(log_{a}M\)なのです。
\(a\)を底といい、\(M\)をこの対数の真数といいます。
[st-mybox title=”対数の例” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(log_{2}8=p\)のとき、
これは底が2、真数が8の対数なので、式の形を変えて\(2^{p}=8\)と表すこともできます。
よって、\(p=3\)だと分かりますね。
\[log_{2}8=3\]
[/st-mybox]
対数は仕組みを理解すれば難しくありません。
対数関数や対数の計算については別記事で解説しているので、こちらもご覧ください。
指数関数のグラフ《練習問題》
指数関数のグラフについて確認したので、簡単な練習問題に挑戦してみましょう。
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の指数関数のグラフを書きましょう。
(1) \(y=3^{x}\)
(2) \(\displaystyle y=\left(\frac{1}{3}\right)^{x}\)
[/st-mybox]
 高校生
高校生式からグラフがイメージできるようになったよ
練習問題(1)の解説
指数関数\(y=3^{x}\)の通過する点に目印を付けて、滑らかにつないだらグラフの完成です。
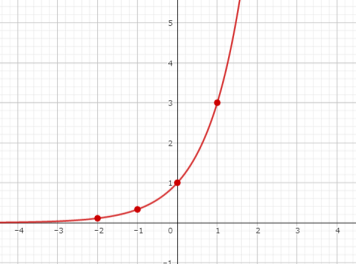
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/9 | 1/3 | 1 | 3 | 9 |
練習問題(2)の解説
指数関数\(\displaystyle y=\left(\frac{1}{3}\right)^{x}\)は底が1より小さいので、右肩下がりのグラフになりそうですね。
通過点に目印を付けて、滑らかに結ぶとグラフが完成します。
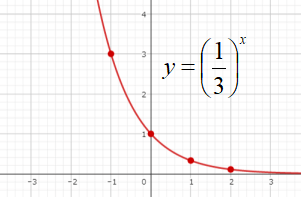
| x | -2 | -1 | 0 | 1 | 2 |
| y | 9 | 3 | 1 | 1/3 | 1/9 |
 高校生
高校生どっちも解けました!
 シータ
シータ指数関数のグラフはバッチリだね!
指数関数 まとめ
今回は指数関数についてグラフを使ってまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 0 0″ myclass=””]指数関数 まとめ[/st-marumozi]
[st-mybox title=”指数関数とは” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a>0,a≠1\)のとき
\[y=a^{x}\]
[/st-mybox]
指数関数のグラフ
[1] \(a>1\)のとき

[st-mybox title=”a>1のとき” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど増加
- \(x\)が小さくなるほど0に近づく
[/st-mybox]
[2] \(a<1\)のとき

[st-mybox title=”a<1のとき” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど0に近づく
- \(x\)が小さくなるほど増加
[/st-mybox]
指数関数のグラフの書き方
[st-mybox title=”指数関数のグラフの書き方” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 分かりやすい通過点に目印を付ける
- a>1ならば右肩上がり、a<1ならば右肩下がりで点をつなぐ
[/st-mybox]
今回は指数関数について解説しました。
指数関数とあわせて押さえておきたいのが対数関数です。
対数関数について詳しくは「対数関数のグラフと書き方3ステップを解説!」で解説しています。
指数関数・対数関数の総復習がしたい方はこちらの記事がおすすめです。
[st-card myclass=”” id=”6455″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[st-mybutton class=”” url=”https://math-travel.jp/shisuu-log/” title=”指数関数・対数関数のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]

