「指数関数の不等式が苦手」
「指数不等式の解き方が分からない」
今回は指数不等式に関するこんな悩みを解決していきます。
高校生指数関数の不等式がどうしても苦手です…
以下のような指数に変数\(x\)を含むような不等式を指数不等式といいます。
\begin{eqnarray}
2^{x}&≧&8\\
\displaystyle \left(\frac{1}{3}\right)^{x+1}&<&\left(\frac{1}{9}\right)^{x}
\end{eqnarray}
指数不等式に似たもので、指数方程式がありますね。
先に指数方程式の解き方を確認しておくと、指数不等式の解き方もスムーズに理解できると思います。
本記事では指数不等式の解き方や注意点を解説します。
例題を用意して解説しているので、ぜひ挑戦してみてください。
記事の内容
※本ページは学習アプリのプロモーションが含まれています。
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
指数関数とは？
まずは指数関数の確認をしておきましょう。
指数関数とは以下のような関数です。
指数関数
\(a>0,a≠1\)のとき
\[y=a^{x}\]
指数関数のグラフは以下のようになります。
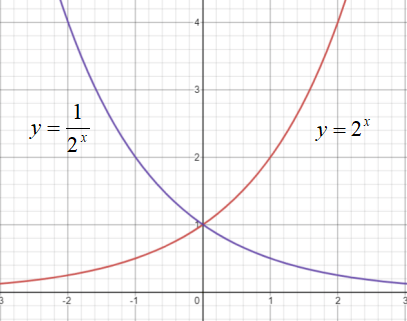
\(a>1\)のときは、赤線の右肩上がりのグラフになります。
一方、\(0<a<1\)のときは右肩下がりの青色のグラフになります。
参考
指数関数のグラフがイメージできない方はこの記事がおすすめ
シータ指数関数についてもしっかり理解しておこう
指数不等式
指数に変数\(x\)を含む不等式を指数不等式といいます。
\begin{eqnarray}
2^{x}&≧&8\\
\displaystyle \left(\frac{1}{3}\right)^{x+1}&<&\left(\frac{1}{9}\right)^{x}
\end{eqnarray}
この不等式を満たす\(x\)の変域を求めるのが、指数不等式の問題です。
指数不等式は指数方程式とほとんど同じ考え方で解きます。
指数方程式が不安な方は先にこちらの記事をご覧ください。
シータ指数方程式が理解できているとスムーズだよ
指数不等式を解くときの注意点
指数不等式を解くときには底\(a\)の値に注意しましょう。
注意ポイント
\(a>0,a≠1\)において
\(a>1\)のとき、\(y=a^{x}\)は増加関数なので
\[a^{m}<a^{n} \Leftrightarrow m<n\]
\(0<a<1\)のとき、\(y=a^{x}\)は減少関数なので
\[a^{m}<a^{n} \Leftrightarrow m>n\]
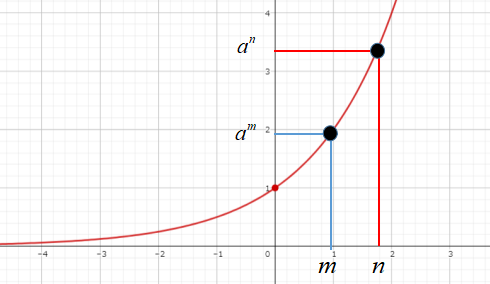
\(a>1\)のときは、グラフが右肩上がりなので\(a^{m}<a^{n}\)のとき、\(m<n\)が成り立ちます。
\(a>1\)のとき、
\[a^{m}<a^{n} \Leftrightarrow m<n\]
しかし、\(a<1\)のときはグラフの右肩下がりになるので不等号の向きが逆になります。
\(0<a<1\)のとき、
\[a^{m}<a^{n} \Leftrightarrow m>n\]
不等式を解いたら、\(a\)の値と不等号の向きをチェックしましょう。
高校生なんだか自信がありません…
シータ実際の問題で解説していくよ
指数不等式の解き方
指数不等式の解き方を4つのパターンに分けて解説します。
指数不等式のパターン
- 底が1より大きいとき
- 底が1より小さいとき
- 置き換える問題
- 対数をとる問題
シータ指数不等式の解き方を解説していくよ！
底が1より大きいとき
底が1より大きい指数不等式はシンプルです。
問題①
次の不等式を解いてみよう。
(1) \(3^{x}<3^{4}\)
(2) \(2^{x}≧8\)
不等式を解く際は、両辺の底をそろえることを目標に式変形をします。
(1)の場合はすでに底が3でそろっていますね。
\[3^{x}<3^{4}\]
底が1より大きいので、指数をそのまま比較できます。
\[x<4\]
これで不等式を解くことができました。
(2)は底をそろえる作業が必要です。
\begin{eqnarray}
2^{x}&≧&8\\
2^{x}&≧&2^{3}
\end{eqnarray}
これで両辺を底2で表すことができました。
底が1より大きいので、不等号の向きは変えずに指数を比較して、
\[x≧3\]
このように底が1より大きい場合は、不等号の向きを変えずに指数を比較します。
高校生これならできる気がするよ！
底が１より小さいとき
底が1より小さいときは不等号の向きに注意しましょう。
問題②
次の不等式を解いてみよう。
(1) \(\displaystyle \left(\frac{1}{2}\right)^{x}<\left(\frac{1}{2}\right)^{3}\)
(2) \(\displaystyle \left(\frac{1}{2}\right)^{x}≧\left(\frac{1}{8}\right)\)
(1)は両辺の底が\(\displaystyle \frac{1}{2}\)で揃っています。
\(\displaystyle \frac{1}{2}<1\)で底が1より小さいので、
\begin{eqnarray}
\displaystyle \left(\frac{1}{2}\right)^{x}&<&\left(\frac{1}{2}\right)^{3}\\
x&>&3
\end{eqnarray}
最後の不等号の向きに気を付けてください。
(2)の不等式も解いてみましょう。
\begin{eqnarray}
\displaystyle \left(\frac{1}{2}\right)^{x}&≧&\left(\frac{1}{8}\right)\\
\displaystyle \left(\frac{1}{2}\right)^{x}&≧&\left(\frac{1}{2}\right)^{3}\\
x&≦&3
\end{eqnarray}
高校生底に気を付けていれば解けそうです
置き換える問題
指数不等式の問題には以下のようなものもあります。
問題③
次の不等式を解いてみよう。
\[2^{2x}-6 \cdot 2^{x} +8<0\]
この問題は\(2^{x}\)を\(t\)に置き換えて、\(t\)の不等式を解きます。
このとき、\(2^{x}>0\)なので\(t>0\)であることに注意しましょう。
\begin{eqnarray}
2^{2x}-6 \cdot 2^{x} +8<0\\
t^{2}-6t+8<0\\
(t-2)(t-4)<0\\
2<t<4
\end{eqnarray}
ここで\(t=2^{x}\)なので、
\begin{eqnarray}
2<2^{x}<4\\
2^{1}<2^{x}<2^{2}\\
1<x<2
\end{eqnarray}
\(t>0\)であることに注意して不等式を解きましょう。
シータ置き換えると解きやすくなるよ！
対数をとる問題
両辺の底をそろえることができない不等式もあります。
問題④
次の不等式を解いてみよう。
(1) \(2^{x}≦5\)
(2) \(3^{x}>12\)
同じ底で表せないときは、両辺の対数をとりましょう。
この問題の場合は、\(log_{2}\)で対数をとると計算しやすくなります。
\begin{eqnarray}
2^{x}&≦&5\\
log_{2}2^{x}&≦&log_{2}5\\
x log_{2}2&≦&log_{2}5\\
x&≦&log_{2}5
\end{eqnarray}
(2)の問題も見てみましょう。
\begin{eqnarray}
3^{x}&>&12\\
log_{3}3^{x}&>&log_{3}12\\
x log_{3}3&>&log_{3}(3 \cdot 4)\\
x&>&log_{3}3+log_{3}2^{2}\\
x&>&1+2 log_{3}2
\end{eqnarray}
シータ別単元でも対数をとることがあるので、慣れておきましょう！
指数不等式《練習問題》
指数不等式の練習問題にチャレンジしてみましょう！
練習問題
次の不等式を解いてみよう。
(1) \(3^{x}≦27\)
(2) \(9^{x}-10 \cdot 3^{x}+9>0\)
(3) \(2^{x+3}>5^{x+1}\)
シータどの解き方で解くのか考えてみよう！
練習問題1の解説
練習問題1
次の不等式を解いてみよう。
(1) \(3^{x}≦27\)
この問題は指数不等式のなかでも1番簡単な問題です。
\begin{eqnarray}
3^{x}&≦&27\\
3^{x}&≦&3^{3}\\
x&≦&3
\end{eqnarray}
底が1より大きいので、不等号の向きはそのままで大丈夫です。
基本的な指数不等式がまだ不安な方は、底をそろえる問題の解き方に戻ってもう一度確認しましょう。
高校生この問題はもう大丈夫そうです
練習問題2の解説
練習問題2
次の不等式を解いてみよう。
(2) \(4^{x}-3 \cdot 2^{x}-4>0\)
これは置き換えの問題ですね。
\(2^{x}=t\)とすると、\(t>0\)であり、不等式は
\begin{eqnarray}
t^{2}-3t-4>0\\
(t+1)(t-4)>0\\
\end{eqnarray}
ここで\(t+1>0\)なので,
\(t-4>0\)すなわち\(t>4\)
よって
\begin{eqnarray}
2^{x}>4\\
2^{x}>2^{2}\\
x>2
\end{eqnarray}
難しそうな問題に見えますが、\(t\)に置き換えることで二次不等式を解くだけの問題です。
置き換える問題の解き方を再確認したい方はこちら
高校生解き方を覚えたのでこれからは解けそうです！
練習問題3の解説
最後は両辺に対数をとる問題ですね。
練習問題3
次の不等式を解いてみよう。
(3) \(2^{x+3}>5^{x+1}\)
今回は\(log_{2}\)で対数をとって計算してみましょう。
\begin{eqnarray}
\log_{2}2^{x+3}&>&log_{2}5^{x+1}\\
(x+3)log_{2}2&>&(x+1)log_{2}5\\
(x+3)&>&(x+1)log_{2}5\\
(1-log_{2}5)x&>&log_{2}5-3
\end{eqnarray}
ここで\(1-log_{2}5<0\)なので不等号の向きに注意して、
\begin{eqnarray}
\displaystyle x&<&\frac{log_{2}5-3}{1-log_{2}5}\\
\displaystyle x&<&\frac{3-log_{2}5}{log_{2}5-1}\\
\end{eqnarray}
これで対数をとる不等式を求めることもできましたね。
対数をとるパターンが苦手な方は、ひとまずたくさん問題を解いてみて少しずつ慣れていくのが良いと思います。
シータ対数のことを忘れがちなので注意
指数不等式 まとめ
今回は指数不等式についてまとめました。
指数不等式 まとめ指数不等式の問題にはパターンがある。
指数不等式のパターン
- 底が1より大きいとき
- 底が1より小さいとき
- 置き換える問題
- 対数をとる問題
指数不等式を解くとき、底\(a\)の値に注意する。
注意ポイント
\(a>0,a≠1\)において
1.\(a>1\)のとき、\(y=a^{x}\)は増加関数なので
\[a^{m}<a^{n} \Leftrightarrow m<n\]
2.\(0<a<1\)のとき、\(y=a^{x}\)は減少関数なので
\[a^{m}<a^{n} \Leftrightarrow m>n\]
指数の方程式や不等式を求める計算過程で、指数法則と対数法則をよく使います。
指数法則と対数法則については別記事で解説しているので、こちらも合わせてご覧ください。
指数関数・対数関数の総復習がしたい方にはこちらの記事がおすすめです。
コメント