数学Bの数列で出てくる「∑(シグマ)」に悩まされる高校生も多いはず。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”50px auto 40px”]
「シグマの公式が分からない」
「数列のシグマの計算が苦手」
[/st-mybox]
今回は数列のシグマに関する悩みを解決します。
 高校生
高校生Σシグマの公式を忘れてしまって、数列の和が求められない…
数列の和を求める問題など、さまざまな所でΣ(シグマ)を使います。
まず前提の知識として、Σ(シグマ)とは総和を表す記号で、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+ \cdots +a_{n}\]
[/st-mybox]
を表しています。
例えば、\(\displaystyle \sum_{k=3}^{10} a_{k}\)のときは、\(a_{n}\)のn=3からn=10までの足し算を意味します。
\[\displaystyle \sum_{k=3}^{10} a_{k}=a_{3}+a_{4}+ \cdots +a_{10}\]
そんなシグマには絶対に覚えておきたい5つの公式があります。
[st-mybox title=”Σの計算公式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
本記事ではΣシグマの計算公式と性質について解説します。
Σの計算ができないのは公式を覚えていない場合が多いです。本記事を読んで、ぜひ覚えてしまいましょう。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
Σシグマの計算公式
Σシグマを学習するにあたって、確実に覚えておきたい公式が5つあります。
[st-mybox title=”Σの計算公式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
どれも重要な公式なので、必ず覚えましょう。
シグマの計算公式の証明は「4. Σシグマの公式の証明」で解説します。
 シータ
シータこれからは当たり前のように公式を使うからね
Σシグマの性質
Σシグマの計算公式と合わせて、以下の性質も覚えておきましょう。
[st-mybox title=”Σシグマの性質” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(p,q\)は定数とすると、
\(\displaystyle 1.\sum_{k=1}^{n}(a_{k}+b_{k})=\sum_{k=1}^{n} a_{k}+\sum_{k=1}^{n} b_{k}\)
\(\displaystyle 2.\sum_{k=1}^{n} pa_{k}=p\sum_{k=1}^{n} a_{k}\)
1,2より
\(\displaystyle \sum_{k=1}^{n}(pa_{k}+qb_{k})=p\sum_{k=1}^{n} a_{k}+q\sum_{k=1}^{n} b_{k}\)
[/st-mybox]
それぞれの性質について証明します。
[st-mybox title=”Σシグマの性質①の証明” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
[st-mybox title=”Σシグマの性質②の証明” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
数列\(\{a_{n}\}\)に対して、\(p\)を定数とすると
\(\displaystyle \sum_{k=1}^{n} pa_{k}\)
\(\displaystyle =pa_{1}+pa_{2}+\cdots+pa_{n}\)
\(\displaystyle =p(a_{1}+a_{2}+\cdots+a_{n})\)
\(\displaystyle =p\sum_{k=1}^{n} a_{k}\)
[/st-mybox]
[st-mybox title=”Σシグマの性質③の証明” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
以上のΣの計算公式と性質を利用すれば、様々な数列の和も求めることができます。
 高校生
高校生かっこの中身を分けたりできるんだね!
 シータ
シータそういうこと!工夫して計算するのが大事だよ!
Σシグマを利用する問題
Σシグマの基本問題
実際に公式や性質を使って、いくつか問題を解いてみましょう。
まずは超基本となる計算問題から
[st-mybox title=”Σシグマの基本問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の計算をしてみよう。
\(\displaystyle 1.\sum_{k=1}^{n} 3k\)
\(\displaystyle 2.\sum_{k=1}^{n} (k^{2}+2k)\)
\(\displaystyle 3.\sum_{k=1}^{n} 3 \cdot 2^{k}\)
[/st-mybox]
(1)の解説
(1)の問題は定数の3を前に出すことで、Σの計算公式②の等差数列の和が使えます。
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} 3k&=&3 \sum_{k=1}^{n} k\\
\displaystyle &=&3 \cdot \frac{1}{2}n(n+1)\\
\displaystyle &=&\frac{3}{2}n(n+1)
\end{eqnarray}
[st-mybox title=”使った公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \sum_{k=1}^{n} k=\frac{1}{2}n(n+1)\]
[/st-mybox]
(2)の解説
[st-mybox title=”使った公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \sum_{k=1}^{n} k=\frac{1}{2}n(n+1)\]
\[\displaystyle \sum_{k=1}^{n} k^{2}=\frac{1}{6}n(n+1)(2n+1)\]
[/st-mybox]
(3)の解説
(3)の問題は計算公式⑤で紹介した等比数列の和として考えます。
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} 3 \cdot 2^{k}&=&3 \sum_{k=1}^{n} 2^{k}\\
\displaystyle &=&3 \cdot \frac{2(2^{n}-1)}{2-1}\\
\displaystyle &=&6(2^{n}-1)
\end{eqnarray}
等差数列や等比数列の和の公式をまだ覚えてない人はすぐに確認しましょう!
[st-mybox title=”要チェック!” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
 シータ
シータこれは公式を覚えてスラスラと解けて欲しいな
 高校生
高校生公式を覚えたから計算ならできそう!
一般項を求めてから和を求める問題
以下のような一般項を求めてから和を求める問題もあります。
[st-mybox title=”数列の和” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の数列の初項から第\(n\)項までの和を求めよう。
\[1 , 6 , 11 , 16 , 21 , …\]
[/st-mybox]
この問題はまず数列の一般項\(a_{n}\)を求める必要があります。
なぜなら、一般項で表すことでΣの計算ができるようになるからです。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
1 , 6 , 11 , 16 , 21 , …
[/st-mybox]
与えられた数列は「初項1、公差5の等差数列」です。
したがって、一般項\(a_{n}\)は
\begin{eqnarray}
a_{n}&=&1+5(n-1)\\
&=&5n-4
\end{eqnarray}
一般項が分かればあとはΣの計算をするだけです。
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} a_{k}&=&\sum_{k=1}^{n} (5k-4)\\
\displaystyle &=&5 \sum_{k=1}^{n} k – \sum_{k=1}^{n} 4\\
\displaystyle &=&5 \cdot \frac{1}{2}n(n+1) – 4n\\
\displaystyle &=&\frac{1}{2}n(5n-3)
\end{eqnarray}
したがって、与えられた数列の初項から第\(n\)項までの和を求めることができました。
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
等差数列の一般項の求め方は「等差数列の一般項と和の公式を分かりやすく解説!」で解説しています。
[/st-mybox]
[st-card myclass=”” id=”6221″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
数列の一般項を求める
数列の一般項を求めるときにもΣを使います。

数列\(\{a_{n}\}\)の隣り合う項の差でできた数列\(\{b_{n}\}\)を階差数列といいます。
もとの数列の一般項\(a_{n}\)を求めるには、初項\(a_{1}\)に対して階差数列\(\{b_{n}\}\)を加えるイメージで考えます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a_{1}=a_{1}\) ←初項
\(a_{2}=a_{1}+b_{1}\)
\(\displaystyle a_{3}=a_{2}+b_{2}=a_{1}+\sum_{k=1}^{2} b_{k}\)
\(\displaystyle a_{4}=a_{3}+b_{3}=a_{1}+\sum_{k=1}^{3} b_{k}\)
:
\(\displaystyle a_{n}=a_{n-1}+b_{n-1}=a_{1}+\sum_{k=1}^{n-1} b_{k}\)
[/st-mybox]
したがって、元の数列の一般項\(a_{n}\)は
\[\displaystyle a_{n}=a_{n-1}+b_{n-1}=a_{1}+\sum_{k=1}^{n-1} b_{k}\]
で求めることができます。
階差数列については「階差数列を用いた一般項と和を求める公式!」で詳しくまとめました。
分数の和は部分分数分解
以下のような分数の和はシグマではなく部分分数分解で解きます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
 高校生
高校生部分分数分解…漢字が多くて難しそう…
なんだか難しそうと思った方も多いですよね。
部分分数分解とは、以下のように1つの分数を分解することを指します。
[st-mybox title=”部分分数分解” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}\]
[/st-mybox]
部分分数分解を利用すると、与えられた分数の和も
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
それぞれの分数が符号の違うもの同士で相殺するので、シンプルな答えになります。
 高校生
高校生これは部分分数分解を知らないと困っちゃうね
 シータ
シータそうなんだよ。分数の和をみたら部分分数分解を疑ってみよう
4. Σシグマの公式の証明
「1.Σシグマの計算公式」で紹介したΣシグマの公式を証明します。
証明を読まない方は飛ばしてもらって大丈夫なところです。
[st-mybox title=”Σシグマの計算公式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
[st-mybox title=”公式の証明①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a\)が\(k\)を含んでいないので\(\displaystyle \sum_{k=1}^{n} a\)というのは、\(a\)を\(n\)回足すことを意味します。
したがって、
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} a&=&a+a+ \cdot + a\\
&=&an
\end{eqnarray}
[/st-mybox]
[st-mybox title=”公式の証明②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \sum_{k=1}^{n} k=1+2+3+\cdots +n\]
これは「初項1、末項\(n\)、項数\(n\)の等差数列の和」を表しています。
右辺を等差数列の和の公式に置き換えて
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} k&=&1+3+ \cdot + n\\
\displaystyle &=&\frac{1}{2}n(n+1)
\end{eqnarray}
[/st-mybox]
[st-mybox title=”公式の証明③” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
恒等式
\[(k+1)^{3}-k^{3}=3k^{3}+3k+1\]
を利用します。
\(k=1,2,3,\cdots,n\)とすると
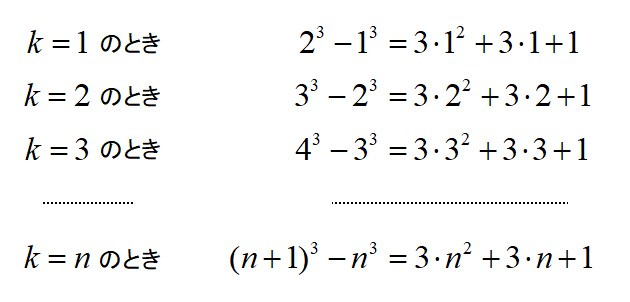
これらの式の両辺を加えると、
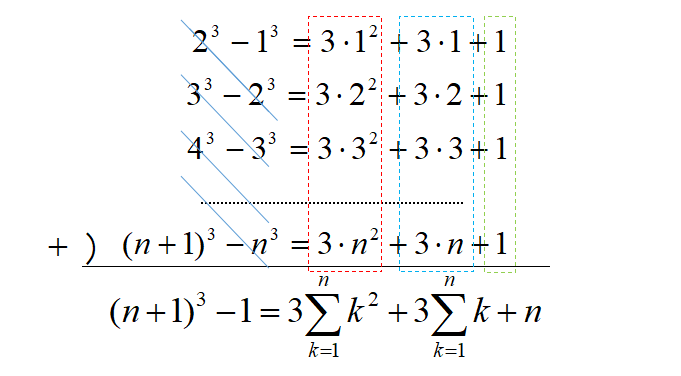
これらを移項して、
\[\displaystyle 3\sum_{k=1}^{n} k^{2}=(n+1)^{3}-1-3\sum_{k=1}^{n} k -n\]
ここで\(\displaystyle \sum_{k=1}^{n} k =\frac{1}{2}n(n+1)\)を代入して
最後に両辺を3で割って、
\[\displaystyle \sum_{k=1}^{n} k^{2}=\frac{1}{6}n(n+1)(2n+1)\]
[/st-mybox]
[st-mybox title=”公式の証明④” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
恒等式
\[(k+1)^{4}-k^{4}=4k^{3}+6k^{2}+4k+1\]
を利用します。
\(k=1,2,3,\cdots,n\)とすると
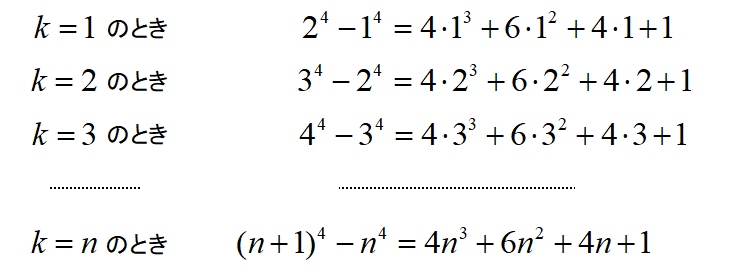
これらの式の両辺を加えると、
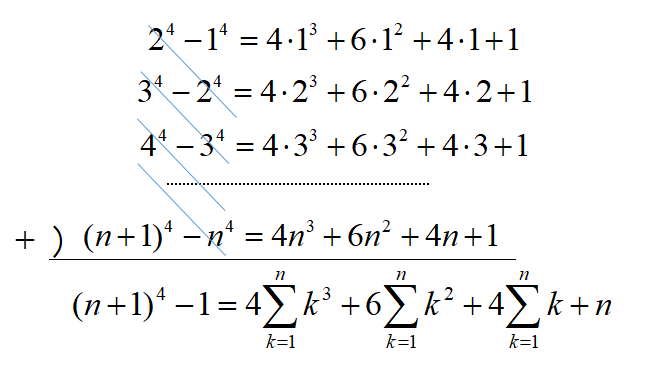
これらを移項して、
ここで
\(\displaystyle \sum_{k=1}^{n} k =\frac{1}{2}n(n+1)\)
\(\displaystyle \sum_{k=1}^{n} k^{2}=\frac{1}{6}n(n+1)(2n+1)\)
を代入して、式を整理すると、
\[\displaystyle 4\sum_{k=1}^{n} k^{3}=n^{2}(n+1)^{2}\]
最後に両辺を4で割って、
\[\displaystyle \sum_{k=1}^{n} k^{3}=\{\frac{1}{2}n(n+1)\}^{2}\]
[/st-mybox]
[st-mybox title=”公式の証明⑤” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\displaystyle \sum_{k=1}^{n} ar^{k-1}=a+ar+\cdots +ar^{n-1}\]
これは「初項\(a\)、公比\(r\)、項数\(n-1\)の等比数列の和」を表しています。
右辺を等比数列の和の公式に置き換えると
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} ar^{k-1}&=&a+ar+\cdots +ar^{n-1}\\
\displaystyle &=&\frac{a(r^{n}-1)}{r-1} (r > 0)\\
\displaystyle &=&\frac{a(1-r^{n})}{1-r} (r < 0)
\end{eqnarray}
[/st-mybox]
公式の証明はできなくても問題ないので、まずは5つの公式を確実に使えるようになりましょう。
《重要》3つの基本数列
今回はΣシグマの公式や性質について解説しました。
シグマは数列の和を求めるときに活躍しますが、そもそも数列の一般項を求められないとシグマを活用できません。
以下の数列はかなり重要なので確実に押さえておきましょう。
[st-mybox title=”基本の数列” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 等差数列
- 等比数列
- 階差数列
[/st-mybox]
・等差数列
等差数列とは、「一定の差で変化する数列」を指します。

・等比数列
等比数列とは、「初めの項に一定の数をかけ続けていく数列」を指します。
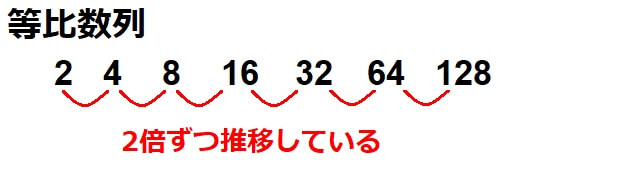
・階差数列
階差数列は複雑で、各項の差を書き出してみるとある数列が見えてきます。
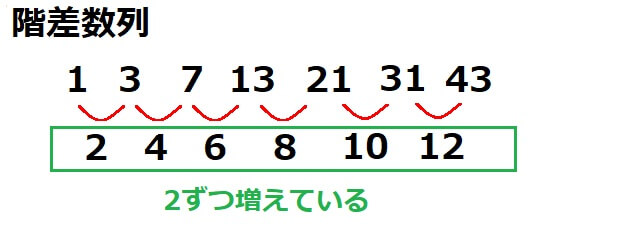
上の数列の場合、各項の差が等差数列になっています。
この差が等比数列になる場合もありますし、もっと複雑な数列になるときもあります。
数Bの数列についてまとめ記事を作りました。
基礎から確認したい方はぜひご覧ください。
[st-card myclass=”” id=”6197″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
Σシグマの公式 まとめ
今回はΣシグマの計算公式や性質についてまとめました。
[st-minihukidashi fontawesome=”fa-file-text-o” fontsize=”90″ fontweight=”” bgcolor=”#FFC107″ color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]Σシグマの公式 まとめ[/st-minihukidashi]
[st-mybox title=”Σの計算公式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
[st-mybox title=”Σシグマの性質” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(p,q\)は定数とすると、
\(\displaystyle 1.\sum_{k=1}^{n}(a_{k}+b_{k})=\sum_{k=1}^{n} a_{k}+\sum_{k=1}^{n} b_{k}\)
\(\displaystyle 2.\sum_{k=1}^{n} pa_{k}=p\sum_{k=1}^{n} a_{k}\)
1,2より
\(\displaystyle \sum_{k=1}^{n}(pa_{k}+qb_{k})=p\sum_{k=1}^{n} a_{k}+q\sum_{k=1}^{n} b_{k}\)
[/st-mybox]
数列の単元は覚えることは多いですが、問題のパターンが限られています。
それぞれの性質や公式をしっかりと覚えれば、数列はベクトルよりも得点しやすい単元です。
 高校生
高校生Σの計算が苦手だと思っていたけど、公式を覚えていないだけだったんだね!
 シータ
シータそうそう!公式を覚えていれば特に難しいことはしていないよ
Σの計算がスムーズにできると、数列の和や群数列の問題でも素早く解くことができます。
各数列の性質や、漸化式、群数列について知りたい方は「数列まとめ記事」をご覧ください。
[st-card myclass=”” id=”6197″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[st-mybutton class=”” url=”https://math-travel.jp/suuretu/” title=”数列のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]

