数学Ⅰ三角比のなかで多くの高校生を苦しめるのが「正弦定理」です。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 40px”]
「正弦定理の公式を忘れてしまった」
「正弦定理の使い方が分からない」
[/st-mybox]
今回は正弦定理に関するこんな悩みを解決します。
 高校生
高校生正弦定理がよく分からなくて…
今回は三角比の正弦定理について解説していきます。
[st-mybox title=”正弦定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCの外接円の半径をRとすると、次が成り立つ。
\[\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
[/st-mybox]
さっそくですが下の三角形ABCをみて、辺ABの長さが分かりますか?
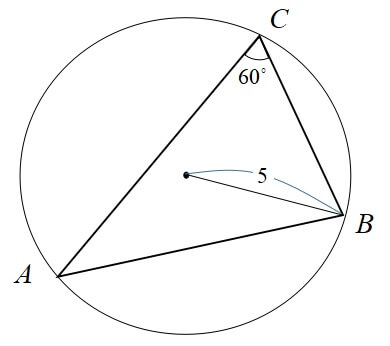
「これだけじゃ分からないよ!」
こう思った方は正弦定理を使いこなせていないので要注意です!
実は”正弦定理”を使うことで三角形の辺の長さや角の大きさを簡単に求めることができるのです!
今回は正弦定理の公式や使い方について記事を書いたのでぜひ最後までご覧ください。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
正弦定理の公式

正弦定理は三角比の重要な公式の1つです。
各頂点A,B,Cとして、向かい合う辺をa,b,cとしましょう。
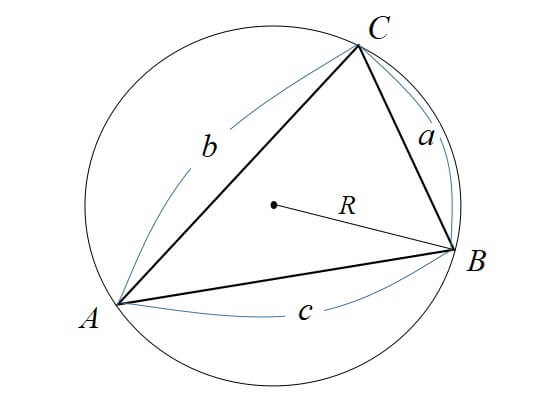
[st-mybox title=”正弦定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCの外接円の半径をRとすると、次が成り立つ。
\[\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
[/st-mybox]
正弦定理を活用することで、辺や角の大きさを求めることができます。
 高校生
高校生公式は覚えてるけど使い方がよく分からなくて…
 シータ
シータ例題をもとに正弦定理を使ってみよう!
正弦定理の使い方
以下の問題を例にして正弦定理の使い方を解説します。
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
半径5cmの円に内接する三角形ABCがあります。
\(C=60^\circ\)のとき、辺ABの値を求めよう。

[/st-mybox]
上の問題では円の半径と角の大きさが分かっているので、正弦定理を用いて考えます。
辺ABの大きさをcとすると正弦定理より、
\begin{eqnarray}
\displaystyle \frac{c}{\sin C}&=&2R\\
\displaystyle \frac{c}{\sin 60^\circ}&=&2 \times 5\\
c&=&10 \sin 60^\circ\\
c&=&5\sqrt{3}
\end{eqnarray}
したがって、ABの大きさは\(5\sqrt{3}\)だと分かりました。
正弦定理の証明
なぜ正弦定理が成り立つのか証明していきましょう。
証明の方針としては、角Aの大きさを場合分けして考えます。
\([1] 0^\circ < A < 90^\circ\)のとき
三角形の3つの頂点を通す円を、その三角形の外接円といいます。
△ABCの外接円の半径をRとしましょう。
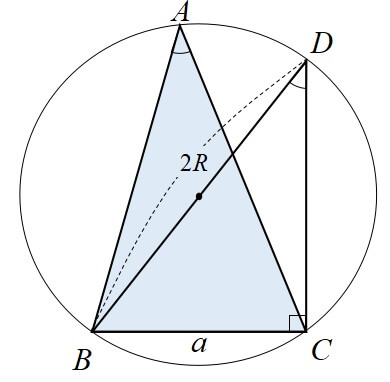
点Aとは異なる点Dを円周上にとり、直角三角形\(DCB\)を作ります。
円周角と中心角の性質により、
\[\angle BDC = \angle BAC \]
また、\(\angle BCD = 90^\circ\)より、
\[BD=2R\]
△BCDにおいて
\begin{eqnarray}
a&=&2R\sin \angle BDC\\
&=&2R\sin \angle BAC
\end{eqnarray}
が成り立つ。
したがって、
\[\displaystyle \frac{a}{\sin A}=2R\]
\([2] A = 90^\circ\)のとき
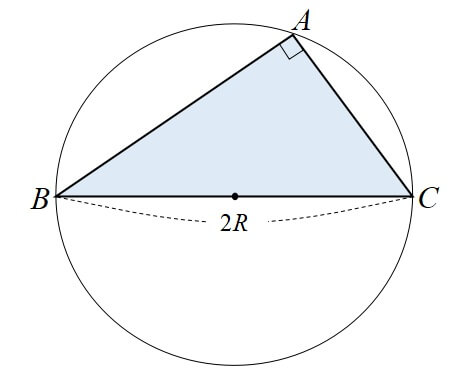
辺BCは、△ABCの外接円の直径になので
\[a=2R\]
一方で、\(\sin A=\sin 90^\circ=1\)なので、
\[a=2R\sin A\]
したがって、
\[\displaystyle \frac{a}{\sin A}=2R\]
\([3] 90^\circ < A < 180^\circ\)のとき
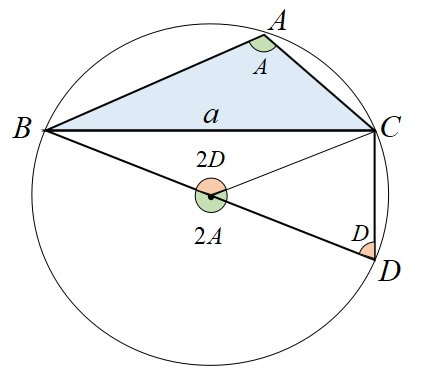
上の図で、線分BDは△ABCの外接円の直径とする。
\(\angle BDC=D\)とすると、円周角と中心角の性質より
\[2A+2D=360^\circ\]
すなわち、
\[A+D=180^\circ\]
\begin{eqnarray}
\sin D&=&\sin(180^\circ -A)\\
&=&\sin A
\end{eqnarray}
ここで、
\(\angle BCD=90^\circ、BD=2R\)であるから、△BCDにおいて、
\begin{eqnarray}
a&=&2R\sin D\\
&=&2R \sin (180^\circ -A)\\
&=&2R \sin A
\end{eqnarray}
したがって、
\[\displaystyle \frac{a}{\sin A}=2R\]
[1]~[3]より、正弦定理の証明終了。
余弦定理との使い分け
正弦定理とあわせて覚えておきたいのが余弦定理です。
三角形ABCの向かい合う辺をa,b,cとすると、
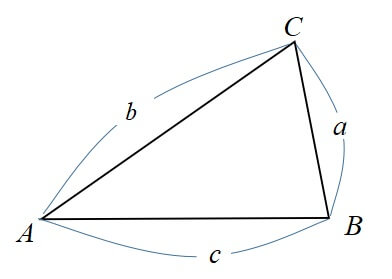
[st-mybox title=”余弦定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCにおいて、次が成り立つ。
\begin{eqnarray}
a^{2}=b^{2}+c^{2}-2bc \cos A\\
b^{2}=a^{2}+c^{2}-2ac \cos B\\
c^{2}=a^{2}+b^{2}-2ab \cos C
\end{eqnarray}
[/st-mybox]
名前の似ている2つの定理ですが、使い分けに困ることがあるはずです。
それぞれの定理を使うタイミングをざっくりとまとめました。あくまで参考程度にご覧ください。
[st-mybox title=”正弦定理と余弦定理” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
正弦定理を使う時
①1辺と2つの角が与えられている場合
②1組の向かい合う辺と角が与えられている場合
③外接円の半径を求めたい場合
余弦定理を使う時
①2辺とその間の角が与えられている場合
②3辺が与えられているとき
[/st-mybox]
「5つも覚えられないよ!」
そんな方は以下のように覚えましょう。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
辺よりも角の情報が多い ⇒ 正弦定理
角よりも辺の情報が多い ⇒ 余弦定理
[/st-mybox]
 高校生
高校生これなら覚えやすいです!!
 シータ
シータ必ず使えるわけではないので、参考程度に使ってね
正弦定理の公式《練習問題》
今回学んだ正弦定理を用いて、練習問題に挑戦してみましょう。
[st-mybox title=”練習問題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a=5,A=45^\circ\)の三角形ABCにおいて、外接円の半径\(R\)を求めよう。
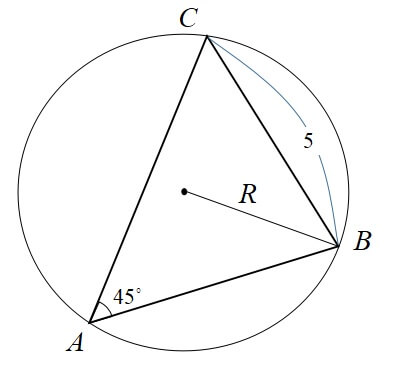
[/st-mybox]
解説
正弦定理より、
\begin{eqnarray}
\displaystyle 2R&=&\frac{a}{sin A}\\
\displaystyle &=&\frac{5}{sin 45^\circ}\\
\displaystyle &=&\frac{5}{\frac{1}{\sqrt{2}}}\\
&=&5\sqrt{2}
\end{eqnarray}
したがって、
\[\displaystyle R=\frac{5\sqrt{2}}{2}\]
[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(△ABC\)において\(c=10\)で、外接円の半径が\(R=10\)のとき、\(\angle C\)の大きさを求めよう。
[/st-mybox]
解説
正弦定理
\begin{eqnarray}
\displaystyle \frac{c}{sin C}&=&2R\\
\displaystyle \frac{10}{sin C}&=&20\\
\displaystyle sin C=\frac{1}{2}
\end{eqnarray}
したがって、
\[\angle C=30^\circ,150^\circ\]
 高校生
高校生正弦定理が使えるようになりました!
正弦定理の公式 まとめ
今回は正弦定理の公式についてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]正弦定理 まとめ[/st-marumozi]

[st-mybox title=”正弦定理” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCの外接円の半径をRとすると、次が成り立つ。
\[\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
[/st-mybox]
正弦定理を使うことで、辺の長さや角の大きさを求めることができます。
[st-mybox title=”正弦定理と余弦定理” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
正弦定理を使う時
①1辺と2つの角が与えられている場合
②1組の向かい合う辺と角が与えられている場合
③外接円の半径を求めたい場合
余弦定理を使う時
①2辺とその間の角が与えられている場合
②3辺が与えられているとき
[/st-mybox]
そして、正弦定理とあわせて理解したいのが余弦定理です。
[st-card myclass=”” id=”2325″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
三角関数には重要な公式がたくさんあります。
三角関数の重要ポイントをまとめた記事はこちら
[st-card myclass=”” id=”2005″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

