循環小数の例と分数に直す方法

「循環小数ってなに？」
「循環小数を分数に直したい」

今回はこんな悩みを解決していきます。

そもそも循環小数というものを聞いたことありますか？

こういった、同じ数字を繰り返す小数を「循環小数」いいます。

同じ数字を循環するから循環小数と呼びます。

本記事では、循環小数の例と分数に直す方法を解説していきます。

循環小数の例

循環小数の例を見ていく前に、小数には大きく2種類のものがあります。

• 有限小数
• 無限小数

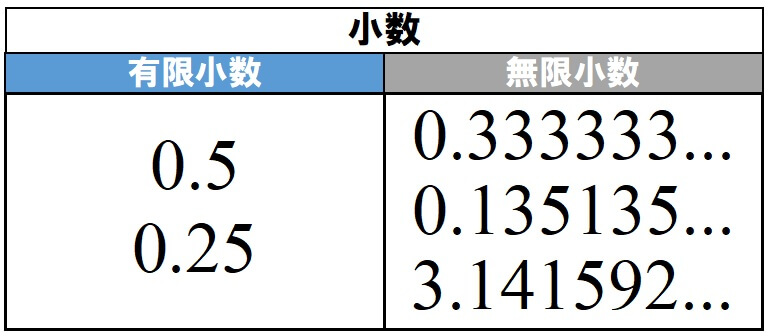
有限小数というのは、0.5,0.25のような、数字が止まる小数のこと。

無限小数というのは、0.3333…,3.141592…のような、無限に続く小数のこと。

そして、無限小数のなかにも２種類の無限小数があります。

同じ数字が繰り返される「循環小数」

規則性がない「循環しない小数」

循環小数の例としては、

0.33333…
0.135135135…

などがあります。

循環小数が何なのかはわかりましたね！

ただし、ここで１つ問題が発生します。

「循環小数はどこまで書けばいいですか？」

良い質問ですね。

循環小数は、繰り返さえれる部分を・で囲み省略して書き表します。

0.33333…のとき

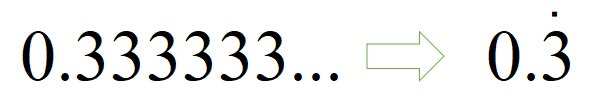
繰り返し始める先頭の数字に・と付けることで、それ以降を省略することができます。

1.424242…のとき

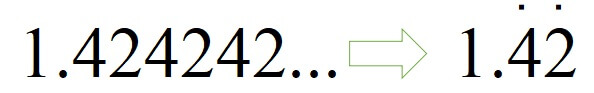
小数部分の42が繰り返されているので、４と２に・を付けることで、繰り返すことを表します。

0.135135135…のとき

このように、循環部分が３桁以上の時も、2桁のときと同様です。
循環部分のはじめと終わりに・を付けることで、その部分が繰り返すことを表します。

これで、循環小数をどこまで書き表すか問題が解決しました。

循環小数を分数に直す方法

循環小数を分数に直す方法を伝授していきます。

例えば、こんな問題が出ます。

問題　循環小数\(0.\dot{3}\)を分数で表せ。

\(0.\dot{3}=0.33333…\)

なので、

勘の鋭い方なら、なんとなく\(\displaystyle \frac{1}{3}\)かなぁって感じると思います。

だけど、それ本当に？といわれたらムムムって感じですよね。

他にも、\(0.\dot{1}3\dot{5}\)は分数で表せるかと聞かれると、感覚で解くのは難しいですね。

実は、循環小数の分数に直す方法はめっちゃ簡単です。

はじめに\(0.\dot{3}\)でやってみます。

求めたい循環小数を\(x\)と置きます。

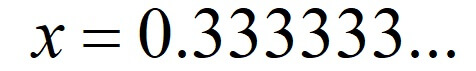
循環小数の何が嫌って、後ろに無限に続く部分が嫌ですよね。

そこを消すことを考えます。

\(x=0.3333…\)を10倍することで、

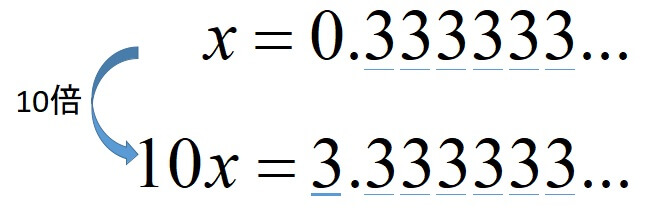
繰り返している部分を、1つ分ずらすことができました。

これで式の減法をすると、

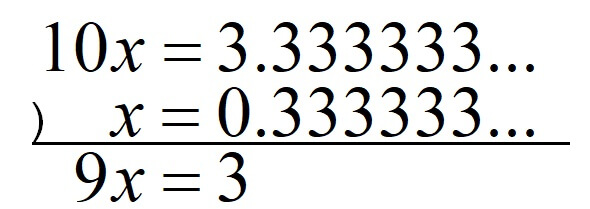
\(9x=3\)

\(x=\displaystyle \frac{3}{9}\)

\(x=\displaystyle \frac{1}{3}\)

となり、

\(x=0.3333…\)なので、

\(0.\dot{3}=\displaystyle \frac{1}{3}\)

次に、\(0.\dot{1}3\dot{5}\)を分数に直していきましょう。

求めたい循環小数を\(x\)と置きます。

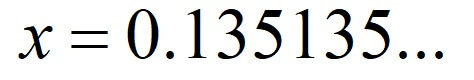
先程と同じように、後ろの繰り返し部分を消したいのです。

しかし、10倍だと繰り返し部分1つ分はズレません。

今回の場合は、\(x=0.135135\)を1000倍することで、

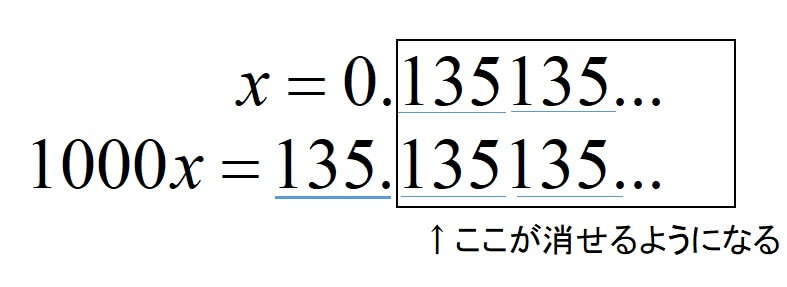
繰り返している部分を、1つ分ずらすことができました。

これで式の減法をすると、

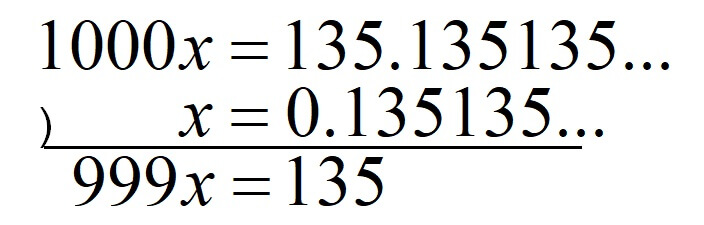
\(999x=135\)

\(x=\displaystyle \frac{135}{999}\)

\(x=\displaystyle \frac{5}{37}\)

となり、

\(x=0.135135…\)なので、

\(0.\dot{1}3\dot{5}=\displaystyle \frac{5}{37}\)

これで、循環小数を分数に直すことができるようになりました。

分数を循環小数で表す

逆に、分数を循環小数で表すこともできます。

例えば、\(\displaystyle \frac{7}{15}\)を循環小数で表します。

\(\displaystyle \frac{7}{15}\)というのは、\(7\div｛{15}\)なので、

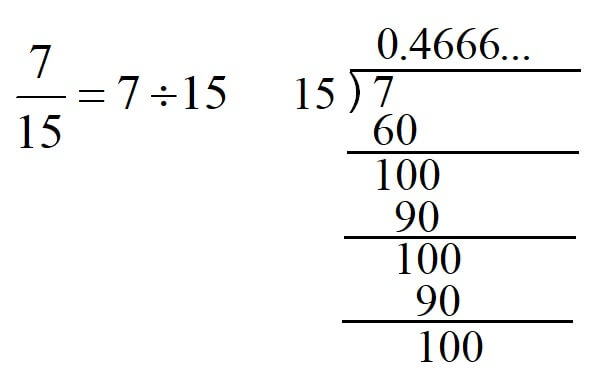
\(\displaystyle \frac{7}{15}=0.4666…\)

したがって、

\(\displaystyle \frac{7}{15}=0.4\dot{6}\)

となり、循環小数の形に表すことができました。

循環小数《練習問題》

では、今日学んだことを使って練習問題を解いていきましょう。

解答

１．\(x=1.\dot{4}\dot{2}\)とする。

今回繰り返し部分を1つ分ずらすとしたら、100倍すればよい。

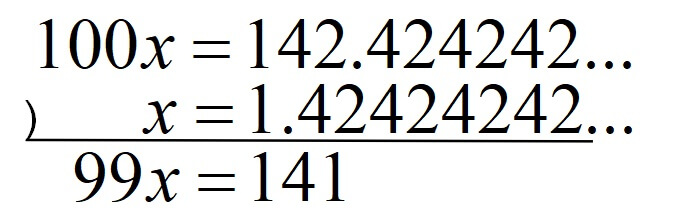
\(99x=141\)

\(x=\displaystyle \frac{141}{99}\)

\(x=\displaystyle \frac{47}{33}\)

となり、

\(x=1.424242…\)なので、

\(1.\dot{4}\dot{2}=\displaystyle \frac{47}{33}\)

２．\(\displaystyle \frac{11}{12}=11\div{12}\)なので、

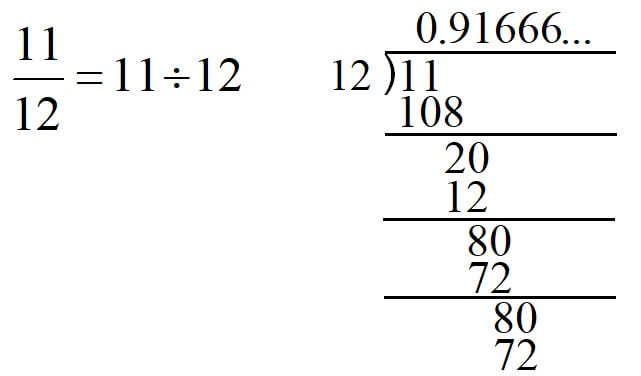
したがって、

\(\displaystyle \frac{11}{12}=0.91\dot{6}\)

循環小数　まとめ

今回は数学Aの循環小数の例と分数の表し方についてサクッとまとめました。

教科書に内容に沿ってどんどん解説記事を挙げていくので、
お気に入り登録しておいてもらえると定期試験前に確認できると思います。

では、ここまで読んでくださってありがとうございました。

みんなの努力が報われますように！