[st-mybox title=”” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
「内分点・外分点の公式が知りたい」
「公式の使い方が知りたい」
[/st-mybox]
図形の単元が苦手な方は必見です!
今回は内分点・外分点に関する悩みを解決します。
 高校生
高校生内分・外分が苦手で…

「内分点」「外分点」は高校数学で何度も登場する重要な点です。
平面座標だけでなく、ベクトルや複素数にも内分点・外分点は登場します。
[st-midasibox title=”座標平面の内分点・外分点” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold” myclass=””]
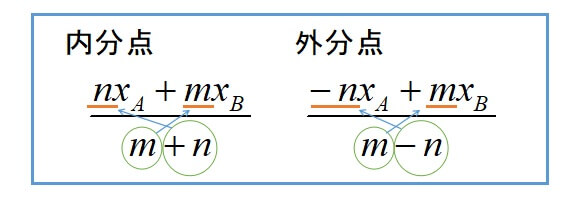
座標平面上の2点\(A(x_{1},y_{1}),B(x_{2},y_{2})\)について、線分ABを\(m:n\)に内分する点をP、\(m:n\)に外分する点をQとすると、
点Pの座標
\[\displaystyle (\frac{nx_{1}+mx_{2}}{m+n},\frac{ny_{1}+my_{2}}{m+n})\]
点Qの座標
\[\displaystyle (\frac{-nx_{1}+mx_{2}}{m-n},\frac{-ny_{1}+my_{2}}{m-n})\]
[/st-midasibox]
本記事では、内分点・外分点の公式や証明,求め方を単元別で解説します。
この記事を読むことで、内分点・外分点の座標が求められるようになります。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
内分点・外分点とは

そもそも内分点・外分点ってなんなの?ってところから解説します。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
内分点とは
線分を\(m:n\)になるように線分の内側で分ける点
外分点とは
線分が\(m:n\)になるように線分の外側にある点
[/st-mybox]
下の図のように線分を内側で分ける点を内分点といいます。
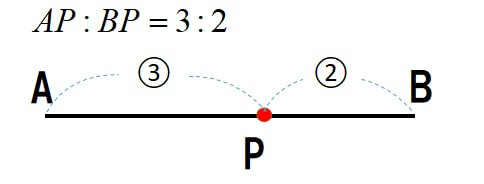
一方で、線分がある比になるように線分の外側に定まる点を外分点といいます。
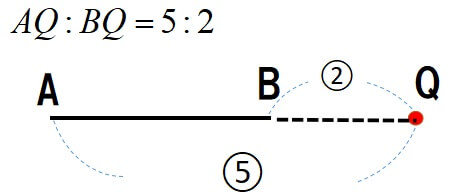
 高校生
高校生内側で分けるのが内分点で外側で分けるのが外分点だね!
数直線の内分点・外分点
数直線の内分点・外分点について解説します。
数直線を分ける
まずは、数直線上に異なる2点\(A(a),B(b)\)がある場合を考えます。
この場合、A,Bの並び方は下の図のように2通りの並べ方があります。
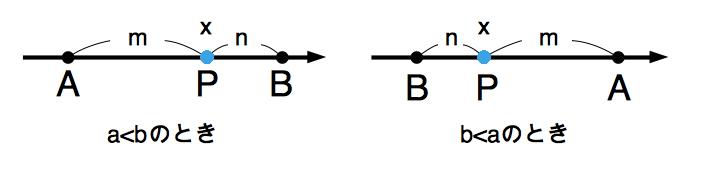
いずれの場合においても次の公式が成り立ちます。
[st-midasibox title=”数直線上の内分点・外分点” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold” myclass=””]
数直線上の2点\(A(a),B(b)\)について、線分ABを\(m:n\)に内分する点をP、\(m:n\)に外分する点をQとすると、
点Pの座標 \(\displaystyle \frac{na+mb}{m+n}\)
点Qの座標 \(\displaystyle \frac{-na+mb}{m-n}\)
[/st-midasibox]
この公式が成り立つことを具体的な数字で確かめてみましょう。
内分点について
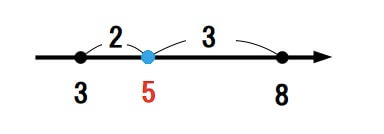
数直線上に異なる2点\(A(3)B(8)\)があります。この線分\(AB\)を\(2:3\)に内分する点Pの位置を求めます。
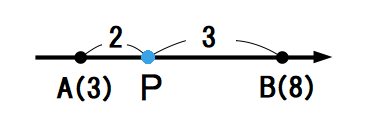
数直線上における内分点の公式に2点\(A,B\)の値と、内分する比\(m:n=2:3\)を代入します。
\[\displaystyle \frac{na+mb}{m+n}=\frac{3 \cdot 3 + 2 \cdot 8}{2+3}=\frac{25}{5}=5\]
したがって、線分ABを\(2:3\)に内分する点は\(P(5)\)だと分かりました。
実際に数直線で確かめてみると、5の点が線分ABを\(2:3\)に内分していることが分かります。
外分点について
つぎは外分点の公式に数字を代入してみます。
数直線上に異なる2点\(A(4)B(7)\)があります。この線分\(AB\)を\(2:1\)に外分する点Qの位置を求めましょう。
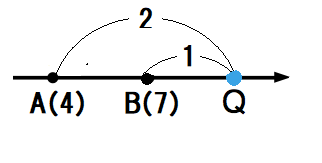
数直線上における外分点の公式に2点\(A,B\)の値と、外分する比\(m:n=2:1\)を代入します。
外分点を求めるときは\(-n\)を掛けることに注意しましょう。
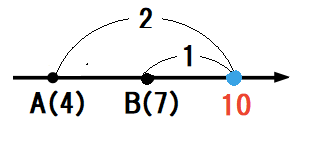
\[\displaystyle \frac{-na+mb}{m-n}=\frac{-1 \cdot 4 + 2 \cdot 7}{2-1}=10\]
したがって、線分ABを\(2:1\)に外分する点は\(Q(5)\)だと分かりました。
実際に数直線上で確かめてみると以下のようになります。
コンパスを使って作図
数直線上の内分点・外分点の見つけ方はもう1つあります。
コンパスを使うことで内分点・外分点を作図することができるのです。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#E8EAF6″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]
- 半直線ACを引く
- AC上に等間隔の\((m+n)\)個の点を作図
- 点Bと結ぶ
- 平行線を引く
[/st-mybox]
コンパスを使って内分点を作図する手順を解説します。
[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
人気教育系Youtuberの葉一さんが動画で作図の仕方を解説しています。
「【数学A】内分点・外分点の作図」
[/st-mybox]
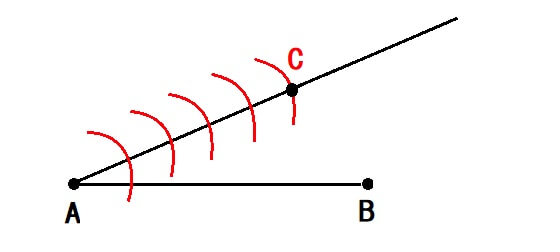
線分ABを\(3:2\)に内分する点を作図します。
まず、直線AB上にない点Cを適当に決めて半直線ACを引きます。
※半直線とは、片方を端として、もう一方が延々と伸びるまっすぐな線です。
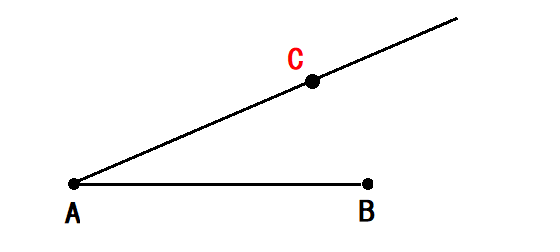
次にコンパスを使って線分ACを\((m+n)\)等分します。
今回は\(3:2\)に内分する点なので、線分ACを5等分します。
コンパスを適当な長さに開き、針を点Aに指して線を引きます。
いま引いた弧と直線ACの交点に針を刺し直して、あと4回繰り返します。
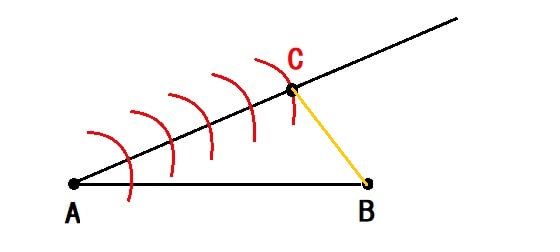
5回目に引いた線と半直線ACとの交点を点Bと結びます。
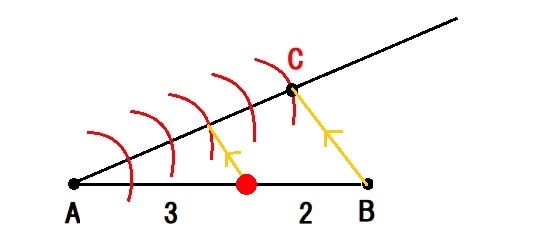
さいごに半直線AC上の\(3:2\)に内分している点から、平行線を引いて線分ABと交わった点が線分ABを\(3:2\)に内分する点です。
座標平面の内分点・外分点
座標平面上における内分点・外分点について解説します。
公式を紹介したあとに具体的な数字をいれて、内分点・外分点を見つける練習をしましょう。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
 高校生
高校生内分・外分の公式が覚えられなくて…
座標平面のときの公式
座標平面上における内分点・外分点について次の公式が成り立ちます。
[st-midasibox title=”座標平面の内分点・外分点” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold” myclass=””]
座標平面上の2点\(A(x_{1},y_{1}),B(x_{2},y_{2})\)について、線分ABを\(m:n\)に内分する点をP、\(m:n\)に外分する点をQとすると、
点Pの座標
\[\displaystyle (\frac{nx_{1}+mx_{2}}{m+n},\frac{ny_{1}+my_{2}}{m+n})\]
点Qの座標
\[\displaystyle (\frac{-nx_{1}+mx_{2}}{m-n},\frac{-ny_{1}+my_{2}}{m-n})\]
[/st-midasibox]
公式の証明
内分点・外分点の座標公式は中学校までの知識で証明できます。

座標平面上において2点A,Bと、線分ABを\(m:n\)に内分する点Pが存在するとき、
\(AP:PB=m:n\)ならば、\(A’P’:P’B’=m:n\)となります。(参考:平行線と比について確かめる)
したがって、
\begin{eqnarray}
(x-x_{A}):(x_{B}-x)&=&m:n\\
n(x-x_{A})&=&m(x_{B}-x)\\
nx-nx_{A}&=&mx_{B}-mx\\
mx+nx &=& nx_{A}+mx_{B}\\
\left( m+n \right)x&=&nx_{A}+mx_{B}
\end{eqnarray}
よって、
\[x=\dfrac{nx_{A}+mx_{B}}{m+n}\]
これで内分点Pの\(x\)座標がわかりました。同様にy座標も求めることができて証明終了です。
外分点も同じような考え方で証明します。
今回は\(m\)>\(n\)のときを証明しますが、\(m\)<\(n\)のときも同じように証明ができます。

\(AQ:QB=m:n\)のとき、\(A’Q’:Q’B’=m:n\)
したがって、
\begin{eqnarray}
(x-x_{A}):(x-x_{B})&=&m:n\\
n(x-x_{A})&=&m(x-x_{B})\\
nx-nx_{A}&=&mx-mx_{B}\\
mx-nx&=&-nx_{A}+mx_{B}\\
(m-n)x&=&-nx_{A}+mx_{B}
\end{eqnarray}
したがって、
\[x=\dfrac{-nx_{A}+mx_{B}}{m-n}\]
外分点Qの\(x\)座標を求めることができました。y座標についても同様に示して証明終了です。
実際に求めてみる
実際に内分点・外分点を座標公式を使って求めてみましょう。
内分点の座標
2点\(A(3,2),B(9,6)\)のとき、線分ABを\(3:2\)に内分する点Pの座標を求めます。
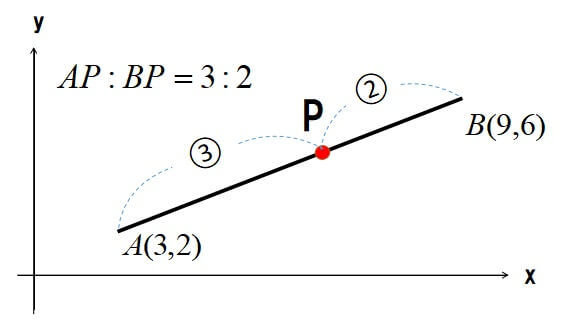
ポイントは分母は比の足し算、分子は両端の座標に比をクロスして掛けることです。
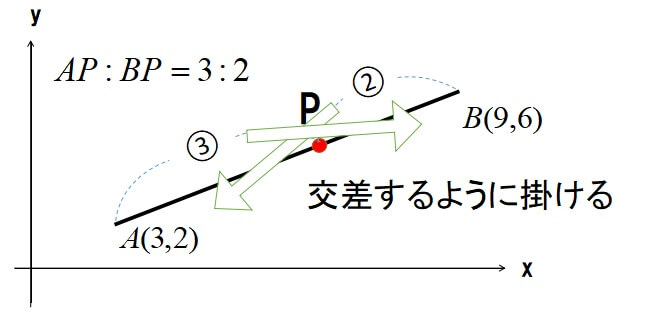
\(A(3,2),B(9,6)\)なので、
\[x_{P}=\displaystyle \frac{2\times{3}+3\times{9}}{3+2}=\displaystyle \frac{33}{5}\]
\[y_{P}=\displaystyle \frac{2\times{2}+3\times{6}}{3+2}=\displaystyle \frac{22}{5}\]
線分ABを\(3:2\)に内分する点Pの座標は、\(P\biggl(\displaystyle \frac{33}{5},\displaystyle \frac{22}{5}\biggr)\)
外分点の座標
つぎは座標公式を使って外分点を求めます。
2点\(A(3,2),B(9,6)\)のとき、線分ABを\(5:2\)に内分する点Qの座標を求めよ。
[st-cmemo myclass=”st-text-guide st-text-guide-attention” fontawesome=”fa-exclamation-circle” iconcolor=”#ef5350″ bgcolor=”#ffebee” color=”#000000″ bordercolor=”#ffcdd2″ borderwidth=”” iconsize=””]内分点の分母は比率を足しましたが、外分点では引き算をします。[/st-cmemo]
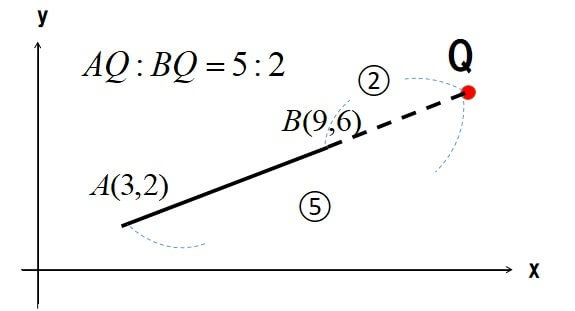
\(A(3,2),B(9,6)\)なので、
\[x_{P}=\displaystyle \frac{-2\times{3}+5\times{9}}{5-2}=\displaystyle \frac{39}{3}=13\]
\[y_{P}=\displaystyle \frac{-2\times{2}+5\times{6}}{5-2}=\displaystyle \frac{26}{3}\]
線分ABを\(5:2\)に内分する点Qの座標は、\(Q\biggl(13,\displaystyle \frac{26}{3}\biggr)\)
[st-mybox title=”ガイドメニュー” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
ベクトルの内分点・外分点
ベクトルにおける内分点・外分点の位置ベクトルについて解説します。
公式を解説したあとに、内分点・外分点の位置ベクトルを求める練習をしましょう。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
 高校生
高校生ベクトルの計算が苦手なんですよ…
位置ベクトルにおける公式
ベクトルにおける内分点・外分点の位置ベクトルは次の公式で求めます。
この公式は平面ベクトル、空間ベクトルどちらでも使えるので是非覚えておきましょう。
[st-midasibox title=”内分点・外分点の位置ベクトル” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold” myclass=””]
2点\(A(\vec{a}),B(\vec{b})\)を結ぶ線分ABを\(m:n\)に内分する点P、\(m:n\)に外分する点Qのそれぞれの位置ベクトルを\(\vec{p},\vec{q}\)とすると、
\(\displaystyle \vec{p}=\frac{n \vec{a} + m \vec{b}}{m+n}\)
\(\displaystyle \vec{q}=\frac{-n \vec{a} + m \vec{b}}{m-n}\)
[/st-midasibox]
公式の証明
内分点・外分点の位置ベクトル公式の証明は座標平面のときとは異なります。
内分点の位置ベクトル 証明
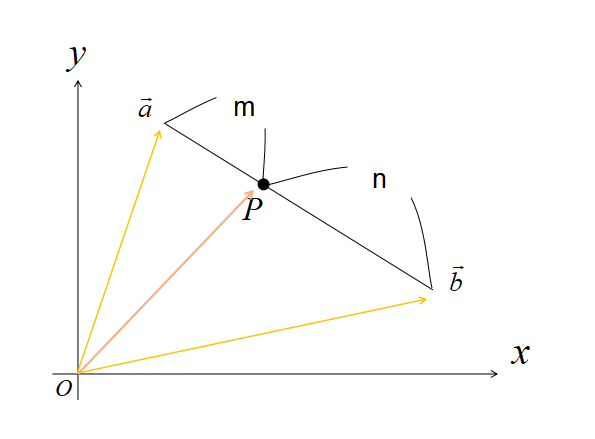
2点\(A(\vec{a}),B(\vec{b})\)を結ぶ線分ABにおいて、\(m:n\)に内分する点をPとする。
このとき点Pの位置ベクトル\(\vec{AP}\)は、
\(\displaystyle \vec{AP}=\frac{m}{m+n} \vec{AB}\)
ゆえに
\(\displaystyle \vec{p}-\vec{a}=\frac{m}{m+n}(\vec{b}-\vec{a})\)
よって
\(\displaystyle \vec{p}=(1-\frac{m}{m+n})\vec{a}+\frac{m}{m+n}\vec{b}\)
したがって
\(\displaystyle \vec{p}=\frac{n \vec{a} + m \vec{b}}{m+n}\)
外分点の位置ベクトル 証明
外分点も同じような考え方で証明します。
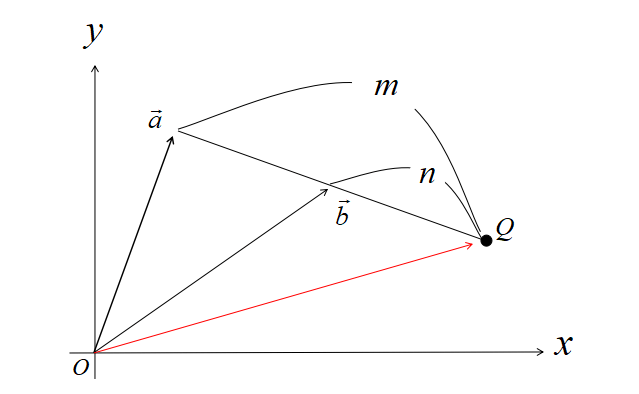
\(m > n\)のとき、2点\(A(\vec{a}),B(\vec{b})\)を結ぶ線分ABにおいて、\(m:n\)に外分する点をQとする。
このとき\(\vec{AQ}\)は、
\(\displaystyle \vec{AQ}=\frac{m}{m-n} \vec{AB}\)
ゆえに
\(\displaystyle \vec{q}-\vec{a}=\frac{m}{m-n}(\vec{b}-\vec{a})\)
よって
\(\displaystyle \vec{q}=(1-\frac{m}{m-n})\vec{a}+\frac{m}{m-n}\vec{b}\)
したがって
\(\displaystyle \vec{q}=\frac{-n \vec{a} + m \vec{b}}{m-n}\)
\(m < n\)のとき\(\vec{AQ}\)は、
\(\displaystyle \vec{AQ}=\frac{m}{n-m} \vec{BA}=\frac{m}{m-n} \vec{AB}\)
ゆえに、\(m>n\)のときと同様に示される。
したがって、
\(\displaystyle \vec{q}=\frac{-n \vec{a} + m \vec{b}}{m-n}\)
実際に求めてみる
実際に平面ベクトルにおける内分点・外分点の位置ベクトルを求めましょう。
内分点の位置ベクトル
2点A,Bの位置ベクトルが\(\vec{a}=(2,6),\vec{b}=(10,2)\)のとき、線分ABを\(3:5\)に内分する点Pの座標を求めます。
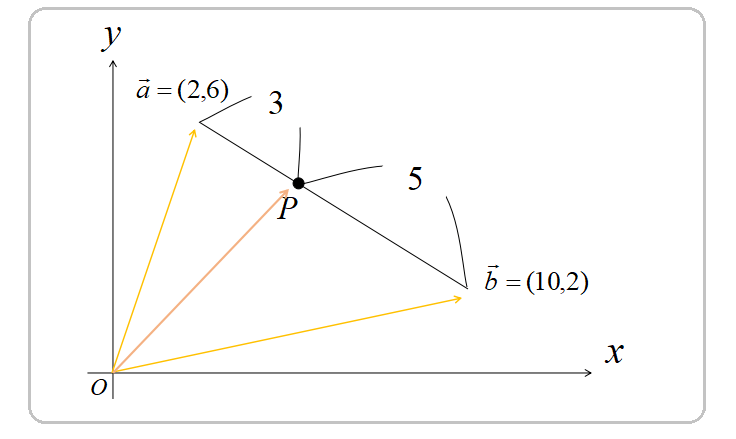
\(\vec{a}=(2,6),\vec{b}=(10,2)\)なので、点Pの位置ベクトル\(\vec{p}\)は
\begin{eqnarray}
\displaystyle \vec{p}&=&\frac{5\vec{a}+3\vec{b}}{3+5}\\
\displaystyle&=&\frac{5}{8}\vec{a}+\frac{3}{8}\vec{b}\\
\displaystyle&=&\frac{5}{8}(2,6)+\frac{3}{8}(10,2)\\
\displaystyle&=&(\frac{10}{8}+\frac{30}{8},\frac{30}{8}+\frac{6}{8})
\end{eqnarray}
したがって点Pの位置ベクトルは、
\(\displaystyle \vec{p}= (5,\frac{9}{2})\)
外分点の位置ベクトル
つぎは外分点の位置ベクトルを求めます。
2点A,Bの位置ベクトルが\(\vec{a}=(2,5),\vec{b}=(5,4)\)のとき、線分ABを\(2:1\)に外分する点Qの座標を求めます。
[st-cmemo myclass=”st-text-guide st-text-guide-attention” fontawesome=”fa-exclamation-circle” iconcolor=”#ef5350″ bgcolor=”#ffebee” color=”#000000″ bordercolor=”#ffcdd2″ borderwidth=”” iconsize=””]内分点の分母は比率を足しましたが、外分点では引き算をします。[/st-cmemo]
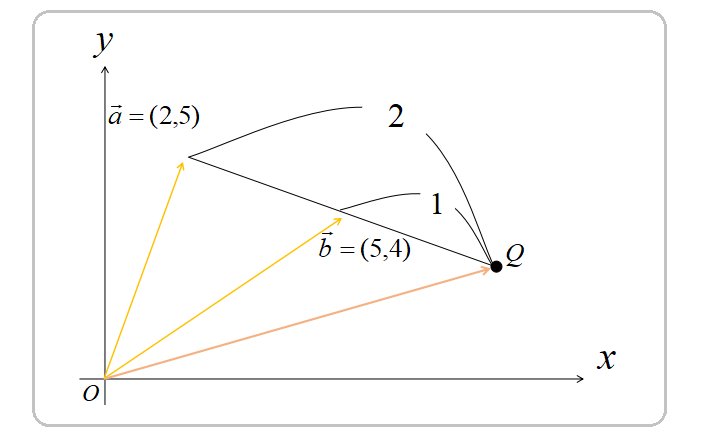
\(\vec{a}=(2,5),\vec{b}=(5,4)\)なので、点Qの位置ベクトル\(\vec{q}\)は
\begin{eqnarray}
\displaystyle \vec{q}&=& \frac{-\vec{a}+2\vec{b}}{2-1}\\
\displaystyle&=&-\vec{a}+2\vec{b}\\
\displaystyle&=&-(2,5)+2(5,4)\\
\displaystyle&=&(-2+10,-5+8)
\end{eqnarray}
したがって点Qの位置ベクトルは、
\(\displaystyle \vec{q}= (8,3)\)
これで平面ベクトルの内分点・外分点の位置ベクトルを求めることができました。
複素数平面の内分点・外分点
複素数平面上における内分点・外分点について解説します。
公式を紹介したあとに、内分点・外分点を求める練習をします。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
 高校生
高校生複素数の内分・外分がイメージできなくて…
複素数のときの公式
複素数平面上における内分点・外分点について次の公式が成り立ちます。
[st-midasibox title=”複素数平面の内分点・外分点” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold” myclass=””]
複素数平面上の異なる2点\(A{α},B{β}\)について、線分\(AB\)を\(m:n\)に内分する点をP、\(m:n\)に外分する点をQとすると、
点Pの座標
\[\dfrac{nα+mβ}{m+n}\]
点Qの座標
\[\dfrac{-nα+mβ}{m-n}\]
[/st-midasibox]
公式の証明
複素数平面における内分点・外分点の公式はベクトルに近い考え方で証明します。
複素数平面の内分点 証明

2点\(A(α),B(β)\)を結ぶ線分\(AB\)において、\(m:n\)に内分する点をPとする。
このとき点Pを表す複素数は、
\(\displaystyle z=α+ \frac{m}{m+n}(β-α)\)
ゆえに
\(\displaystyle z=(1-\frac{m}{m+n})α+ \frac{m}{m+n}β\)
したがって
\(\displaystyle z=\frac{nα+mβ}{m+n}\)
複素数平面の外分点 証明
外分点も同じような考え方で証明します。

\(m > n\)のとき、複素数平面上の2点\(A(α),B(β)\)を結ぶ線分ABにおいて、\(m:n\)に外分する点をQとする。
このとき点Qを表す複素数は、
\(\displaystyle z=α+ \frac{m}{m-n}(β-α)\)
ゆえに
\(\displaystyle z=(1-\frac{m}{m-n})α+ \frac{m}{m-n}β\)
したがって
\(\displaystyle z=\frac{-nα+mβ}{m-n}\)
\(m < n\)のとき点Qの複素数は、
\(\displaystyle z=α+ \frac{m}{m-n}(β-α))\)
ゆえに、
\(\displaystyle z=(1-\frac{m}{m-n}α+ \frac{m}{m-n}β\)
したがって、
\(\displaystyle z=\frac{-nα+mβ}{m-n}\)
実際に求めてみる
実際に複素数平面上の内分点・外分点を求めてみましょう。
内分点の複素数
複数平面上の2点\(A(α)=3+2i,B(β)=9+6i\)のとき、線分ABを\(3:2\)に内分する点Pを表す複素数を求めます。

ABを\(3:2\)に内分するので
\(\displaystyle z=\frac{2α+3β}{3+2}\)
\(A(α)=3+2i,B(β)=9+6i\)より
\(\displaystyle z=\frac{2(3+2i)+3(9+6i)}{5}\)
よって
\(\displaystyle z=\frac{33+22i}{5}\)
線分ABを\(3:2\)に内分する点Pを表す複素数は
\(\displaystyle z=\frac{33+22i}{5}\)
外分点の複素数
つぎは外分点の複素数を求めます。
複数平面上の2点\(A(α)=3+2i,B(β)=9+6i\)のとき、線分ABを\(5:2\)に外分する点Qを表す複素数を求めます。
[st-cmemo myclass=”st-text-guide st-text-guide-attention” fontawesome=”fa-exclamation-circle” iconcolor=”#ef5350″ bgcolor=”#ffebee” color=”#000000″ bordercolor=”#ffcdd2″ borderwidth=”” iconsize=””]内分点の分母は比率を足しましたが、外分点では引き算をします。[/st-cmemo]

ABを\(5:2\)に外分するので
\(\displaystyle z=\frac{-2α+5β}{5-2}\)
\(A(α)=3+2i,B(β)=9+6i)より
\(\displaystyle z=\frac{-2(3+2i)+5(9+6i)}{3}\)
よって
\(\displaystyle z=\frac{39+26i}{3}\)
線分ABを\(5:2\)に外分する点Qを表す複素数は
\(\displaystyle z=13+\frac{26}{3}i\)
これで複素数平面上のの内分点・外分点を求めることができました。
よくある間違い

内分点・外分点を求めるときに気を付けることをまとめました。
[st-cmemo fontawesome=”fa-exclamation-circle” iconcolor=”#ef5350″ bgcolor=”#ffebee” color=”#000000″ iconsize=”200″]
- \(x\)と\(y\)は別で考える
- 比はクロスして掛ける
- 外分点の\(-n\)に注意
[/st-cmemo]
xとyは一緒に計算することはない
内分点・外分点を求めるとき、\(x\)と\(y\)を一緒に計算することはないです。
よくある間違えとしてこんなミスをします。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#ffebee” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]\[\displaystyle (\frac{nx_{1}+my_{1}}{m+n},\frac{nx_{2}+my_{2}}{m+n})\][/st-mybox]
どこが違うか分かりますか?
正しい内分点の座標公式はこちらです。
\(\displaystyle (\frac{nx_{1}+mx_{2}}{m+n},\frac{ny_{1}+my_{2}}{m+n})\)
\(x\)座標は2点の\(x\)同士で計算して、\(y\)座標も\(y\)同士で計算するのが正解です。
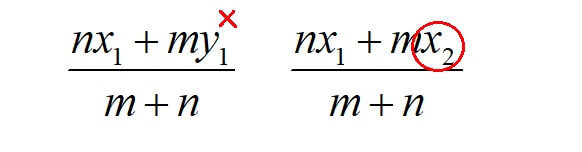
比はクロスして掛ける
内分点・外分点の座標を求めるとき、分子には比をクロスして掛けることに注意してください。
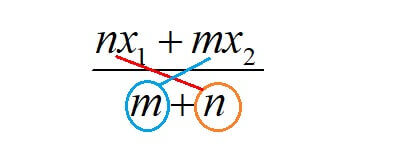
外分点の-nに注意
外分点の座標は、\(n\)ではなく\(-n\)を掛けることを忘れないでください。
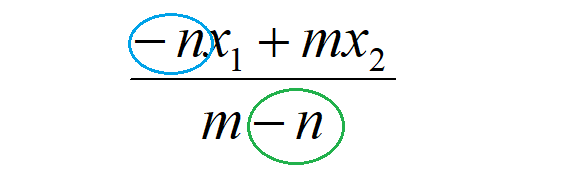
[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#fafafa” align=”” add_style=”margin-bottom:0px; border-top:2px #ccc solid; border-bottom:2px #ccc solid;”]
基礎から丁寧に確認!
プロ講師の分かりやすい解説
[/st-wide-background]
[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#ffffff” align=”” add_style=””]
ここまで読んで、まだピンと来ていない人いますか?
もしかすると、あなたには文章よりも動画解説のほうが合っているかもしれません。

河合塾が提供する「河合塾One」なら解説が丁寧で、基礎から確認できるのでおすすめです。
しかも、いまなら無料体験で全授業が視聴できます。
[/st-wide-background]
内分点・外分点 まとめ
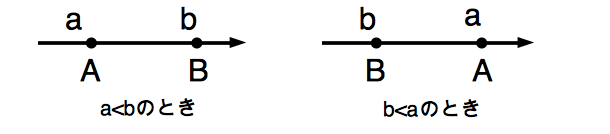
今回は内分点と外分点について、さまざまな単元の解説しました。
ベクトルも複素数も考え方は座標平面の内分点・外分点の公式とおなじです。
[st-midasibox title=”座標平面の内分点・外分点” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold” myclass=””]
座標平面上の2点\(A(x_{1},y_{1}),B(x_{2},y_{2})\)について、線分ABを\(m:n\)に内分する点をP、\(m:n\)に外分する点をQとすると、
点Pの座標
\[\displaystyle (\frac{nx_{1}+mx_{2}}{m+n},\frac{ny_{1}+my_{2}}{m+n})\]
点Qの座標
\[\frac{-nx_{1}+mx_{2}}{m-n},\frac{-ny_{1}+my_{2}}{m-n})\]
[/st-midasibox]
内分点は比率の和で、外分点は比率の差になので注意してください。
また、分子は分母の項をクロスで掛けるのも重要なポイントです。
内分点・外分点の公式を覚えてしまえば、それぞれの座標も簡単に求めることができます。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
座標上の2点を結ぶ距離も求められるようにしましょう。
[/st-mybox]

