ユークリッドの互除法のやり方と証明を分かりやすく解説！

「ユークリッドの互除法のやり方が分からない」
「1次不定方程式が苦手」
今回はユークリッドの互除法に関する悩みを解決します。

ユークリッドの互除法は、2つの整数の最大公約数を求めるときに使います。

最大公約数の求め方は非常に簡単です。

2379と3355の最大公約数を求めるとき

ユークリッドの互除法では

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#ffebee” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]「700と315の最大公約数」

＝「315と70の最大公約数」

＝「70と35の最大公約数」

[/st-mybox]

という考え方を用いて計算しています。

本記事では、ユークリッドの互除法のやり方や証明について解説しています。

ユークリッドの互除法の詳しい手順や1次不定方程式の応用についても解説しているので、ぜひ最後まで読んでください。

ユークリッドの互除法とは？

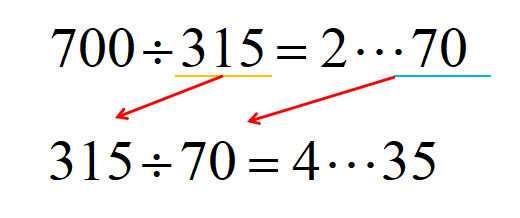
ユークリッドの互除法は、2つの整数の最大公約数を求める計算方法です。

[st-mybox title=”最大公約数とは？” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

2つ以上の整数のそれぞれの約数のうち、共通の約数を公約数といいます。
公約数の中でも最大の公約数を、最大公約数といいます。

12の約数：1,2,3,4,6,12
18の約数：1,2,3,6,9,12

12と18の公約数：1,2,3,6

したがって、12と18の最大公約数は6

[/st-mybox]

ユークリッドの互除法のやり方

ユークリッドの互除法のやり方を解説します。

315と700の最大公約数を求めるとします。

まずは大きい方の整数を小さい整数で割ります。

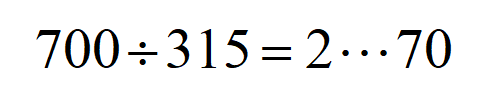
ここで求めた余りを使って次の計算をします。

割る数と余りを左にズラして、もう一度割り算を行います。

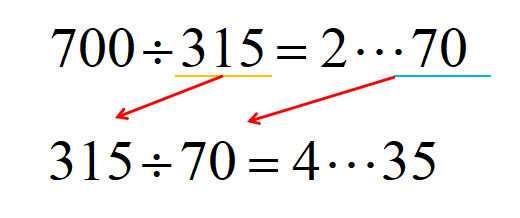
するとまた余りが出てきました。

これを余りが出なくなるまで繰り返します。

70を35で割ったところで商が2となり、余りが無くなりました。

したがって、315と700の最大公約数は35となります。

ユークリッドの互除法の具体例

ユークリッドの互除法に慣れるためにもう1問解いてみましょう。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

3355と2379の最大公約数を求めましょう。

[/st-mybox]

まずは3355を2379で割って余りを求めることから始めます。

割る数を余りでもう一度割る作業を繰り返していき、余りが出なくなったところで計算終了です。

したがって、3355と2379の最大公約数は61だと分かりました。

最大公約数の記号

最大公約数を表す記号があります。

「3355と2379の最大公約数」と毎回書くのは大変なので、知っておくと便利です。

[st-mybox title=”最大公約数の記号” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

3355と2379の最大公約数は61 ⇔　\(gcd(3355,2379)=61\)

[/st-mybox]

最大公約数は\(gcd(x,y)\)を用いて表します。

ユークリッドの互除法のメリット

12と18なら、約数をすべて書き出して最大公約数を求めることも可能です。

しかし、

[st-mybox title=”問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

31869169と472749749の最大公約数を求めよ

[/st-mybox]

こうなると約数をすべて書き出すのは不可能に近いです。

ユークリッドの互除法は、大きな数の最大公約数を求めるときに便利です。

とはいえ、入試問題でこんなに大きな整数はほとんど登場しないです。

大学入試においては最大公約数を求める問題よりも，一次不定方程式 ax+by=1 の問題でユークリッドの互除法を活用します。

ユークリッドの互除法の証明

ユークリッドの互除法では、

「割られる数と割る数の最大公約数」＝「割る数とあまりの最大公約数」

という考え方を用いて最大公約数を求めます。

つまり以下の計算では、

「700と315の最大公約数」
＝「315と70の最大公約数」
＝「70と35の最大公約数」

となるので、700と315の最大公約数が35だといえるのです。

ここで、なぜ「700と315の最大公約数」＝「70と35の最大公約数」が成り立つのか疑問を抱く学生も多いでしょう。

そんなあなたに向けて、ユークリッドの互除法の証明を示します。

まずは以下のことを証明します。

[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

2つの整数\(a,b(a≥b>0)\)についてaをbで割った余りをrとするとき、aとbの最大公約数はbとrの最大公約数と等しい

[/st-mybox]

《証明》

aとbの最大公約数をGとすると、
\(a=Ga’,b=Gb’ (a’とb’は互いに素) \cdots ①\)
と書ける。

\(a=bQ+r \cdots ②\)

②に①を代入して整理すると
\(G(a’-Qb’)=r\)

\(a’-Qb’=r’\)と置くと
\(r=Gr’\)

よってbとrはGを公約数に持つ。
また、②よりbとrはGより大きな公約数を持たないのでbとrの最大公約数はGである。

これで証明終了です。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

2つの整数\(a,b(a≥b>0)\)についてaをbで割った余りをrとするとき、aとbの最大公約数はbとrの最大公約数と等しい

[/st-mybox]

これは

「割られる数と割る数の最大公約数」＝「割る数とあまりの最大公約数」

を意味します。

つまり、「割り切れるまでユークリッドの互除法を続けたときの最後の割る数が最大公約数である」ということが言えるのです。

したがって、

[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

「700と315の最大公約数」
＝「315と70の最大公約数」
＝「70と35の最大公約数」

[/st-mybox]

となり、700と315の最大公約数が35となります。

ユークリッドの互除法と不定方程式

ここまでユークリッドの互除法を解説しましたが、大学入試で最大公約数を求めるだけの問題はほとんどありません。

入試においてユークリッドの互除法が一番活躍するのは「1次不定方程式」の問題への利用です。

一次不定方程式の基礎を確認

1次不定方程式では次のような問題が出ます。

[st-mybox title=”1次不定方程式の問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(2x+3y=1\)を満たす整数解をすべて求めよ。

[/st-mybox]

まずは方程式を満たす整数解を1つ見つけます。

これくらい小さい数字ならば、実際に数字を代入して整数解を見つけます。

\(2x-3y=1 \cdots ①\)

この方程式は\((x,y)=(2,1)\)で成り立つことが分かります。

\(2 \cdot 2 -3 \cdot 1=1 \cdots ②\)

\(①-②\)

\(2(x-2)-3(y-1)=0\)

これを変形すると

\(2(x-2)=3(y-1) \cdots ③\)

2と3は互いに素なので、\(x-2\)は3の倍数だと分かります。

よって、kを整数として、\(x−2=3k\)と表すことができます。

これを③に代入すると

\(2⋅3k=3(y-1)\)

\(∴　y-1=2k\)

したがって、求める解は

\(x=3k+2, y=2k+1（kは整数）\)⋯【答】

ユークリッドを用いて不定方程式を解く

1次不定方程式の解き方を解説しました。

[st-mybox title=”ユークリッドの応用” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の方程式を満たす整数解をすべて求めよ。

\(275x+61y=1\)

[/st-mybox]

ここでユークリッドの互除法が非常に活躍します。

まずは275と61でユークリッドの互除法を計算します。

余りが1になるまでユークリッドの互除法を繰り返します。

ここからは最大公約数を求めるときとは異なる手順なので注目です。

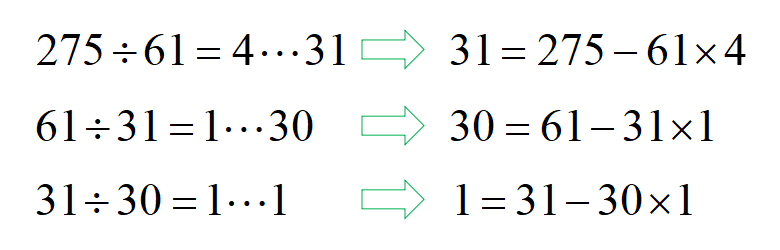
一番下の式に、上の式を順に代入していくと

\begin{aligned}
1 &=31-30 \cdot 1 \\
&=31-(61-31 \cdot 1) \cdot 1 \\
&=31 \cdot 2+61 \cdot(-1) \\
&=(275-61 \cdot 4) \cdot 2+61 \cdot(-1) \\
&=275 \cdot 2+61 \cdot(-9)
\end{aligned}

ゆえに、
\(275 \cdot 2+61 \cdot(-9)=1 \cdots ②\)

したがって、275x+61y=1の整数解の1つは x=2, y=−9 だとわかりました。

①－②より

\(275(x−2)+61(y+9)=0\)

\(∴　275(x−2)=−61(y+9) \cdots ③\)

275と61は互いに素だから、\(x−2\)は61の倍数といえます。

よって、kを整数として、\(x−2=61k\)と表すことができます。

これを③に代入すると

\(275⋅61k=−61(y+9)\)

\(∴　y+9=−275k\)

したがって、求める解は

\(x=61k+2, y=−275k−9（kは整数)\)

ユークリッドの互除法《練習問題》

ここまでユークリッドの互除法について解説してきました。

ユークリッドの互除法を活用して問題を解く練習をします。

[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

3465と7812の最大公約数を求めよ。

[/st-mybox]

次に1次不定方程式の整数解を求める問題も練習しましょう。

[st-mybox title=”練習問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の不定方程式を満たす整数解をすべて求めよ。

\(92x+197y=1\)

[/st-mybox]

[st-slidebox fontawesome=”” text=”+ 解答はここをクリック” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]

まずは\(92x+197y=1\)を満たす整数解の1つを見つけます。

\(92x+197y=1 \cdots　①\)

とする。

これらを式変形していくと

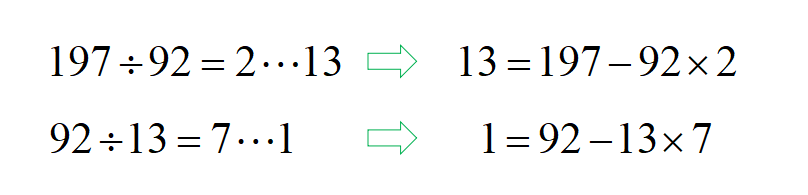
\(1 =92-13 \cdot 7\)
\(=92-(197-92 \cdot 2) \cdot 7\)
\(=92 \cdot (-13)-197 \cdot 7\)
\(=92 \cdot (-13)+197 \cdot(-7) \cdots ②\)

したがって、\((x,y)=(-13,-7)\)は①を満たす1つの整数解であることが分かりました。

\(92x+197y=1 \cdots　①\)
\(92 \cdot (-13)+197 \cdot(-7)=1 \cdots ②\)

①-②より

\(92(x+13)+197(y+7)=0\)

\(92(x+13)=-197(y+7) \cdots ③\)

ここで92と197は互いに素なので、x+13が197の倍数である。

よって、kを整数として、\(x+13=197k\)と表すことができます。

これを③に代入すると

\(92⋅197k=−197(y+7)\)

\(∴　y+7=−92k\)

したがって、求める解は

\(x=197k-13, y=−92k−7（kは整数）\)

[/st-slidebox]

ユークリッドの互除法　まとめ

今回はユークリッドの互除法についてまとめました。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#FFFDE7″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]

・ユークリッドの互除法は２つの整数の最大公約数を求める計算

・ユークリッドの互除法のやり方

・一次不定方程式で活躍

ユークリッドの互除法と1次不定方程式はここで解説しています。
⇒ユークリッドの互除法と1次不定方程式

[/st-mybox]

ユークリッドの互除法は計算が複雑なので、難しくて苦手というイメージを与えてしまいます。

実際には割る数と余りをズラしているだけなので、慌てずにじっくりと解説を読んで見てください。

どうしても整数の性質が苦手な方は参考書の丁寧な解説をおすすめします。

志田晶の 集合・論理、整数が面白いほどわかる本

Amazon kindleなら無料で参考書が読める！
[st-card myclass=”” id=”4376″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]