二重根号の外し方を解説！たったこれだけで簡単に外せる！

今回は数Ⅰの「数と式」から、二重根号についての悩みを解決していくよ！

こんにちは！数学講師のゆうやです！

高校生の勉強に関する相談に乗ったり、高校数学の解説記事を書いたりしています！

さて、今回は二重根号の外し方について考えていきましょう。

まずはこちらをご覧ください。

ルートの中にルートがあって、初めて見た人はビックリしますよね

二重根号は外し方は公式を知らないと、この後の計算に手も足も出ないです。

簡単な公式なので、この機会に必ず習得しておきましょう。

本記事では、”二重根号”の外し方について解説していきます。

2がないパターンや、マイナスの二重根号についても解説してるのでぜひ最後までご覧ください。

二重根号とは？

今回解説する”二重根号”というのは、ルートのなかにルートがあるものを指します。

\[\sqrt{5+2\sqrt{6}}、\sqrt{5-2\sqrt{6}}\]

二重根号の解説をする前に、「根号」について確認しましょう。

根号というと難しいですが、ルート\(\sqrt{　}\)のことを指しています。

根号の中身に文字が入っているときは、文字の符号によって場合分けが必要です。

二重根号の外し方

二重根号とは、ルートのなかにルートがあるものを指していました

\[\sqrt{5+2\sqrt{6}}、\sqrt{5-2\sqrt{6}}\]

このままでは計算が難しすぎますね。

以下の公式を使うことで、二重根号は2つのルートに形を変えることができます。

公式だけ見せられてもピンと来ないですよね。実際に、二重根号を外してみましょう。

まずは加法の形をした二重根号を外します。

この公式を思い出して、足して8、掛けて15になる数字の組み合わせを考えると、\(a=5,b=3\)の組がありますね。

よって、

\begin{eqnarray}
\sqrt{8+2\sqrt{15}}&=&\sqrt{(5+3)+2\sqrt{5\cdot 3}}\\
&=&\sqrt{5}+\sqrt{3}
\end{eqnarray}

これで二重根号を外すことができました。

同様の方法で、減法の形をした二重根号も外してみましょう。

この場合は、足して12、掛けて35になる数字の組み合わせを考えると、\(a=7,b=5\)の組がありますね。

よって、

\begin{eqnarray}
\sqrt{12-2\sqrt{35}}&=&\sqrt{(7+5)-2\sqrt{7 \cdot 5}}\\
&=&\sqrt{7}-\sqrt{5}
\end{eqnarray}

これで減法の二重根号も外すことができました。

二重根号の公式《証明》

二重根号の外し方の公式を証明しておきましょう。

なぜこの公式で二重根号を外すことができるのでしょうか。

証明

二重根号の外し方を証明するには、以下の展開の公式がポイントになります。

まずは加法の二重根号は、

\begin{eqnarray}
\sqrt{(a+b)+2\sqrt{ab}}&=&\sqrt{(\sqrt{a}+\sqrt{b})^{2}}\\
&=&|\sqrt{a}+\sqrt{b}|
\end{eqnarray}

となり、\(\sqrt{a}\)も\(\sqrt{b}\)も正の数なので

\[|\sqrt{a}+\sqrt{b}|=\sqrt{a}+\sqrt{b}\]

したがって、

\(a>0,b>0\)とすると

\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]

減法の二重根号も同様の証明をします。

\begin{eqnarray}
\sqrt{(a+b)-2\sqrt{ab}}&=&\sqrt{(\sqrt{a}-\sqrt{b})^{2}}\\
&=&|\sqrt{a}-\sqrt{b}|
\end{eqnarray}

\(a>b>0\)ならば、\(\sqrt{a}-\sqrt{b}>0\)が成り立つので、

\[|\sqrt{a}-\sqrt{b}|=\sqrt{a}-\sqrt{b}\]

したがって、\(a>b>0\)のとき

\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]

2がない二重根号の外し方

二重根号の計算には以下のようなものもあります。

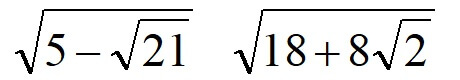
前半部分で紹介した二重根号とどこが異なるか分かりますか？

こういった二重根号を外すには工夫が必要です。

2を作るパターン

二重根号は足してAの部分、掛けてBの部分になる、\(a,b\)の組み合わせを探します。

しかし、このままだとBの根号の前に２がないので無理やり式変形をします。

\begin{eqnarray}
\displaystyle \sqrt{4+\sqrt{15}}&=&\sqrt{\frac{8+2\sqrt{15}}{2}}\\
\displaystyle &=&\frac {\sqrt{8+2\sqrt{15}}}{\sqrt{2}}\\
\displaystyle &=&\frac {\sqrt{3}+\sqrt{5}}{\sqrt{2}}\\
\displaystyle &=&\frac {\sqrt{6}+\sqrt{10}}{2}
\end{eqnarray}

これで二重根号を外すことができました。

2になるように調整するパターン

根号の係数が6なので、2になるように調整します。

\[\sqrt{14-6\sqrt{5}}=\sqrt{14-2\sqrt{45}}\]

こうなってしまえば、二重根号の公式に当てはめて、

足して14、掛けて45になる数の組み合わせは、\((a,b)=(9,5)\)

\begin{eqnarray}
\sqrt{14-6\sqrt{5}}&=&\sqrt{14-2\sqrt{45}}\\
&=&\sqrt{9}-\sqrt{5}\\
&=&3-\sqrt{5}
\end{eqnarray}

よって、二重根号を外すことができました。

二重根号を外す《練習問題》

二重根号の式を簡単にする問題を解いてみましょう。

(1)の解説

これは二重根号の公式がそのまま使えるパターンですね。

\begin{eqnarray}
\sqrt{7+2\sqrt{10}}&=&\sqrt{(5+2)+2\sqrt{5 \cdot 2}}\\
&=&\sqrt{5}+\sqrt{2}
\end{eqnarray}

(2)の解説

これは2がないので工夫が必要です。

\begin{eqnarray}
\displaystyle \sqrt{5+\sqrt{21}}&=&\sqrt{\frac{10+2\sqrt{21}}{2}}\\
\displaystyle &=&\frac{\sqrt{10+2\sqrt{21}}}{\sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{7}+\sqrt{3}}{\sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{14}+\sqrt{6}}{2}
\end{eqnarray}

(3)の解説

これは2をつくる工夫が必要です。

\begin{eqnarray}
\displaystyle \sqrt{18+8\sqrt{2}}&=&\sqrt{18+2\sqrt{32}}\\
\displaystyle &=&\sqrt{16}+\sqrt{2}\\
\displaystyle &=&4+\sqrt{2}\\
\end{eqnarray}

二重根号の外し方　まとめ

今回は二重根号の外し方についてまとめました。

二重根号は以下の公式を使うと、簡単な形に変えることができます。

公式は簡単なのでたくさん問題を解き、公式に慣れていきましょう。

三乗の公式について知りたい方はこちらの記事がおすすめです。

▼数学Ⅰ「数と式」の重要ポイントをまとめた記事を作りました。